Lezione 3

Flusso
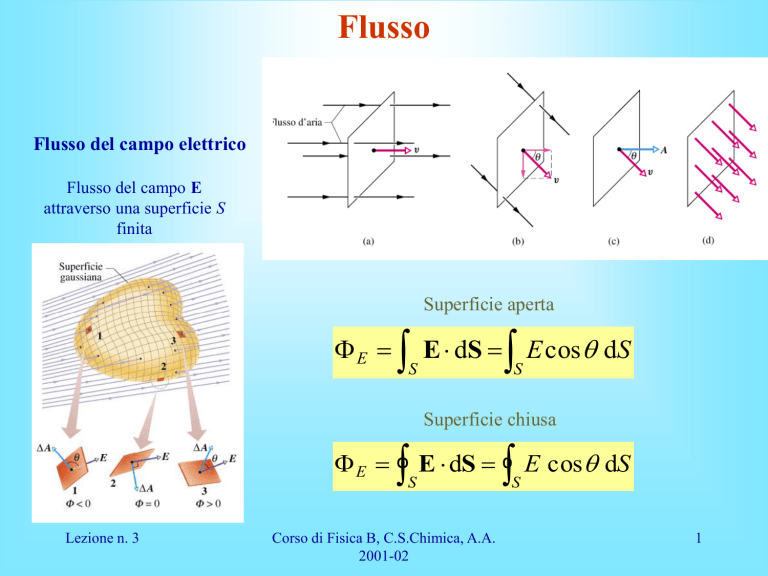
Flusso del campo elettrico
Flusso del campo E
attraverso una superficie S
finita
Superficie aperta
E 
 E dS   Ecos dS
S
S
Superficie chiusa
E 
Lezione n. 3
 E  dS   E cos dS
S
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
S
1
Il teorema di Gauss
Il flusso del vettore E campo elettrico attraverso una superficie chiusa S vale:
E 
Q

0

S
E  dS 
Q
0
Dove Q = somma di tutte le cariche interne alla superficie chiusa S.
NB: le cariche esterne NON contribuiscono al flusso
Q

qi
•
• •qi
i
Lezione n. 3
•
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
•
•
2
Analogie tra legge di Gauss e di Coulomb
Sono due modi diversi per enunciare lo stesso fenomeno fisico.
I due punti fondamentali sono:
1) La dipendenza della forza di Coulomb da 1/r2
2) L’additività dei campi (E, F)
• La legge di Coulomb permette di ottenere il campo E una volta nota la carica Q,
mentre con il teorema di Gauss, noto il campo E, si ottiene la carica presente in una
certa regione dello spazio.
• Mentre la legge di Coulomb cessa di valere per cariche in moto, il teorema di Gauss
si può applicare sia a cariche in quiete sia a cariche in moto. Il teorema di Gauss è
quindi più generale della legge di Coulomb.
Lezione n. 3
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
3
Esempio: campo elettrico di una carica
Come esempio, vogliamo calcolare il campo elettrico generato
da una carica q usando il teorema di Gauss
Superficie gaussiana = sfera di raggio r centrata in q
Il flusso vale:
 E  E S dS E4  r
Quindi:
Lezione n. 3
E
q

q
4  r  
Il teorema di Gauss dice che:
E
2
2
0
4  0 r 2
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
4
Conseguenze del teorema di Gauss
In un conduttore carico, in equilibrio elettrostatico,
la carica è distribuita sulla sua superficie
Infatti, in un conduttore carico in equilibrio
elettrostatico, le cariche sono in quiete
Inoltre, E = 0 (nei punti interni del conduttore)

Attraverso S (superficie gaussiana)  E = 0

Q = 0 (all’interno del conduttore)
Invece, vicino alla superficie di un conduttore
carico, la carica elettrica all’interno della
superficie gaussiana (cilindro) vale s S (dove s
= densità superficiale di carica locale e S è
l’area delle due superfici di base del cilindro).
Per il teorema di Gauss:
E  E S

Lezione n. 3

s
E
0
sS
ES
0
E
+
+
+
+
+
E=0
+
•P
S
+
+
+
+
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
+
+
5
Induzione elettrostatica
Carica inducente = +q
E = 0 (nei punti interni del conduttore)

Attraverso S (superficie gaussiana)
E = 0

Q = 0 (all’interno di S)

Carica indotta sulla superficie interna = -q
Carica indotta sulla superficie esterna = +q
NB: il risultato è INDIPENDENTE dalla posizione
della carica interna!!!
Ad esempio, se all’interno la somma delle cariche è
ZERO, il flusso è ZERO
Lezione n. 3
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
6
La gabbia di Faraday
Da quanto detto, risulta possibile creare uno schermo elettrostatico in un campo elettrico uniforme
(detto gabbia di Faraday) utilizzando come schermo un involucro metallico (schermo
elettrostatico)
Sono presenti cariche elettriche indotte sulla superficie esterna dello schermo
(La carica totale è nulla)

Il campo elettrico all’interno dello schermo è nullo
(Le linee di campo all’esterno sono modificate)

Lo schermo elettrostatico protegge dalle scariche elettriche
-
+
-
Lezione n. 3
E=0
-
+
+
+
+
+
+
+
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
7
Sistemi a simmetria cilindrica
Superficie gaussiana = cilindro di raggio r alto h centrato sulla
bacchetta
Il flusso vale:  E  EdS  E ( 2rh )

S
Il teorema di Gauss dice che: E ( 2rh )

Q
0
Quindi, usando la densità lineare di corrente, si ha:
Q

E

2rh 0 2 0 r
Lezione n. 3
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
8
Sistemi a simmetria piana: lastra carica
Superficie gaussiana = cilindro retto chiuso di
base A perpendicolare alla lastra
Il flusso vale:
 E   EdS  2 EA
S
2 EA 
Il teorema di Gauss dice che:
Q
0
Quindi, usando la densità superficiale di
corrente, si ha:
s
E
2 0
Lezione n. 3
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
9
Doppia piastra
Come nel caso precedente, si sceglie come superficie gaussiana un cilindro retto chiuso
di base A perpendicolare alla lastra. All’interno del cilindro la carica totale è nulla
(essendo le due densità di carica uguali ed opposte) per cui esternamente al doppio
strato E=0. Tra le due piastre, invece, si ha un contributo di campo elettrico E=s/20
diretto da sinistra a destra (perché uscente) dovuto alla piastra carica positivamente ed
un contributo di campo elettrico E=s/20 diretto ancora da sinistra a destra (perché
entrante) dovuto alla piastra carica negativamente. Per cui, il campo totale vale E=s/20
+ s/20 = s/0
Lezione n. 3
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
10
Sistemi a simmetria sferica
Per ogni superficie gaussiana esterna alla
distribuzione sferica, la carica totale
racchiusa al suo interno è q e pertanto il
campo
elettrico
esterno
risulta
indistinguibile da quello generato da una
carica puntiforme.
).
Per quanto riguarda il campo elettrico
interno, è importante sapere le caratteristiche
della distribuzione. Ad esempio, se essa è metallica, poiché le cariche in
un conduttore metallico sono distribuite soltanto sulla superficie, al suo
interno non ci sono cariche libere e quindi il campo elettrico è nullo. Nel
caso di una sfera isolante, invece, se la carica è distribuita al suo interno
in maniera uniforme (densità di carica r=dq/dV), è possibile valutare
dapprima la carica contenuta entro la superficie gaussiana (sfera di
3
r
r
raggio r<R):
4rr 3
r
q(r )   rdV  r  dV  rV (r ) 
 q 
3
 R
0
0
E quindi, essendo il flusso pari a:
E 
 E  dA   EdA  E  dA  EA(r )  4r E
q r
E
3
4

R
Si ottiene:
0
2
A( r )
Lezione n. 3
A( r )
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
A( r )
11