OTTICA
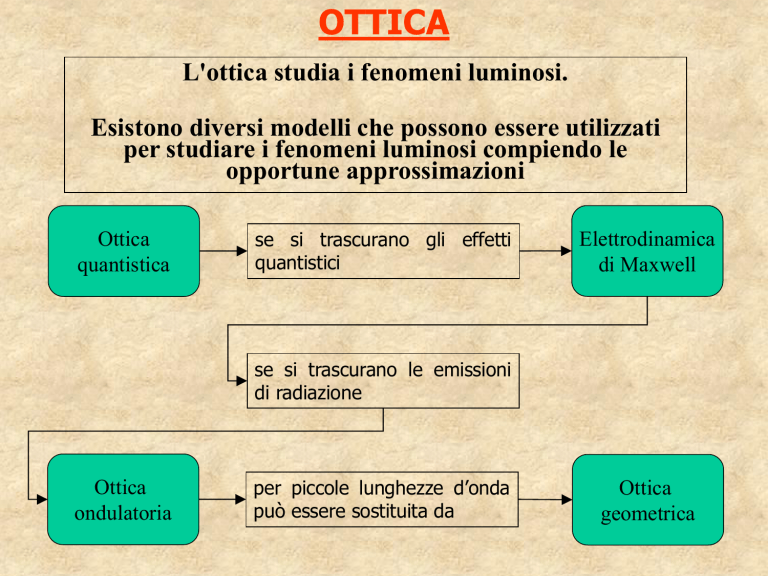
L'ottica studia i fenomeni luminosi.
Esistono diversi modelli che possono essere utilizzati
per studiare i fenomeni luminosi compiendo le
opportune approssimazioni
Ottica
quantistica
se si trascurano gli effetti
quantistici
Elettrodinamica
di Maxwell
se si trascurano le emissioni
di radiazione
Ottica
ondulatoria
per piccole lunghezze d’onda
può essere sostituita da
Ottica
geometrica
Ottica geometrica
•
•
•
•
I postulati dell'ottica geometrica
L'ottica geometrica si basa su quattro
postulati fondamentali:
propagazione rettilinea della luce;
indipendenza dei raggi luminosi;
riflessione della luce su una superficie
speculare;
rifrazione della luce sulla superficie di
separazione fra due mezzi trasparenti.
Le leggi dell’ Ottica geometrica
1.
Propagazione rettilinea della luce in un
mezzo omogeneo
Si rivela molto utile considerare i raggi luminosi come
delle semplici rette. Si tratta di un'astrazione matematica,
scelta per facilitare i ragionamenti e tale da permettere
una chiara rappresentazione dei fenomeni e dei
dispositivi sperimentali: le rette geometriche, a
differenza dei raggi luminosi, non hanno spessore.
2. Indipendenza dei raggi luminosi
Quando due o più raggi vengono a contatto non si
verifica alcuna alterazione della loro traiettoria o della
loro intensità.
Le leggi dell’ Ottica geometrica
3.
Riflessione della luce su una superficie speculare
raggio
incidente
ai
raggio
riflesso
ar
Il raggio incidente, il raggio riflesso e la
perpendicolare (normale) alla superficie
riflettente nel punto d'incidenza,
giacciono sul medesimo piano.
L'angolo di riflessione è uguale
all'angolo di incidenza: ai=ar. Se il
raggio incidente coincide con la normale
allo specchio, anche il raggio riflesso
forma un angolo di riflessione nullo:
coincide con il raggio incidente
(incidenza normale).
N.B. Queste leggi valgono anche se la superficie è curva. In questo caso la normale
nel punto d'incidenza è la perpendicolare al piano tangente alla superficie stessa in
quel punto. Quando la superficie è sferica la normale in un punto coincide con il
raggio della sfera (passante per quel punto)
Le leggi dell’ Ottica geometrica
4. Rifrazione della luce sulla superficie di separazione
fra due mezzi trasparenti.
Raggio incidente, raggio rifratto e normale nel
punto d'incidenza alla superficie di separazione dei
due mezzi giacciono sullo stesso piano.
Il rapporto tra i seni degli angoli che il raggio
incidente ed il raggio rifratto formano con la
normale è una costante che dipende dalla natura
dei due mezzi, dalle loro condizioni fisiche
(temperatura, pressione, stato di aggregazione) (e
dalla lunghezza d'onda della luce utilizzata). Tale
costante è denominata indice di rifrazione del
secondo mezzo rispetto al primo.
sin a I n2
n12
sin a R n1
raggio
incidente
aI
raggio
rifratto
aR
Le leggi dell’ Ottica geometrica
L'indice di rifrazione esprime il rapporto tra le
velocità assunte dalla luce in due mezzi come
una costante uguale al rapporto inverso dei
loro indici di rifrazione.
n2 v1
n1 v2
Se l'angolo di rifrazione è minore di quello di incidenza si dice che il secondo mezzo
(es. acqua) è più rifrangente del del primo (es. aria); se invece l'angolo di rifrazione è
maggiore di quello d'incidenza, il secondo mezzo è meno rifrangente del primo. In
generale i mezzi più densi sono anche più rifrangenti. Può tuttavia avvenire anche il
contrario: l'alcol, il petrolio, la benzina, pur essendo meno densi dell'aria sono più
rifrangenti di essa.
Le leggi della rifrazione, nella forma geometrica, si dicono anche leggi di Cartesio, perché
furono pubblicate per la prima volta da Descartes nel 1637, pur essendo state scoperte nel
1615 dall'olandese W. Snell.
Angolo limite e riflessione totale
Consideriamo il caso in cui il raggio
passa da un mezzo più rifrangente
ad un mezzo meno rifrangente.
n2 n1
Per un raggio incidente particolare e
l’angolo di rifrazione è di 90° cioè è
parallelo alla superficie.
L’angolo limite (critico), qC , è il valore dell’angolo d’incidenza
corrispondente. Per valori dell’angolo di incidenza maggiore non si ha
rifrazione (riflessione totale).
n2
n1 sin q C n2 sin
q C arcsin
2
n1
Riflessione totale : Le fibre ottiche
aria
n1
n2
sin θi sin θc
n1
quarzo
n = 1.45
vetro flint
n = 1.65
Rifrazione attraverso lastre
Viene denominato LASTRA un mezzo
trasparente delimitato da facce piane e
parallele.
Un raggio SI, incidendo obliquamente sulla lastra
MM', si rifrange secondo II'. Il raggio rifratto II'
forma con le normali n e n', tra loro parallele,
angoli interni uguali: r=r'. All'uscita nell'aria si
dovrà quindi verificare la condizione: i=i'.
Pertanto il raggio emergente I'S'
è parallelo al raggio incidente SI.
Un raggio che attraversa una lastra non è deviato
dalla sua direzione. Esso è spostato
parallelamente a se stesso: lo spostamento è
proporzionale allo spessore della lastra e
all'angolo d'incidenza.
Riflessione e rifrazione : un esempio
z
θi
50
θi'
50
sin θ'i sin θi
aria : n1 1.00
acqua : n2 1.33
θr
35.17
n1
sin θ r
sin θi
n2
Prisma ottico
Rifrazione attraverso superfici piane non parallele
Il prisma ottico è un mezzo rifrangente limitato da facce piane non
parallele formanti cioè un angolo diedro, detto "angolo del prisma".
Sia A l'angolo del prisma e SI un raggio incidente. Quando un raggio
proveniente dall'aria incide sul prisma (nel punto d'incidenza I), attraversa
un mezzo più rifrangente (vetro), quindi il raggio si avvicina alla normale
n1.
Quando poi giunge nel punto E emerge
dal prisma (a meno di superare l'angolo
limite) in un mezzo meno rifrangente,
l'aria, quindi il raggio si avvicina alla
normale n2 lungo la direzione ER. Per
effetto delle due rifrazioni il raggio
devia verso la base BC.
Prisma ottico
L'angolo
formato
dal
prolungamento del raggio emergente
EO con il prolungamento del raggio
incidente OF, è detto angolo di
deviazione del prisma.
Per ogni prisma vi è un angolo
minimo di deviazione: si ottiene
quando l'angolo d'incidenza e
l'angolo di uscita sono uguali.
Uno stesso materiale presenta indici di rifrazione diversi per i vari colori.
PROBLEMA NON RISOLTO
DALL’OTTICA GEOMETRICA
Il prisma devia con angoli
diversi raggi luminosi di
diverso colore
SORGENTI e IMMAGINI
Definizioni
fascio omocentrico
(coniugato) emergente
fascio omocentrico
incidente
S
sistema
ottico
oggetto
S’
immagine
punti coniugati
SORGENTI e IMMAGINI
Definizioni
reale
virtuale
oggetto
centro dei
raggi incidenti
centro del
prolungamento
dei raggi incidenti
immagine
centro dei
raggi emergenti
centro del
prolungamento
dei raggi emergenti
IMPORTANTE : La costruzione di una immagine può essere
fatta conoscendo i comportamento di 2 raggi.
SORGENTI e IMMAGINI
Definizioni
S
oggetto
reale
S’
immagine
reale
immagine
virtuale
S
S’
oggetto
reale
Specchio piano
Lo specchio piano è un sistema ottico semplice costituito da
un materiale che può riflettere i raggi luminosi.
specchio piano:
A’B’ è una immagine
virtuale e simmetrica
B
A
A’
B’
Specchio sferico concavo
C
R
O
h
centro
raggio
vertice
apertura lineare
P
R qq
’
S’
C a
asse ottico
S
superficie sferica
a
s
a’
s’
h
O
Specchio sferico convesso
superficie sferica
q
q
P
asse ottico
S
O ’ S’
R’’
a
a’’
s
a
C
Specchi sferici
R’’
R
S’
C
S
a’
a
O
s’
s
S
S’
O
s’’
s
C
a’’
a
1
1
2
s
s'
R
equazione degli specchi
Specchi sferici
se, nella:
1
1
s
s'
1
1
s'
2
prendiamo
R
R
2
s'
R
2
s
si ha:
distanza focale
f dello specchio
1
1
1
s
s'
f
R
R
C
O
F
C
O
F
Specchi sferici
Costruzione di immagini di oggetti estesi
P
y
y
F
y’
C
y’
O
O
s’
F
C
s
s
s’
L’ingrandimento laterale è definito (specchi concavi o convessi):
y'
s'
m
y
s
Esempi: lo specchio concavo
l’immagine è:
s>R
C
F
f<s<R
C
F
s<f
C
F
applicazioni
reale
rimpicciolita,
rovesciata
obiettivo
telescopio
reale
ingrandita,
rovesciata
obiettivo
proiettore
virtuale
ingrandita
specchio per
radersi, truccarsi
Esempi: lo specchio convesso
l’immagine è:
applicazioni
virtuale
rimpicciolita
specchietti
retrovisori
virtuale
rimpicciolita
specchietti
retrovisori
reale
ingrandita
oculare
cannocchiale
s>0
F
C
s>0
F
C
s<0
F
C
Diottro:rifrazione da superficie sferica
n1
qi
l
S
n2
P
R
O
D
s
qr
a
s’
diottro convesso
l’
S’
C
a
a’
asse ottico
superficie sferica
n1
n2
n2 n1
s
s'
R
equazione
del diottro
Diottro:rifrazione da superficie sferica
n1
P
a
S
S’
a’
n2 diottro concavo
R
O
C
a
s
s’
vale ancora:
n1
n2
n2 n1
s
s'
R
equazione
del diottro
Diottro:rifrazione da superficie sferica
n1
n2
s
s'
s'
n1
n2
n2 n1
f
R
n2
n1
n2 n1
R
F
con s f
in conclusione:
n1R
n2 n1
n1
n2
n2 n1
n1
n2 primario
fuoco
s
s'
R
f
f'
s
n1
n1
n2
n2 n1
f'
R
n2
F’
n2 R
con s ' f '
n2 n1
fuoco secondario
Oggetti estesi e costruzioni delle immagini
Tracciamento dei raggi con due dei tre raggi principali:
superficie convessa
n1
n2
P
F’
O
F
s
C
s’
immagine reale
Ingrandimento
y'
n1s '
m
y
n2 s
Oggetti estesi e costruzioni delle immagini
Tracciamento dei raggi con due raggi principali:
superficie concava
n1
P
n2
O
F’
C
s’
s
immagine virtuale
Ingrandimento
y'
n1s '
m
y
n2 s
F
Un diottro particolare: il piano
si consideri il caso:
n1
n2
s
s'
R
n1
S
P
S’
0
n2
n1
n2
S’
n2 n1
R
P
S
s
s
s’
n1 > n2 s > s’
s’
n1 < n2 s < s’
Esempi di diottro
acqua
n = 1.33
acqua
n = 1.33
h
la moneta “avvicinata”
la matita “spezzata”
LENTI
rifrazione e formazione dell’immagine da diottri successivi
n2
n1
n3
S2’= S3
S1
S3’
D1
D2
D3
n1
S1’= S2
LENTI
Combinazioni di più diottri: le lenti
LENTI semplici
Convergenti : 1) biconvessa, 2) piano-convessa, 3) concavo-convessa
Divergenti : 4) biconcava, 5) piano-concava, 6) convesso-concava
LENTI composte
LENTI : la teoria
t spessore della lente
n1
S’1 = S2
n2
S1
V1
-s’1
S’2
V2
n1
-s’1
s1
s’2
s2
t
per il primo diottro
1
n12
n12 1
1
s1
s '1
R1
f1
LENTI : la teoria
n1
n2
S’1 = S2
S1
V1
V2
n1
-s’1
s1
-s’1
s’2
s2
t
per il secondo diottro
n12
1
1 n12
1
s2
s '2
R2
f2 '
con:
s2 t s'1
S’2
LENTI : la teoria delle lenti sottili
t 0
s2 t s'1 s'1
Se la lente è sottile:
quindi:
S
possiamo sommare le due equazioni:
1
n12
n12 1
1
s1
s '1
R1
f1
n12
1
1 n12
1
s2
s '2
R2
f2 '
1
1
1
1
(n12 1)
s
s'
R2
R1
F’
O
F
S’
s
s’
equazione del
costruttore di lenti
LENTI : la teoria delle lenti sottili
1
1
1
1
(n12 1)
s
s'
R
R
2
1
equazione del costruttore di lenti
i punti focali sono equidistanti dal punto principale O
1
(n12
f
S
1
1
1)
R R
2
1
F’
O
F
S’
l’equazione del “costruttore” diventa:
1
1
1
s
s'
f
Ingrandimento:
1
potenza
diottrica
f
s
y'
s'
m
y
s
s’
LENTI SOTTILI CONVERGENTI (positive)
I)
S
oggetto reale,
immagine reale
F’
y
y’
F
S’
F’
y
F
pellicola
schermo
y
obiettivo di
macchina fotografica
| m| << 1
F
F’
obiettivo di
proiettore
| m| >> 1
LENTI SOTTILI CONVERGENTI (positive)
II)
y’
y
oggetto reale,
immagine virtuale
F’
F
lente di ingrandimento,
oculari microscopio, telescopio
III)
y
F
y’ F’
oggetto virtuale,
immagine reale
LENTI SOTTILI DIVERGENTI (negative)
I)
y
F’
F
oggetto reale,
immagine virtuale
F
oggetto virtuale,
immagine reale
y’
II)
F’
y y’
III)
F
y’ F’
y
oggetto virtuale,
immagine virtuale
oculare cannocchiale
Sistemi ottici
Lo scopo principale di un sistema ottico risiede nel fornire l'immagine
corretta di un oggetto che, nel caso più semplice, è una figura piana
disposta perpendicolarmente all'asse ottico del sistema. Le condizioni
ideali per i sistemi centrati sono tre:
1. la luce entra nel sistema sotto forma di fasci parassiali;
2. i fasci formano angoli piccoli con l'asse principale del sistema;
3. l'indice di rifrazione è costante per tutti i raggi: il mezzo non è
dispersivo o la luce è sufficientemente monocromatica,
Solitamente si ha a che fare con con una luce non monocromatica: si deve
tener conto della dipendanza dell'indice di rifrazione dalla lunghezza
d'onda (dispersione).
Strumenti ottici
Gli strumenti ottici sono sistemi ottici progettati allo scopo
di aumentare il potere risolutivo dell'occhio.
LENTE
D'INGRANDIMENTO
Si tratta di una lente convergente, dotata di distanza focale molto
piccola, capace di formare un'immagine virtuale, dritta e ingrandita,
di un oggetto disposto fra la lente ed il fuoco della lente stessa.
CANNOCCHIALE
Strumento impiegato prevalentemente in astronomia formato da 2
lenti. Dato che l'oggetto è molto distante l'immagine fornita dalla
prima lente (obiettivo) si forma vicino al fuoco, molto piccola e
capovolta, mentre la seconda (oculare) fornisce una seconda
immagine virtuale ingrandita.
MICROSCOPIO
è formato essenzialmente da 2 lenti convergenti disposte a distanze
opportune. Posto un oggetto a in prossimità del fuoco si forma
un'immagine reale, capovolta e ingrandita, della quale si osserva
l'immagine virtuale, e ulteriormente ingrandita, mediante un oculare.
Microscopio semplice o lente di ingrandimento
y’
’
y
F
d’
si confronti con la situazione di visione distinta naturale:
y
0
d0
definiamo ingrandimento angolare:
y ' d 0
'
M
0
y d '
tan
Microscopio composto
oculare
s’
s
y
O
F1’
F2
y’=y0
F1
y0’
’
F2’
obiettivo
d’
y0 ' d 0 y '
' y'
M
- mob Moc
0 ' y
y0 d ' y
tipic. mob 50 200, Moc 5 10
M 200 2000
Telescopio a rifrazione
telescopio galileiano (cannocchiale)
oculare
F1’ F2
’
obiettivo
'
f1
M
0
f2
MGalileo = 33
Telescopio a rifrazione
telescopio astronomico (kepleriano)
oculare
F1’
obiettivo
'
f1
M
0
f2
F2
Telescopio a riflessione
telescopio newtoniano
F1
specchio
piano
non c’è
aberrazione cromatica
obiettivo
(specchio concavo)
oculare
'
f1
M
0
f2
MNewton 40
Aberrazioni cromatiche
aberrazione cromatica : f dipende dalla lunghezza d’onda della luce
perché da questa dipende n del materiale, se l’immagine è a fuoco per
uno dei colori componenti della luce bianca sarà leggermente fuori
fuoco per gli altri componenti
F
F’
Aberrazioni monocromatiche
aberrazioni monocromatiche : i raggi paralleli all’asse hanno in
realtà un’immagine che varia in funzione delle loro distanza dall’asse
Sistemi complessi di lenti vengono progettati in modo che le singole
aberrazioni di ciascun elemento tendano a compensarsi.












