EQUILIBRIO STATICO
1
FORZE DI REAZIONE VINCOLARE
Sono forze di contatto esercitate dai vincoli cui è
soggetto il corpo. L’azione del vincolo è rappresentata da
una forza detta reazione vincolare.
P
Il corpo è in equilibrio
sotto l’azione della
forza peso P e della
reazione vincolare N
(forza normale alla
superficie di contatto).
2
DAI PUNTI MATERIALI AI CORPI
ESTESI
Un corpo rigido è un insieme di particelle le cui distanze
reciproche rimangono immutate nel tempo qualsiasi
siano le forze e i vincoli a cui è soggetto.
Un corpo rigido è un sistema materiale indeformabile (se
le forze sono sufficientemente piccole)
Esempio: corpo rigido e forza di gravità.
Lo pensiamo decomposto in tante particelle di massa m1,
m2, m3…che risentono della accelerazione g
3
Dai punti materiali ai corpi estesi
I solidi
I fluidi
I gas
Centro di massa
L’esperienza mostra che un sistema di forze parallele
applicate ad un corpo rigido è riconducibile ad un’unica
forza risultante con la direzione identica alle forze
applicate, l’intensità pari alla somma delle intensità
tenendo conto del verso, ed il verso é come quello delle
forze prevalenti. Il punto di applicazione della forza
risultante è il baricentro
P m1 g m2 g m3 g ... mg
g
P
5
Forze, equilibrio, movimento
F
mg
a
b
Deambulazione
STATICA
In questo caso, pur essendo
la somma delle forze esterne
pari a zero, la somma dei
momenti non è nulla e quindi
il corpo ruoterà.
Affinché un corpo rigido sia in quiete è necessario che:
1) La somma di tutte le forze esterne sia nulla
2) La somma di tutti i momenti delle forze sia nulla
8
Equilibrio di un corpo rigido
Un corpo rigido si trova in equilibrio quando non modifica il suo moto
traslatorio e rotatorio.
Condizione necessaria e sufficiente affinché questo avvenga è che sia nulla la
risultante di tutte le forze (equilibrio traslatorio) e nulla la risultante di tutti
i momenti delle forze (equilibrio rotatorio).
Fi 0
Mi 0
PRODOTTO VETTORIALE
È una grandezza vettoriale: il modulo è dato dal
prodotto dei moduli e del seno dell’angolo formato,
direzione e verso si ricavano dalla regola della mano
destra.
V
V a b ab sin
b
a
Il prodotto vettoriale NON
gode della proprietà
commutativa: b a a .b
10
ESEMPIO PRODOTTO VETTORIALE
Momento di una forza fatto rispetto ad un punto
materiale
M r F rF sin
M
r
F
11
MOMENTO DI UNA FORZA
Il momento di una forza è determinato dalla componente
della forza normale alla retta di azione a.
a
Polo
M aF
Fp
Fn
F
12
LEVE
La leva è un corpo rigido, di solito oblungo, libero di
ruotare intorno a un asse fisso; serve a equilibrare una
resistenza R con un’altra forza FP detta potenza.
13
LEVE
Applicazione delle proprietà delle leve nella vita pratica.
L’utilità è applicare una
FP < R
oppure applicare una FP lungo una direzione più
conveniente
Le rette di azione sono complanari fra loro e in un piano
perpendicolare all’asse di rotazione
Il punto di intersezione è detto fulcro della leva.
14
LEVE
Condizioni
necessarie
affinché una leva sia in
quiete :
Leva
i ) FP R N 0
N
ii ) FP a R b
cioè il risultante dei
momenti
delle
forze
rispetto al punto di
intersezione
dell’asse
con il piano delle forze
è nullo.
a
FP
b
F
R
15
LEVE
a
b
1° genere
FP
R
F
FP
F
2° genere
R
FP
3° genere
R
F
F: fulcro, FP: potenza, R: resistenza, a, b: bracci
16
LEVE
FP
Pinze: leva di primo genere
R
fulcro
R
FP
Schiaccianoci: leva di secondo genere
FP
Molle: leva di terzo genere
FP
17
LEVE
Guadagno meccanico della leva: G=R/FP
FP•a = R•b G = a/b
La leva si dice vantaggiosa, svantaggiosa o
indifferente a seconda che il guadagno G sia maggiore,
minore o uguale ad uno, rispettivamente.
1° genere: G può assumere qualunque valore
2° genere: b < a G > 1
3° genere: b > a G < 1
18
Strutture anatomiche ed equilibrio dei corpi
I muscoli: generano le forze.
I tendini :applicano le forze alle
strutture ossee.
Le ossa: modificano la direzione
delle forze per avere risultante
nulla delle forze e dei momenti
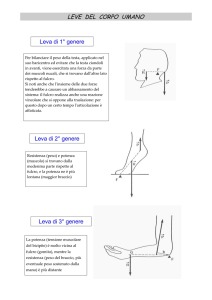
LEVE DEL CORPO UMANO
R
F
FP
Leva di 1o genere
F
R
FP
Leva di 2o genere
R
FP F
Leva di 3o genere
20