trasparenze ppt

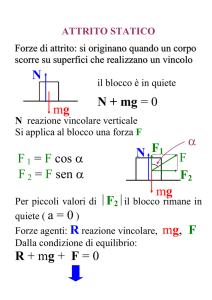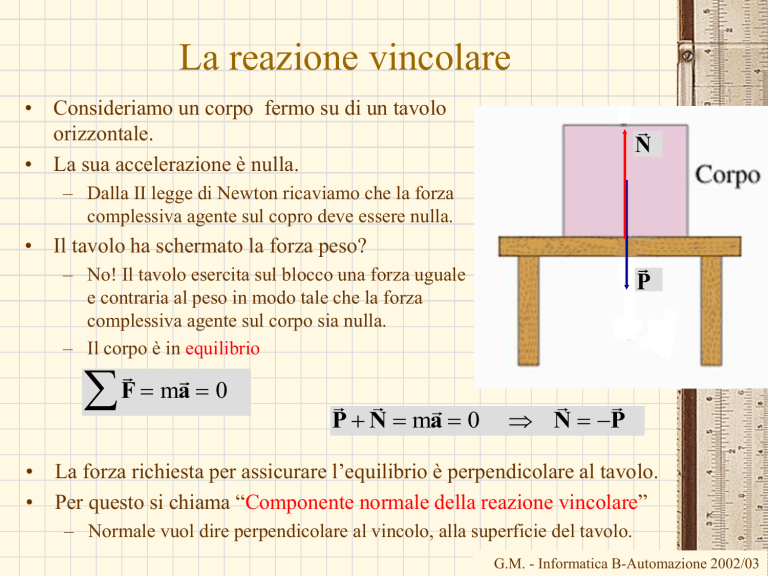
La reazione vincolare
• Consideriamo un corpo fermo su di un tavolo
orizzontale.
• La sua accelerazione è nulla.
N
– Dalla II legge di Newton ricaviamo che la forza
complessiva agente sul copro deve essere nulla.
• Il tavolo ha schermato la forza peso?
– No! Il tavolo esercita sul blocco una forza uguale
e contraria al peso in modo tale che la forza
complessiva agente sul corpo sia nulla.
– Il corpo è in equilibrio
 F  ma  0
P  N  ma  0
P
 N  P
• La forza richiesta per assicurare l’equilibrio è perpendicolare al tavolo.
• Per questo si chiama “Componente normale della reazione vincolare”
– Normale vuol dire perpendicolare al vincolo, alla superficie del tavolo.
G.M. - Informatica B-Automazione 2002/03
La reazione vincolare
• Le reazioni vincolari si manifestano ogni volta
che esiste un vincolo, ossia un impedimento, al
moto di un corpo.
– Nel caso in considerazione, il piano orizzontale
impedisce al corpo di occupare una qualsiasi
posizione al di sotto del piano stesso: il corpo non
può penetrare nel piano orizzontale.
• La reazione vincolare:
– Ha sicuramente una componente normale al
vincolo diretta verso la parte di spazio consentito
(componente Normale N)
• Se non ce l’ha vuol dire che non c’è contatto del
corpo con il vincolo
– può avere una componente parallela al vincolo
• se ce l’ha si chiama “Forza di attrito”
– Statico: il corpo è fermo rispetto al vincolo
– Dinamico: il corpo striscia sul vincolo.
• La reazione vincolare agisce per contatto
N
P
 F  ma  0
N.B.: La reazione vincolare
non ha una espressione che
permette di determinarla: essa
va determinata caso per caso
utilizzando le leggi di
Newton.
G.M. - Informatica B-Automazione 2002/03
La forza di attrito statico
• La Forza di attrito è la componente parallela al vincolo della Reazione
Vincolare.
• Si parla di attrito statico se non c’è scorrimento tra il corpo e la
superficie su cui il corpo è poggiato
N
P
• Nel caso di un corpo appoggiato su un piano orizzontale abbiamo visto
che la sola componente normale è sufficiente a garantire l’equilibrio del
corpo.
• La forza di attrito, ossia la componente parallelo al vincolo è nulla.
G.M. - Informatica B-Automazione 2002/03
La forza di attrito statico
• Applichiamo al corpo una forza orizzontale. Si osserva che:
– Per piccoli valori della forza applicata il corpo resta ferma.
– Se si aumenta la forza applicata, superato un certo valore il corpo si mette
in movimento.
• Consideriamo per ora il caso in cui il corpo resta ancora fermo.
y
R v x  fo  0
Rv
modulo
componenti
fo
P
x
Px  R v x  fo x  0
P  R v  fo  ma  0
 Py  R v y  fo y  0
Pz  R v z  fo z  0
componenti
 mg  R v y  0
Rvz  0
R v x  fo
R v y  mg
Rvz  0
Rvx=forza di attrito statico
G.M. - Informatica B-Automazione 2002/03
Il valore massimo
della forza di attrito statico
• Non esiste una espressione per determinare la forza di attrito statico
(intensità, direzione, verso)
– La forza di attrito statico si determina applicando le leggi di Newton.
– Nel caso precedentemente analizzato abbiamo trovato:
• L’intensità uguale a quella della forza orizzontale applicata
• direzione quella della forza orizzontale applicata
• verso opposto.
• Abbiamo anche osservato che aumentando l’intensità della forza
orizzontale applicata, raggiunto un certo valore, il corpo si mette in
moto.
– Il modulo della forza di attrito statico è limitato superiormente, non può
aumentare oltre un certo valore!
– Il valore massimo della forza di attrito statico dipende
Fas  ms N
• dal modulo della componente normale N della reazione vincolare.
• dalla natura e dallo stato delle superfici a contatto (ms)
• dalla temperatura
– Non dipende
• Dalla superficie di appoggio
G.M. - Informatica B-Automazione 2002/03
La forza di attrito statico
• Il contatto avviene in un numero finito
di asperità.
• Si verificano delle deformazioni, quindi
forze elastiche.
• L’area di effettivo contatto è
–
proporzionale alla deformazione
complessiva
– proporzionale alla forza complessiva
esplicata (N).
• L’area di effettivo contatto è la stessa
nei due casi (N è lo stesso nei due casi).
Pochi punti molto deformati
Molti punti
poco deformati
G.M. - Informatica
B-Automazione 2002/03
La forza di attrito dinamico
• Se le superfici a contatto sono scabre e c’è scorrimento tra esse.
• Nel caso dell’attrito dinamico è possibile determinare tutto: modulo
direzione e verso.
– È diretta in verso apposto al moto (stessa direzione della velocità ma verso
opposto)
Superfici lisce: i
– Il modulo della forza è dato da: Fad  m d N
• La forza di attrito dinamico
– dipende
• dalla natura e dallo stato delle superfici a contatto (md)
• dalla componente normale (N)
• dalla temperatura
– non dipende
coefficienti di attrito
statico e dinamico
sono nulli!
La reazione vincolare
ha solo la
componente normale
• dalla superficie di appoggio
• dalla velocità di scorrimento delle superfici a contatto
• La forza di attrito dinamico è più piccola del valore massimo della forza
di attrito statico (md< ms)
– Nel caso dell’attrito statico si formano delle vere e proprie saldature nei
punti di effettivo contatto, che non hanno il tempo di formarsi nel caso
dinamico.
G.M. - Informatica B-Automazione 2002/03
I coefficienti di attrito
ms
md
Legno su legno
0.25-0.5
0.2
Vetro su vetro
0.9-1.0
0.4
0.6
0.6
0.09
0.05
1.0
0.8
0.04
0.04
0.04
0.04
Superfici
Acciaio su acciaio, superfici
pulite
Acciaio su acciaio, superfici
lubrificate
Gomma su cemento armato
asciutto
Sci di legno cerato su neve
secca
Teflon su teflon
Questi numeri sono indicativi, i coefficienti di attrito dipendono molto
dallo stato delle superfici, dalla temperatura, dall’umidità, etc.
G.M. - Informatica B-Automazione 2002/03
Tensione nelle corde
• La corda è un dispositivo per trasmettere (applicare) una forza ad un
corpo.
– Le corde possono trasmettere forze aventi la stessa direzione della corda
– Inoltre possono solo tirare
• Consideriamo un corpo di massa m attaccato ad una corda.
– Tiriamo la corda con la forza F2.
– Chiamiamo F1 la forza che il corpo di massa m esercita sulla corda
– Per la terza legge di Newton, la forza che la corda esercita sul corpo sarà
Fc=-F1.
m
F1
F2
Applichiamo la seconda
legge di Newton alla corda:
F2
In condizioni statiche
F1  F2  ma
a  0  F1   F2  Fc  F2
m
Fc=-F1
Corda ideale: m=0, L=costante
In condizioni dinamiche si arriva allo stesso
risultato se la massa della corda è nulla
m  0G.M.
F1  B-Automazione
F2  Fc2002/03
 F2
- Informatica
Tensione nelle corde
• Nelle corde ideali la forza si
trasmette identica lungo tutta la
corda.
– Tensione della corda
– Se si taglia la corda in un punto
qualsiasi la parte a destra del
taglio eserciterà su quella a
sinistra una forza di modulo pari
alla tensione e viceversa.
– La tensione può essere messa in
evidenza inserendo una molla nel
taglio e osservando il suo
allungamento
– A volte si usano delle carrucole
ideali (piccolo raggio e piccola
massa, senza attriti) per cambiare
la direzione della tensione.
• Le carrucole ideali non
cambiano l’intensità della
tensione.
Fsd
Fds  T  ma
T
Fds
m  0G.M.
Fds B-Automazione
T  Fsd
T
- Informatica
2002/03
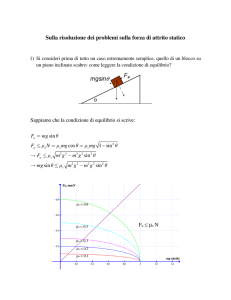
Un blocco di 28.0 kg è collegato ad un secchio vuoto di 1 kg mediante una
corda che scorre su una carrucola ideale priva di attrito. Il coefficiente di
attrito statico tra il tavolo e il blocco è 0.450 mentre quello di attrito
dinamico è 0.320. Il secchio viene gradualmente riempito di sabbia fino a
che il sistema inizia a muoversi.
• calcolare la massa della sabbia versata nel secchio
• l'accelerazione del sistema
• la tensione nella corda un istante prima che inizi il moto e durante il
moto.
Applica
zione
• Indichiamo con m1 la massa del blocco,
con m2 quella del secchio (msc) e della
sabbia (msb)
• Troviamo le forze agenti su ciascuno dei
corpi.
• Blocco
– La forza peso
– La tensione della fune
– La reazione vincolare del tavolo
composta da
• La componente normale
• La forza di attrito
• Secchio
– La forza peso
– La tensione della fune
G.M. - Informatica B-Automazione 2002/03
Disegnamo le forze.
y
Costruiamo il diagramma del corpo libero
N
T1
Fas
T2
x
Fas
P1
P1
blocco
P2
• Fissiamo un sistema di riferimento
inerziale (Laboratorio)
• Scriviamo la seconda legge dei
Newton per i due corpi:
T2
P2
secchio
• Proiettiamo sugli assi
coordinati
blocco P1  Fas  N  T1  m1a1
secchio
N
T1
Applica
zione
x :  Fas  T  m1a1x
y : N  m 1g  m 1a 1y
P2  T2  m2 a2
P2  T2  0  T2  P2
In condizioni statiche l’accelerazione del
secchio è nulla, quindi la corda si dispone lungo
la verticale, la tensione ha solo la componente
verticale
G.M. - Informatica B-Automazione 2002/03
y
N
T1
Fas
T2
x
P1
secchio
Si ottiene:
T2
Applica
zione
P2
P1
P2
blocco
Fas
N
T1
blocco
secchio
In condizioni statiche
P1  Fas  N  T1  0
P2  T2  0
x :  Fas  T  0
y : N  m 1g  0
x:
y : T  m 2g  0
T  m2g Fas  T  m2g N m1g
Ma la forza di attrito statico è limitata superiormente:
Fas  ms N  m2 g  ms N ms m1g
Il sistema comincerà a muoversi quando
m2 g  m sm1g  m2  ms m1  0.450  28.0kg  12.6kg
G.M. - Informatica B-Automazione 2002/03
Poichè
m2  msc  msb
 msb  m2  msc  12.6kg 1.0kg 11.6kg
Applica
zione
Non appena il sistema inizia a muoversi cambiano le condizioni dinamiche:
y
N
T1
Fad
T2
x
Fad
P1
P1
blocco
P2
blocco P1  Fad  N  T1  m1a1
secchio P2  T2  m2 a2
Ricordiamo che
N
T1
Fad  m d N
Osserviamo che a1y  0
T2
P2
secchio
x :  Fad  T  m1a1x
y : N  m 1g  m 1a 1y
x:
y : T  m 2g  m 2 a 2y
Il blocco rimane a contatto con il tavolo durante il
suo moto y1(t)=0
G.M. - Informatica B-Automazione 2002/03
y
N
T1
Fad
T2
x
Fad
P1
T2
x :  md N  T  m1a 1x
y : N  m1g  0
Applica
zione
P2
P1
P2
blocco
N
T1
blocco
secchio
x:
secchio y :
T  m 2g  m 2 a 2y
Abbiamo tre equazioni e 4 incognite: T, N, a1x, a2y. Troppe!!
Sfruttiamo il fatto che la corda è ideale, la sua lunghezza resta costante
per qualunque valore delle tensione.
Se il blocco avanza di un tratto x1 (positivo), il secchio si abbassa di
y2 (negativo)
x1  y2

x1
y2

t
t
v x1  v y2
 a x1  a y 2
G.M. - Informatica B-Automazione 2002/03
y
N
T1
Fad
T2
x
P1
P1
blocco
P2
Da cui
T  m 2g  m 2a 2 y
Ricavando T dall’ultima e
sostituendo nella seconda:
a1x
T2
Applica
zione
P2
secchio
N  m1g
m d N  T  m1a1x
N  m1g  0
Fad
N
T1
m d m1g  T  m1a1x
T  m 2g  m 2a 1x
T  m2g  m2a 1x
m d m1g  m2g  m2a 1x  m1a 1x
m 2 g  m d m1g

m1  m 2
2
2
m 2 g  m d m1g m1m 2g  m 2 g  m 2 g  m d m1m 2g
T  m 2g  m 2

m1  m 2
m1 G.M.
m 2- Informatica B-Automazione 2002/03
y
N
T1
Fad
T2
x
Fad
P1
P1
blocco
P2
a1x
m 2 g  m d m1g

m1  m 2
m11  m d 
m1  m2
T2
Applica
zione
P2
secchio
L’accelerazione è costante: il moto dei due
corpi è uniformemente accelerato
m1m 2g1  m d 
T
m1  m2
T  m 2g
N
T1
 m2 g
Confrontiamo la tensione T con il caso
statico T=m2g
m 11  ms 
m1  m 2
m2
m1  m1ms
 m2 g
 m2 g
m1  m 2
La tensione nel caso dinamico è più piccola che in quello statico
G.M. - Informatica B-Automazione 2002/03
Le resistenze passive
• Con questo nome si indica la forza che un fluido esercita su di un corpo
che si muove al suo interno (un'automobile che si muove nell'aria, un
sasso che cade nell’acqua, una goccia di pioggia che cade nell’aria).
• La resistenza passiva è sempre opposta al moto.
• Se la velocità del corpo è piccola allora la forza è proporzionale
all’opposto della velocità:
R p  bv
Per una sfera di raggio r, b=6prh, in h cui è la
viscosità del mezzo:
Glicerina
1.5 Ns/m2 (poise)
Olio lubrificante 20°
0.03
Acqua 20°
1.0x10-3
Aria 20°
1.8x10-5
• Se la velocità del corpo è elevata allora l’intensità della
resistenza passiva diventa proporzionale al quadrato della
velocità:
C  coefficiente aereodinamico 0.4  1
1
2
D  CAv dove   densità del fluido
2
G.M. - Informatica B-Automazione 2002/03
A = area efficace
Le resistenze passive
• Consideriamo un moto di caduta che avviene in presenza di una
resistenza passiva.
• Inizialmente la velocità è nulla, la resistenza passiva è nulla,
l’accelerazione è quella di gravità, caso (a).
• Man mano che aumenta la velocità, la resistenza passiva aumenterà,
l’accelerazione sarà minore di g, ma la velocità continuerà ad aumentare,
caso (b).
• La velocità continuerà ad aumentare fin
tanto che la resistenza passiva diventa
uguale al peso, caso (c).
– Da questo punto in poi il moto sarà
uniforme
– La velocità del moto uniforme
viene chiamata velocità limite.
– per distanza di regime si intende la
distanza che il corpo deve
percorrere per raggiungere il 95%
della velocità limite.
G.M. - Informatica B-Automazione 2002/03
Resistenza passiva-alcuni esempi di
velocità limite e di distanza di regime
G.M. - Informatica B-Automazione 2002/03
Moto di caduta di un chicco di grandine
• Trascuriamo la spinta di Archimede, data la grande differenza
P  R p  ma
di densità tra il ghiaccio e l’aria (circa un fattore 1000)
ma  P  bv
• Le forze agenti sono: la forza peso e al resistenza passiva
ma x  bv x
• La velocità iniziale sia nulla.
ma y  bv y  mg
• Consideriamo un sistema di riferimento con l’asse y verticale.
ma z   bvz
• Per quanto riguarda gli assi x e z, le soluzione vx=0 e
dv y
b
mg 
vz=0 soddisfano l’equazione differenziale e le condizioni

vy 

dt
m
b 
iniziali.
– Il moto avviene lungo
mg
l’asse y
ponendo v'  vy 
si ha
dv'  dv y
b
risostituendo
vy 
mg 
mg 
 vyo 
e


b
b

b
t
m
b
dv'
b
 t
  v' La cui soluzione è:
v'  v' o e m
dt
m
b

 t
mg
vy  
1  e m 
b 

Per t che tende all’infinito la velocità tende alla velocità limite mg/b
G.M. - Informatica B-Automazione 2002/03