Espressioni logiche e algebra di Boole. Analisi di schemi logici
annuncio pubblicitario
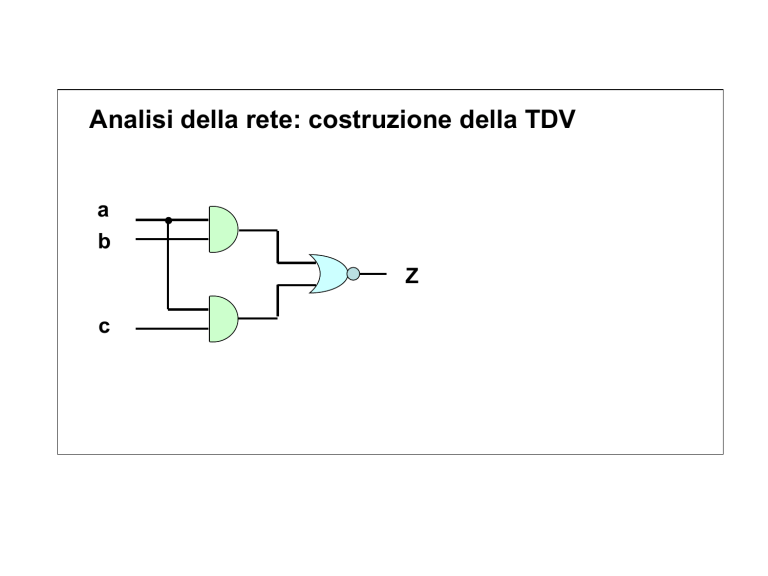
Analisi della rete: costruzione della TDV a b Z c Costruzione della tabella della verità F1 a b F1= ab F3 F2= ac Z c F3 = F1+ F2 Z = /F3 F2 Z = ab + ac Costruzione della tabella della verità Z = ab + ac F1= ab F2= ac F3 = F1+ F2 Z = /F3 a 0 0 0 0 1 1 1 1 b c 0 0 1 1 0 0 1 1 0 1 1 0 0 1 1 0 F1 F2 F3 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1 1 Z 1 1 1 1 1 0 0 0 Costruzione di reti logiche equivalenti Primo passo: l’espressione logica a b Z c Z = ab + ac Manipolazione di Espressioni logiche con i teoremi dell’algebra di Boole Z = ab + ac = …??? Manipolazione di Espressioni logiche con i teoremi dell’algebra di Boole Z1 = a (b + c) Z = ab + ac = Z2 = a + b + c Z3 = a + b c Z4 = ab ac Espressioni logiche equivalenti Z1 = a (b + c) Z2 = a + b + c Z3 = a + b c Z4 = ab ac Verificare l’equivalenza di queste espressioni Prima soluzione: costruzione della TDV Z1 = a (b + c) TDV Z2 = a + b + c TDV Z3 = a + b c TDV Z4 = ab TDV ac Seconda soluzione: impiego di un simulatore logico Z1 = a (b + c) Schematico Z2 = a + b + c Schematico Z3 = a + b c Schematico Z4 = ab Schematico ac TDV Analisi TDV uno tramite strumento TDVdi simulazione TDV Verificare l’equivalenza delle reti (Mappa di karnaugh) Z1 Z2 Z 3 Z4 00 01 11 10 00 01 11 ? 10 (…si poteva usare anche la tabella della verità…) Verificare l’equivalenza delle reti (Mappa di karnaugh) Z1 Z2 Z 3 Z4 00 00 01 11 1 01 11 10 1 10 Espressione logica Z1 Z2 Z 3 Z4 00 00 01 11 10 1 01 11 10 1 Zc = Z1 Z2 Z3 Z4 + Z1 Z2 Z3 Z4 Schema logico Z1 Z2 Z3 Z4 Zc Z1 Z2 Z3 Z4 Schema logico Z1 Z2 Z3 Z4 Una rete equivalente? Zc Z1 Z2 Z3 Z4 Schema logico Z1 Z2 Z3 Z4 Zc Z1 Z2 Z3 Z4 Manipolazione di Espressioni logiche con i teoremi dell’algebra di Boole Z1 = a (b + c) Z = ab + ac = Z2 = a + b + c ? Z3 = a + b c Z4 = ab ac
