Qualche cenno
su circuiti con resistenze
per esercitazioni in laboratorio
Andrea Ventura
Scuola Estiva di Fisica 2015
Dipartimento di Matematica e Fisica “E. De Giorgi”
Università del Salento
Grandezze e unità di misura
• Le grandezze fondamentali dell’elettricità sono:
– la carica elettrica, la corrente elettrica e il potenziale elettrico.
•
La corrente (I) è definita come la quantità di carica elettrica (q)
che fluisce in un punto di un circuito nell’unità di tempo:
dq q
I
dt t
•
per t (e dunque q) sufficientemente piccoli
La corrente elettrica si misura in Ampere (A) pari a coulomb al
secondo.
• Il potenziale elettrico (V) è l’energia potenziale, dovuta al campo
elettrico, per unità di carica.
• Viene misurato in Volt (V) pari a Joule diviso per Coulomb.
• La differenza di potenziale (d.d.p.) tra due punti è detta anche
tensione tra due punti.
Legge di Ohm
• La corrente elettrica (I) che scorre in un conduttore è direttamente
proporzionale alla differenza di potenziale elettrico (V) applicata alle sue
estremità A e B:
I
VA VB
R
• Questa relazione è detta anche legge di Ohm.
• La grandezza R, che è il rapporto fra la corrente e la tensione, è chiamata
resistenza del conduttore.
• L’inverso della resistenza è chiamato conduttanza (G):
G
1
R
• In un grafico corrente/tensione
la legge di Ohm è rappresentata
da una retta passante per l’origine
ed avente pendenza 1/R
Tensione VA – VB
Resistenza e seconda legge di Ohm
• La resistenza o resistore è un elemento circuitale costituito da un materiale che
può essere attraversato da cariche elettriche.
• Il suo valore R dipende dal materiale e dalle dimensioni.
•La resistenza è legata alla resistività del materiale (ρ) dalla relazione:
R
l
A
dove A rappresenta la sezione trasversa e l la lunghezza del conduttore.
• La resistenza si misura in Ohm (Ω).
• In fisiologia si usa frequentemente il concetto di conduttanza (G) che è l’inverso
della resistenza.
• L’unità di misura della conduttanza è il Siemens (S).
•Resistività di vari materiali:
•Conduttori:
Rame, ferro, alluminio
•Semiconduttori:
Germanio, silicio, boro
•Isolanti:
Vetro, plastica, polistirolo
= 10- 8 m
= da 10- 3 a 10 2 m
= 10+15 m
Vari tipi di resistori
Collegamento di resistenze
Resistenze in serie
Resistenze in parallelo
Collegamento di resistenze in serie
R1
A
Req
R2
C
B
I
+
C
A
I
-
+
-
VA R1I R2 I VC
VA Req I VC
VA VC ( R1 R2 ) I
VA VC Req I
Req R1 R2
Collegamento di resistenze in parallelo
I1 R1
Req
R2
A
B
B
A
I2
I
+
V A VB
I
1
R1
I V A VB
2
R2
-
+
I
I
VA VB VA VB VA VB
Req
R1
R2
1
1
1
Req R1 R2
-
VA VB
Req
Esercitazione in laboratorio
• In laboratorio dapprima useremo lampadine al posto dei resistori.
• Esse, collocate all’interno di circuiti, oppongono resistenza. La corrente elettrica,
attraversando il filo conduttore all’interno del bulbo di vetro, lo riscalda per effetto
Joule fino a produrre luce.
• In base all’effetto Joule, la potenza elettrica P che viene trasformata in calore da
un qualsiasi elemento circuitale attraversato da una corrente elettrica I ai cui capi
è presente una tensione V, è data da:
P IV
• Per resistori di tipo ohmico (cioè tali che V=RI), la suddetta relazione diventa:
P I R V / R
2
2
Esercitazione in laboratorio con lampadine
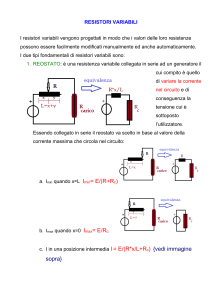
Se tutte le lampadine in figura sono identiche, quale circuito genera più luce?
P=I•V=R•I2
I=V/R
–
+
1.5 V
–
+
1.5 V
Rt=(R1·R2)/(R1+R2)=0.5
I=3 A
P=4.5 Watt
Rt= R1+R2 = 2
I=0.75 A
P=1.125 Watt
Esercitazione in laboratorio con resistori
Successivamente passeremo a impiegare resistori in serie o in parallelo per
realizzare i nostri circuiti e saremo più quantitativi. Inoltre, in luogo di batterie
(aventi resistenze interne non trascurabili che altererebbero le nostre misure)
abbiamo generatori di tensione stabilizzati, con valori di tensione impostabili.
Esempio n.1
Qual è il valore della resistenza equivalente ai due resistori in serie?
3k
50 V
2 k
Esempio n.2
Calcolare la corrente nel seguente circuito. Qual è la resistenza equivalente dei
due resistori in parallelo? Calcolare la tensione ai capi di ciascun resistore e le
correnti nei vari rami.
110 V
11k
11k
Strumentazione elettronica di base
VOLTMETRO può essere analogico o
digitale: misura le differenze di
potenziale continue ed alternate. Va
posto in parallelo al generatore.
AMPEROMETRO analogico e
digitale: misura le correnti continue
ed alternate. In serie al generatore.
OHMMETRO analogico e digitale:
misura le resistenze.
MULTIMETRO analogico e digitale:
raggruppa i tre strumenti sopracitati in
uno solo.
Materiale per l’esercitazione in laboratorio
Generatore
di tensione
Voltmetro
analogico
Vaschetta con cavetti di
collegamento e connettori vari
Resistenze
Multimetro
digitale
(o tester)
Lampadine
Piastra millefori
per realizzare
circuiti
(o breadboard)
Guida per l’esercitazione in laboratorio - Circuiti
In laboratorio vi sono sei tavoli con la strumentazione predisposta. Una volta
costituiti i gruppi, indicare i propri nominativi (e l’Istituto di provenienza):
______________________
______________________
______________________
______________________
( ___________________
( ___________________
( ___________________
( ___________________
di __________ )
di __________ )
di __________ )
di __________ )
1) Costruire un circuito a maglia unica attraverso breadboard e cavetti in cui il
generatore (a una fissata tensione V, misurata tramite il voltmetro posto in parallelo
al generatore) è posto in serie con una lampadina, e misurare la corrente I (usando
il multimetro in modalità amperometro). Stimare R della lampadina noto che V=RI.
2) Ripetere la misura usando prima due e poi tre lampadine in serie. I varia lungo il
circuito? Quanto vale la tensione V ai capi di ogni lampadina?
3) Ripetere la misura ponendo due e poi tre lampadine in parallelo. Ij varia su ciascun
ramo j? E quanto vale V tra i due nodi ai capi del parallelo delle lampadine?
4) Quanto si illuminano le lampadine nelle suddette configurazioni? Confrontare
qualitativamente e commentare in termini di potenza dissipata.
5) Ripetere i suddetti punti 1)-3) ma impiegando al posto delle lampadine delle
resistenze, per le quali si sarà preventivamente misurata Ri tramite il multimetro.
Leggi di Kirchoff
Prima legge o legge della
corrente: la somma di tutte le
correnti entranti in un qualsiasi
punto di un circuito elettrico deve
essere uguale a zero (non vi può
essere accumulo di carica).
Seconda legge o legge della
tensione: la somma di tutti i
potenziali elettrici lungo un circuito
chiuso deve essere uguale a zero.
ANALISI CIRCUITALE: LEGGE DI
KIRCHOFF PER LA CORRENTE
Indipendentemente dai componenti collegati,
la somma di tutte le correnti che entrano ed
escono da un nodo è pari a zero.
1. Corrente entrante nel nodo : +ve
2. Corrente che lascia il nodo : -ve
Quindi in A,
Quindi in B,
I 0 i i i i i i
I 0 i i i i i i 0
1
2
4
5
3
6
4
4
5
2
6
3
i1 i4
ANALISI CIRCUITALE: LEGGE DI
KIRCHOFF PER LA TENSIONE
+
Quindi nel circuito,
-
+
In un circuito chiuso, la somma di tutte le
cadute di potenziale è zero.
1. La corrente viaggia dal potenziale più
alto al più basso.
2. Una corrente positiva fluisce dal + al –
all’interno di un generatore di tensione
continua (batteria).
V1
dovuto alla (2)
i1 R1
dovuto alla (1)
V2
dovuto alla (2)
i1 R2
dovuto alla (1)
0
V1 V2
i1
R1 R2
Utilizzo delle regole di Kirchoff
• Disegna il circuito segnando ogni cosa nota o incognita
• Per ciascuna serie di componenti, assegna una direzione
alla corrente I
• non preoccuparti se scegli la direzione sbagliata, il
risultato sarà corretto ma di segno opposto
• Scrivi un’equazione per la conservazione della carica in
ciascun vertice (nodo)
• Scrivi un’equazione per ciascun loop (maglia)
• In una sorgente di f.e.m. (forza elettromotrice, come una
batteria), andando da – a + dà un V positivo, da + a – è un V
negativo
• Risolvi tutte le equazioni e ricaverai le incognite
Esercizio n.3
Usare la legge della corrente di Kirchoff e la legge per la tensione per
calcolare la corrente attraverso ciascuno dei resistori e la tensione ai loro capi
4k
3k
i1
i2
9V
+
i3
6k
2k
+
3V
i1 i 2 i3
R1i1 R3i 3 0
V*
1
V*2 R3i3 ( R2 R4 )i 2 0
i1 i 2 i3
V1 R1i1 R3i3 0
V2 R3i 3 ( R2 R4 )i 2 0
1° legge di Kirchoff
(dei nodi)
2° legge di Kirchoff
(delle maglie)
i 3 5 / 8K 0.625 mA
i 2 9 / 8K 1.125 mA
i 7 / 4K 1.75 mA
1
Una corrente positiva fluisce dal + al – all’interno di
un generatore di tensione continua (batteria).
*