legge della circuitazione

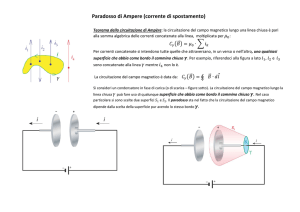
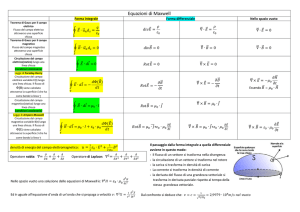
LEGGE DELLA CIRCUITAZIONE
Un campo di forze si dice
CONSERVATIVO
se il lavoro fatto dal campo è indipendente
dal percorso ma dipende solo dal punto
iniziale e dal punto finale
LEGGE DELLA CIRCUITAZIONE
Il fatto che il campo elettrico sia
conservativo è fondamentale per la
definizione di potenziale elettrico
LEGGE DELLA CIRCUITAZIONE
A
LAB
VA  VB 
Q
B
Infatti la differenza di
potenziale tra due
punti è definita come
il lavoro fatto dal
campo quando la
carica unitaria è
spostata da un punto
all’altro
LEGGE DELLA CIRCUITAZIONE
A
LAB
VA  VB 
Q
B
Se il lavoro
dipendesse anche dal
percorso dovremmo
pure specificare il
percorso e quindi non
avremmo una buona
definizione
LEGGE DELLA CIRCUITAZIONE
L=0
TEOREMA: In un
campo conservativo il
lavoro fatto su un
percorso chiuso è
uguale a zero,
qualsiasi sia il
percorso
LEGGE DELLA CIRCUITAZIONE
A
2
1
B
Infatti, ogni
percorso chiuso
può essere diviso
in due parti, 1 e 2,
aventi entrambe
come estremi due
punti A e B
LEGGE DELLA CIRCUITAZIONE
A
2
1
Il lavoro totale è
la somma di
quello
compiuto nei due
tratti
LL L
1
AB
B
2
BA
LEGGE DELLA CIRCUITAZIONE
A
2
1
B
Ma invertendo il
verso di percorrenza
il lavoro cambia
segno (infatti se
prima forza e
spostamento erano
concordi ora sono
discordi o viceversa)
LEGGE DELLA CIRCUITAZIONE
A
2
1
B
Quindi possiamo
dire che il lavoro
fatto da B ad A su
percorso 2 è uguale
a meno il lavoro da
A a B sullo stesso
percorso
2
2
BA
AB
L
 L
LEGGE DELLA CIRCUITAZIONE
A
2
Sostituendo nella
formula del lavoro:
LL L
1
AB
2
BA
L
1
B
2
BA
 L
2
AB
Si ottiene:
1
2
AB
AB
L L L
LEGGE DELLA CIRCUITAZIONE
A
2
1
Ma il campo è
conservativo per
ipotesi, quindi il
lavoro è
indipendente dal
percorso:
1
AB
L
B
L
2
AB
LEGGE DELLA CIRCUITAZIONE
Quindi, sostituendo:
A
2
L=0
1
AB
L
L
2
AB
L L L
1
AB
Otteniamo:
1
LL
1
AB
B
L
1
AB
Che era la tesi
2
AB
0
LEGGE DELLA CIRCUITAZIONE
Possiamo quindi dire che un campo di
forze conservativo è un campo in cui:
• Il lavoro è indipendente dal
percorso
• Il lavoro fatto su un percorso chiuso
è nullo
LEGGE DELLA CIRCUITAZIONE
Il lavoro è definito
dalla formula:
F
L  F  S  cos
α
S
Ma questa vale solo
se il percorso è
rettilineo e il campo
uniforme
LEGGE DELLA CIRCUITAZIONE
1
2
3
4
5
Nel caso generale
possiamo dividere il
percorso in tanti
piccoli pezzi quasi
rettilinei e calcolare
il lavoro su ciascuno
di questi pezzi
LEGGE DELLA CIRCUITAZIONE
1
Il lavoro sull’i-esimo
pezzettino sarà:
2
3
Li  Fi  Si  cos  i
4
Si
Fi
αi
LEGGE DELLA CIRCUITAZIONE
1
Il lavoro totale sarà
la somma di tutti
questi piccoli pezzi
2
3
n
4
Si
Fi
αi
L   Fi  S i  cos  i
i 1
LEGGE DELLA CIRCUITAZIONE
In realtà il calcolo è solo approssimato;
diventa esatto facendo tendere
all’infinito il numero dei pezzettini
n
L  Lim  Fi  Si  cos  i
n 
i 1
LEGGE DELLA CIRCUITAZIONE
In realtà il calcolo è solo approssimato;
diventa esatto facendo tendere
all’infinito il numero dei pezzettini
n
L  Lim  Fi  Si  cos  i
n 
i 1
LEGGE DELLA CIRCUITAZIONE
Invece del lavoro, con lo stesso
procedimento si può calcolare la differenza
di potenziale (che è lavoro per unità di
carica): basta prendere la forza per unità di
carica, cioè il campo elettrico
n
VA  VB  Lim  Ei  Si  cos  i
n 
i 1
LEGGE DELLA CIRCUITAZIONE
Questa operazione non è necessariamente
legata al campo elettrico; per ogni campo
vettoriale W noi possiamo calcolare in modo
matematico il limite
n
Lim  Wi  Si  cos  i
n 
i 1
LEGGE DELLA CIRCUITAZIONE
l
In particolare, se il
percorso è una linea
chiusa, il risultato
dell’operazione prende
il nome di
CIRCUITAZIONE del
vettore W
LEGGE DELLA CIRCUITAZIONE
In simboli:
l
n

C (W )  Lim  Wi  Si  cos  i
n 
i 1
LEGGE DELLA CIRCUITAZIONE
Nel caso del campo elettrico, però, la
circuitazione non è una pura operazione
matematica, ma indica il lavoro per unità di
carica sul percorso chiuso L
n

C ( E )  Lim  Ei  Si  cos  i
n 
i 1
LEGGE DELLA CIRCUITAZIONE
E siccome il campo elettrico è conservativo,
questo lavoro deve essere nullo.
Possiamo dunque esprimere in questo modo
la conservatività del campo elettrico

C ( E )  0
LEGGE DELLA CIRCUITAZIONE
Questa diventa, insieme col teorema di
Gauss, una delle leggi fondamentali
dell’elettrostatica.
A queste possiamo aggiungere la relazione
che lega campo elettrico a forza elettrica
LEGGE DELLA CIRCUITAZIONE

 sc ( E ) 
1
o
n
Q
k 1

C ( E )  0


F  qE
k