I
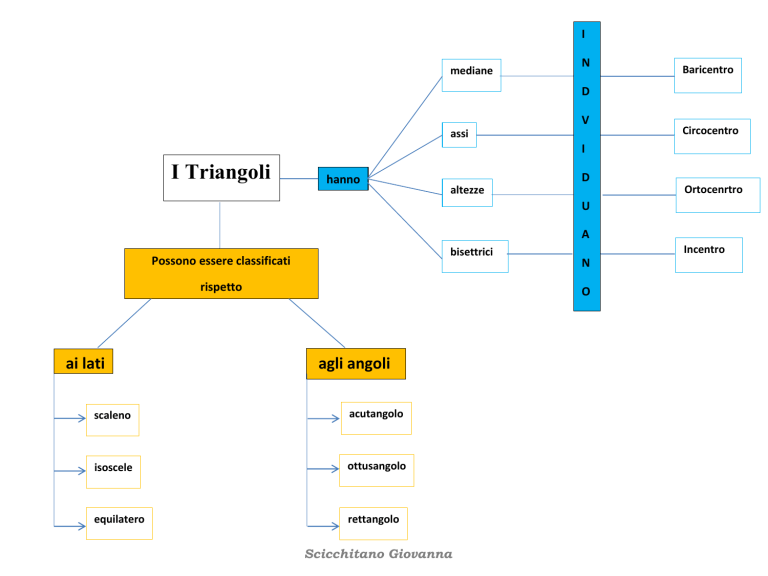
mediane
N
Baricentro
D
V
assi
Circocentro
I
I Triangoli
hanno
D
altezze
Ortocenrtro
U
A
bisettrici
Possono essere classificati
rispetto
ai lati
Incentro
N
O
agli angoli
scaleno
acutangolo
isoscele
ottusangolo
equilatero
rettangolo
Scicchitano Giovanna
PUNTI NOTEVOLI DEL TRIANGOLO
Acutangolo
Ortocentro
Interno
Rettangolo
Vertice
dell’angolo retto
Ottusangolo
Esterno
Incentro
Interno
Interno
Interno
Baricentro
Interno
Interno
Interno
Circocentro
Interno
Punto medio
dell’ipotenusa
Esterno
Scicchitano Giovanna
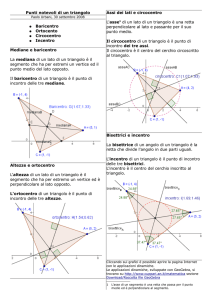
Punti notevoli di un triangolo
Scicchitano Giovanna
Baricentro
Circocentro
Incentro
Ortocentro
Scicchitano Giovanna
Consideriamo un triangolo
Congiungiamo uno dei suoi vertici, ad esempio B,
con il punto medio del lato opposto, cioè AC.
Questo segmento si chiama
mediana relativa al lato AC
A
mediana
B
C
Scicchitano Giovanna
In ogni triangolo c’è una mediana
per ogni lato
Le tre mediane di un triangolo si incontrano
sempre in un punto chiamato baricentro
baricentro
A
•
B
C
Scicchitano Giovanna
A
Il baricentro di
un triangolo
divide ogni
mediana in due
parti che sono
una il doppio
dell’altra.
•
B
•
•
•
C
Il baricentro è l’unico punto di equilibrio di un triangolo
Il baricentro cade sempre all’interno del triangolo
Scicchitano Giovanna
Consideriamo il lato AB di un triangolo qualunque,
tracciamo la perpendicolare passante
per il suo punto medio
Questa retta è l’asse del lato AB
C
asse
A
B
Scicchitano Giovanna
In ogni triangolo c’è un asse per ogni lato
I tre assi di un triangolo si incontrano
sempre in un punto chiamato circocentro,
che è equidistante dai tre vertici
C
circocentro
.
A
B
Scicchitano Giovanna
Il circocentro cade all’interno
di un triangolo acutangolo
B
circocentro
.
C
A
Scicchitano Giovanna
Il circocentro cade all’esterno
di un triangolo ottusangolo
.
B
A
circocentro
C
Scicchitano Giovanna
Il circocentro cade
sul punto medio dell’ipotenusa
di un triangolo rettangolo
C
circocentro
.
A
B
Scicchitano Giovanna
Consideriamo un triangolo
Da uno dei suoi vertici, ad esempio B,
tracciamo la perpendicolare lato opposto, cioè AC.
Il punto
in cui la retta incontra
il lato si dice
piede dell’altezza
A
B
altezza
.
C
Questa retta è l’ altezza relativa al lato AC
Scicchitano Giovanna
In ogni triangolo c’è un’altezza per ogni lato
B
ortocentro
.
C
A
Le tre altezze di un triangolo si incontrano
sempre in un punto chiamato ortocentro
Scicchitano Giovanna
L’ ortocentro cade all’interno
di un triangolo acutangolo
B
ortocentro
.
C
A
Scicchitano Giovanna
B
L’ ortocentro
cade
all’esterno
di un triangolo
ottusangolo
A
C
.
ortocentro
Scicchitano Giovanna
L’ortocentro cade
sul vertice
di un triangolo rettangolo
C
ortocentro
.
A
B
Scicchitano Giovanna
Consideriamo un triangolo
Da uno dei suoi vertici, ad esempio A,
tracciamo la bisettrice, cioè la retta che
taglia in due l’angolo di vertice A
C
bisettrice
A
B
Scicchitano Giovanna
In ogni triangolo c’è
una bisettrice per ogni lato
B
incentro
.
C
A
Le tre bisettrici di un triangolo si incontrano
sempre in un punto chiamato incentro
Scicchitano Giovanna
L’ incentro cade all’interno
di un triangolo acutangolo ed è
equidistante dai tre lati
B
incentro
.
C
A
Scicchitano Giovanna
B
.
incentro
A
L’ incentro cade all’interno
di un triangolo ottusangolo ed è
equidistante dai tre lati
Scicchitano Giovanna
C
L’incentro cade all’interno
di un triangolo rettangolo
ed è equidistante dai tre lati
C
incentro
.
A
B
Scicchitano Giovanna