Presentazione di PowerPoint

transizioni termiche e transizioni radiative
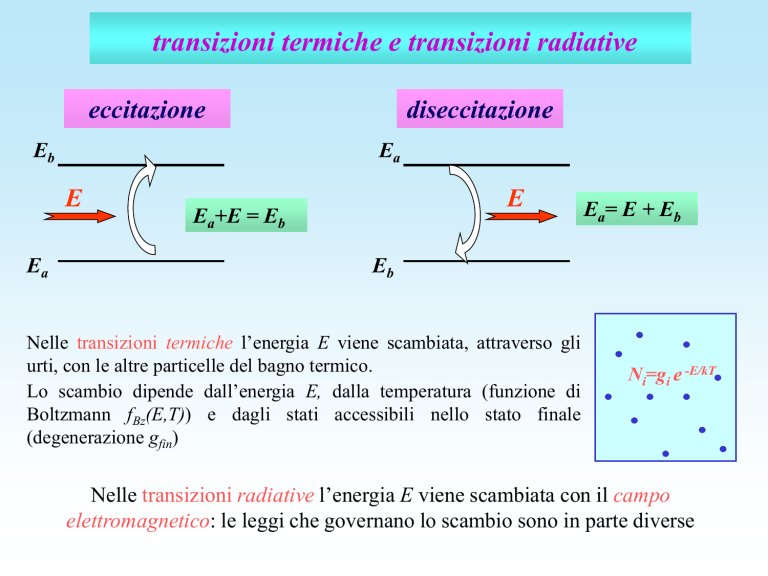
eccitazione
Eb
Ea
E
Ea
diseccitazione
E
Ea+E = Eb
Ea= E + Eb
Eb
Nelle transizioni termiche l’energia E viene scambiata, attraverso gli
urti, con le altre particelle del bagno termico.
Lo scambio dipende dall’energia E, dalla temperatura (funzione di
Boltzmann fBz(E,T)) e dagli stati accessibili nello stato finale
(degenerazione gfin)
Ni=gi e -E/kT
Nelle transizioni radiative l’energia E viene scambiata con il campo
elettromagnetico: le leggi che governano lo scambio sono in parte diverse
transizioni radiative
assorbimento
Eb
Ea
E
Ea
emissione
E
Ea+E = Eb
Ea= E + Eb
Eb
Viene assorbito o emesso un fotone, cioè un quanto di energia del campo elettromagnetico
La probabilità di transizione dipende:
- dalle proprietà della materia (livelli energetici dell’atomo idrogenoide)
- dalle caratteristiche del campo em (intensità del campo alla frequenza giusta
- dalle caratteristiche dell’interazione fra materia e campo
Tutto ciò è oggetto di studio della spettroscopia
sviluppo storico della spettroscopia
L’inizio: il problema del “colore”
Il colore “è contenuto” nella luce o nei corpi?
*1660
Newton studia la rifrazione e scopre gli spettri
 il colore è “contenuto” nella luce
tuttavia … da dove proviene il “colore” delle fiamme?
*1752
Melville scopre gli spettri a righe e descrive la riga gialla della
fiamma sodio  il “colore” è contenuto anche nei corpi?
*1800
Herschel scopre l’infrarosso nella radiazione solare e
Ritter scopre l’ultravioletto nelle proprietà fotochimiche di Ag Cl
sviluppo storico della spettroscopia
dal qualitativo al
quantitativo
*1801
Young calcola la lunghezza d’onda usando dati di Newton
di interferenza da lamine sottili
2d = differenza di cammino fra il raggio (2) e il raggio (1)
(1)
raggio incidente
 si assegna al colore la “lunghezza”  = 2d
(2)
d
*1810  Fraunhofer sviluppa i diffrattometri e misura ben 700 “righe”
fra righe “chiare” (di emissione) e righe “scure” (di assorbimento)
Herschel, Brewster, Foucault associano righe e sostanze
nasce la spettroscopia come tecnica di analisi chimica
sviluppo storico della spettroscopia
*1859 Le leggi di Kirchoff
• la lunghezza d’onda a cui una sostanza emette
dipende unicamente dalla sostanza
• una sostanza assorbe alle stesse lunghezze
d’onda a cui emette
• una sostanza trasparente non emette nel visibile
Inoltre Kirchoff spiega:
- le righe scure nella corona solare
- il puzzle della “riga D” del sodio
- predice l’esistenza del rubidio estrapolando le righe di Na e K
verso la fisica dei “quanti”
sviluppo storico
della spettroscopia
* 1885 la serie di Balmer: f  1/n2 - 1/m2
* 1901 Planck spiega lo spettro di corpo nero e introduce il
“quanto di azione h”
* 1905 Einstein spiega l’effetto fotoelettrico e introduce il
“quanto di luce (fotone)” di energia E=hf
* 1908 Principio di “ricombinazione” di Ritz:
“termine spettrale” a cui è associata una frequenza
f = R Z2 1/n2 (R  3 ·1015s-1)
sviluppo storico della spettroscopia
* 1913 Ipotesi di Bohr sulle transizioni fra stati stazionari:
A causa della proporzionalità tra frequenza ed energia della radiazione (E=hf),
l’emissione o l’assorbimento della radiazione avviene a una frequenza
“sintonizzata” non con la frequenza di rotazione dell’elettrone intorno al
nucleo ma con la differenza di energia fra stati stazionari
assorbimento
emissione
Eb
Ea

stati stazionari

Ea
Eb
Ea+E = Eb
Ea= E
Eb
la condizione di sintonizzazione coincide
con la conservazione dell’energia
+
transizioni
assorbimento

E4
E3
E2
E = E4 - E1 = ER (1-1/16 )= 12,7 eV
E = E3 - E1 = ER (1-1/9 )= 12,1 eV
emissione
E4
E3
E2
E = E2 - E1 = ER (1-1/4 )= 10,2 eV
E1
Serie di Lyman: ultravioletto
E1

transizioni

E5
E4
E3
E2
E = E5 - E2 = ER (1/4-1/25 )= 2,86 eV
E5
E4
E3
E = E4 - E2 = ER (1/4-1/16 )= 2,55 eV
E = E2 - E1 = ER (1/4-1/9 ) = 1,89
eV
E2
H
E1
H
E1
assorbimento
Serie di Balmer: visibile
emissione

sviluppo storico della spettroscopia
la “statistica” della luce
* 1918 Einstein ipotizza l’emissione stimolata e
l’equilibrio radiazione materia
emissione stimolata
Ea



Ea+ E = Eb + 2E
i
due
fotoni uscenti sono
“identici” al fotone incidente
Eb
1954 Gordon, Zeiger e Townes realizzano il
MASER all’ammoniaca
l’interazione radiazione-materia: i tre meccanismi
assorbimento
emissione
Eb
Ea


Ea
Eb
Ea+E = Eb
Ea= E
Eb
Ea



Eb
Ea+ E = Eb + 2E
+
emissione stimolata
descrizione degli stati: la funzione d’onda  (r,t)
risolve l’equazione temporale di Schrödinger



Ψ (r , t )   (r )eiEt /    (r )eit


Ψ ( r , t )
H oΨ ( r , t )  i
t
;   E/
(r) è soluzione dell’equazione stazionaria di Schrödinger
5lm
4lm
3lm
2lm
E5=-0,54 eV
E =0,31 eV  IR
E =-0,85 eV
E =0,75 eV  IR 4
E3=-1,6 eV
E =1,8 eV  rosso
E2=-3,4 eV
E =10 eV  lontano UV
10


Ho ( r )  E ( r )
E1=-13,6 eV
Es.: per l’atomo idrogenoide
p 2 Ze2
Ho 

2m
r
Z2
; En   E R 2
n
come avviene la “transizione”
è causata da un operatore Hint, chiamato “hamiltoniana di
interazione”, associato al campo elettromagnetico, che si
aggiunge all’hamiltoniana imperturbata Ho e “opera” la
trasformazione dallo stato a allo stato b
Eb
assorbimento
Ea+E = Eb


Hin
t
Ea
Ea
Eb
Hin
t


emissione stimolata
Ea+ E = Eb + 2E
a  b
condizioni perché
avvenga la transizione
•sintonizzazione: E = |Ea - Eb|
•accoppiamento: attraverso Hint
l’hamiltoniana di interazione
• è piccola rispetto ad Ho  “perturbazione”
• dipende dal tempo, perché deve modificare l’evoluzione
temporale di  (r,t) dato che l’evoluzione temporale
dello stato a ( exp-ia t) è diversa da quella dello stato
b ( exp-ib t)
• può essere di diversi tipi, la più semplice e importante è
l’interazione di “dipolo elettrico”
 
Hint  er  E
dipolo elettrico
 
 

 i (kr  t ) i (kr  t )
E (r , t )  2Eo cos( k  r   t )  E o (e
e
)
perché un accoppiamento di “dipolo elettrico”?
caso classico macroscopico:
accoppiamento di dipolo elettrico fra antenna e onda e.m.
all’arrivo del campo elettrico oscillante , il dipolo elettrico q(z+-z-) inizia a
oscillare con la stessa frequenza del campo e trasferisce l’energia al circuito
oscillante LC e di qui all’utilizzatore U
z
U

E
q
q

B
descrizione classica nel caso microscopico:
accoppiamento di dipolo elettrico fra l’onda e.m. e le
“antenne microscopiche” nella materia
Esempio di un momento di dipolo elettrico “permanente” molecolare:
il baricentro delle cariche positive (vicino agli ioni H) è spostato
rispetto al baricentro delle cariche negative (vicino allo ione O)
O-momento di dipolo elettrico
O
r  10-10m
-30m  C
H
H
M

6
10
++
2H
il campo e.m. oscillante induce un’oscillazione risonante (sintonizzata) delle
cariche intorno al baricentro
Come si crea un dipolo nel caso di un atomo come l’idrogeno?
Classicamente, istante per istante, c’è un
momento di dipolo elettrico fra la carica
negativa dell’elettrone e quella positiva del
nucleo che si trovano a distanza r
r
…. nel caso quantistico
occorre pensare a una “sovrapposizione di due stati” di diversa energia
che evolvono nel tempo con una diversa legge temporale, ad esempio:
uno stato “1s” (n=1, l=0)
 stato a
e uno stato “2p” (n=2, l=1)
 stato b
la funzione d’onda  (r,t) è in una “sovrapposizione” degli stati a e b che
hanno energia diversa, con ampiezze ca e cb:

 i a t
 i bt
Ψ (r , t )  ca a (r )e
 cb b (r )e
2
2
ca  cb  1



H o a (r )  Ea a (r )  a a (r )
con a , b autofunzioni dell’hamiltoniana Ho:



H o a (r )  Eb b (r )  b b (r )
 NON è uno stato “stazionario”, perché non ha una energia definita, dato che
 a  Ea /  è diverso da b  Eb / 
Le transizioni
Introducendo nell’equazione temporale di
Schrödinger il termine di interazione Hint


Ψ ( r , t )
( H o  H int )Ψ ( r , t )  i
t
la funzione d’onda  (r,t) evolve nel tempo, cioè cambiano nel tempo le
ampiezze ca e cb:
Eb
se Hint fa diminuire ca e aumentare
cb, si ha una transizione dallo stato a
allo stato b (assorbimento)

Hint
assorbimento
Ea
Eb
se Hint fa diminuire cb e aumentare
ca, si ha una transizione dallo stato b
allo stato a (emissione stimolata)

Ea
Hint
emissione stimolata
La condizione di sintonizzazione
Riguarda la frequenza  del campo elettromagnetico.


  i (k r  t )
H int  er E o (e
 e i (k r  t ) )
Applicando Hint alla funzione d’onda  (r,t) si ottengono 4 termini, di cui, se
Eb > Ea, due soli hanno significato, dato che la frequenza  è >0:



  ik r


H int (r , t )  er  Eoe
ca a (r )e i ( a  )t  cb b (r )e i (b  )t
Se   b - a (condizione di sintonizzazione)
-il primo termine ha la stessa evoluzione
temporale dello stato b, quindi descrive la
transizione stato a  stato b con
assorbimento di un fotone
-il secondo termine ha la stessa evoluzione
temporale dello stato a, quindi descrive la
transizione stato b  stato a con emissione di
un fotone

Eb

Hint assorbimento
Ea
Eb

Ea
Hint


emissione
stimolata
La condizione di accoppiamento
Come evolve nel tempo, ad esempio, cb, cioè la probabilità di trovare il sistema
sullo stato b se Eb > Ea? (calcoli dettagliati nella nota 4)
  

cb e
i (   )t
   b (r ) | r  Eo |  a (r )  e b a
t
i
Conviene definire l’operatore “dipolo elettrico” e il suo valore Mba fra gli stati b e a:

 

M ba    b (r ) | er |  a (r ) 


cb
M E
 ba o ei (b  a  )t
t
i
• il valore Mba fra gli stati b e a dell’operatore di dipolo elettrico esprime
l’accoppiamento fra gli stati a e b e il campo elettromagnetico
•integrando fra t=0 e t=to si ottiene l’ampiezza di probabilità che avvenga la
transizione nel tempo to, che è proporzionale a Mba
• il modulo al quadrato |cb(to)|2 dà la frequenza delle transizioni
nell’intervallo di tempo to
Il risultato del calcolo: la probabilità ba
di transizione nell’unità di tempo
sintonizzazione:   |b - a|= ba
Eb
assorbimento
Ea
coefficiente di
assorbimento di Einstein
accoppiamento: Mba
Γ ba 

4 2
3
2
densità spettrale
del campo em
2
M ba  (ba )  Bba  (ba )

Eo2
“regola d’oro” di Fermi
per il calcolo della emissione stimolata, cioè della
transizione opposta dal livello di energia maggiore
al livello di energia minore in presenza del campo
elettromagnetico esterno, basta scambiare gli stati:
il risultato è identico, perché l’operatore di dipolo
elettrico è lo stesso
principio del bilancio dettagliato
 2   ( ) d
0
emissione stimolata
Ea

Eb


emissione spontanea
indipendentemente dalla presenza di un campo
elettromagnetico esterno, il sistema eccitato sul livello
di energia Ea tende a emettere spontaneamente
radiazione tornando sul livello di energia più bassa Eb
Ea
Hint
Eb
in modo simile a
un’antenna che,
mantenuta in
eccitazione
dall’energia della
sorgente, emette
spontaneamente
un campo
elettromagnetico
grazie al buon
accoppiamento che
si realizza tramite
il dipolo elettrico
dell’antenna
emissione spontanea
Ea
probabilità di emissione spontanea per
dipolo elettrico (dalla teoria delle antenne):
sp
Γ 21

4(ba )3
3(c)4
M ba
Hint ba  Ea  Eb
2
Eb
 è proporzionale al quadrato del momento di dipolo elettrico,
come le probabilità di emissione indotta e di assorbimento
 è proporzionale al cubo della frequenza
Esempio: probabilità di
transizione spontanea fra i
livelli n=2 ed n=1
dell’idrogeno, ipotizzando
r21  1 angstrom
4(  21 )3 2  2 4(  21 )3 c c  2
sp
Γ 21 
e r21 
r21
4 1
4
3( c ) c

4(10 ,2eV ) 2 ( 310 8 ms -1 )
3( 210 7 eVm ) 3 137
E2-E1= -3,4-(-13,6)=10,2 eV
vita media sul livello n=2:  = 1/21 0,3 s
3( c )
137
 (1010 m)2  0,3  107 s1
E (eV)
transizione di dipolo elettrico fra uno degli
stati con n=2 e lo stato 1s
sp
Γ 21
4
3
2
-0.85
-1.5
-3.4
2po
Quanto vale l’operatore di
dipolo elettrico?

 

M 21    2 (r ) | er |  1 (r ) 
|M21|
1
-13.6
1s
0
n
4 213  2

M 21
3
3c
0
s
-1
0
1
p
+1
-2 -1 0 +1 +2
2
d
ml
l
“orbitale” atomico 1s
1s
5

1s (r )  R10 (r )Y00
4
funzione d'onda
4
3
 Ce r / ao
3
2
2
funzione d’onda
1
1
0
-4.00
simmetrica
-3.00
-2.00
-1.00
0.00
1.00
z (angstrom)
2.00
3.00
4.00
z
per inversione degli assi:
x-x
y-y
z-z
segno della funzione d’onda
in questa zona, non della
carica elettrica!
2pz
“orbitale” atomico 2po
0,15

 2 po (r )  R21 (r )Y10
funzione d'onda
0,10
0,05
 Cre  r / 2ao cos 
0,00
 Cze  r / 2ao
-0,05
-0,10
funzione d’onda
-0,15
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
z (angstrom)
3
4
5
6
7
8
antisimmetrica
per inversione degli assi:
x-x
y-y
z
z-z
segno della funzione d’onda nella
zona, non della carica elettrica!
M 1zs,2 p z 



1s (r ) | ez |  2 p z (r )  e  R10 (r ) R21 (r )r 3dr
0
2
 d  cos
0
0,15
funzione d'onda
2po
1s
2po
z è l’operatore che trasforma la funzione
d’onda 2po nella funzione d’onda 1s
0,00
-0,05
-0,10
l’integrando
-0,15
-8
-7
-6
-5
-4
-3
-2 -1 0
1
2
1s
z (angstrom)
3
4
5
6
1.6
1.4
1.2
funzione d'onda
1
( )d
calcolo del
momento di
dipolo elettrico
2po  1s
ez
2pz
0,05
2
z = r cos 
Mz = e z
0,10
1
1s
1.0
0.8
0.4
0.2
-6.0
-4.0
-2.0
0.0
2.0
z (angstrom)
-è sempre positivo, perché 1s e 2po hanno
“parità opposta” (1s è pari, mentre 2po è
dispari )
8
- è grande per quei valori di z per i quali 1s
e 2po sono entrambe diverse da zero
0.6
0.0
-8.0
7
4.0
6.0
8.0
z è l’operatore che trasforma la funzione
d’onda 2po nella funzione d’onda 1s;
in coordinate sferiche z = r cos 
z = r cos 

2
0
0


M 1zs,2 po  1s (r ) | ez |  2 po (r )  e  R10 (r ) R21 (r )r 3dr

1
calcolo del
momento di dipolo
elettrico 2po  1s
2po
d  cos 2 ( )d cos
ez
1
1s
- il momento di dipolo elettrico è diverso da zero solo
se gli integrali sugli angoli  e  sono diversi da zero
- ciò si realizza in questa transizione perché
l = 1 nello stato 2po , l = 0 nello stato 1s
ml = 0 in entrambi gli stati
regola di selezione:
l =1
 ml = 0
Transizioni
2p+ 1s
2p- 1s
Per indurre la transizione 2p+ 1s oppure 2p- 1s
occorre un “operatore” che operi anche una
trasformazione della dipendenza azimutale  della
funzione d’onda, dato che la dipendenza è diversa
nelle due funzioni d’onda:

 1s (r )  R10 (r )Y00  Ce r / ao

 2 p  (r )  R21 (r )Y11  CR21 (r ) sen  ei
Occorre ricorrere a uno degli altri componenti
dell’operatore di dipolo elettrico, perché l’operatore z
non opera sull’angolo 
2p-
1s
M è un “operatore vettoriale” , cioè è composto da 3 operatori:


M 21  er21
x
M 21
 e x21
y
M 21
 e y21
z
M 21
 e z 21
2p+
l’operatore di dipolo elettrico
in coordinate sferiche:
z  r cos
x  r sen  cos   r sen  (e
i
y  r sen  sen   r sen  (e
i
e
 i
e
)/2
r  r sen  ei
)/2
r  r sen  e i
 i
r- è l’operatore che trasforma la funzione d’onda 2p+ nella funzione d’onda 1s:

2
0
0


M 1s,2 p  1s (r ) | er |  2 p (r )  e  R10 (r ) R21 (r )r 3dr
l’integrazione sull’angolo  dà 2;
anche l’integrazione su cos è
diversa da zero, perché l’integrando è
una funzione pari in cos

1
ei e i d  sen 2 ( )d cos
1
regole di selezione:
l =1
 ml = 0,  1
E (eV)
4
3
2
transizioni permesse per dipolo elettrico:
2po 1s ; 2p+ 1s ; 2p- 1s
-0.85
-1.5
-3.4
2p-
er+
1
-13.6
ero
2p+
3 
2
4

21
sp
Γ 21 
M 21
3
3c
er-

 

M 21    2 (r ) | er |  1 (r ) 
1s
0
n
2po
0
s
-1
0
1
p
+1
-2 -1 0 +1 +2
2
d
ml
l

2
1
0
0
1


M 1zs,2s  1s (r ) | ez |  2s (r )  e  R10 (r ) R20 (r )r 3dr
ez
 d  cos d cos
esempio di
transizione
proibita:
2s  1s
2s
7.0
6.0
funzione d'onda
5.0
4.0
l’integrazione su cos dà risultato
nullo, perché l’integrando è una
funzione dispari in cos , come
atteso in base alla
3.0
2s
2.0
1.0
0.0
-1.0
-2.0
-3.0
-10.0
-5.0
0.0
5.0
10.0
z (angstrom)
1s
1.6
1.4
funzione d'onda
1.2
1s
1.0
0.8
0.6
0.4
0.2
0.0
-8.0
-6.0
-4.0
-2.0
0.0
2.0
z (angstrom)
4.0
6.0
8.0
regola di selezione:
l =1
E (eV)
Intensità della riga spettrale
sp
Γ 23
4 -0.85
3 -1.5
2 -3.4
3s
3p-
3po
3p+
2s
2p-
2po
2p+
costante di
proporzionalità
sp  Ea / k BT
I ab  CΓ ab
e
probabilità di transizione
spontanea per unità di
tempo dal livello a al
livello b

4(23 )3
3(c)4
M 23
2
3d-2 3d-1 3do 3d+1 3d+2
ij  aib j
probabilità di occupazione
del livello di energia Ea
(fattore di Boltzmann)
regola di selezione
per raggiungere lo
stato j del livello b
a partire dallo stato
i del livello a