12-Sforzo_2

Fratture tensili e da taglio
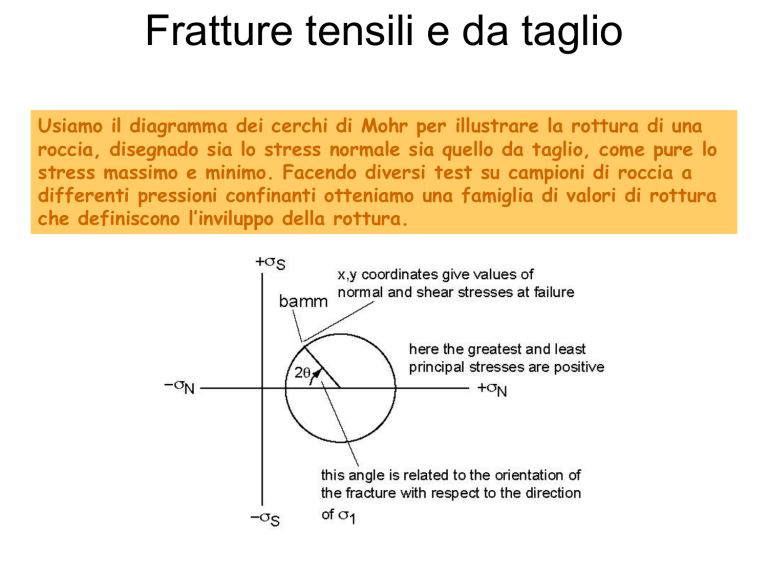
Usiamo il diagramma dei cerchi di Mohr per illustrare la rottura di una
roccia, disegnado sia lo stress normale sia quello da taglio, come pure lo
stress massimo e minimo. Facendo diversi test su campioni di roccia a
differenti pressioni confinanti otteniamo una famiglia di valori di rottura
che definiscono l’inviluppo della rottura.
Fratture & fratture da taglio in
laboratorio
Ci sono 2 tipi di test per valutare la
resistenza di una roccia:
1) Test per la resistenza tensile: il
campione è tirato lungo il suo asse (s3)
con o senza pressione confinante
applicata ai suoi lati (s1 = s2) fino alla
rottura.
2) Test per la resistenza alla
compressione: il campione è
compresso lungo il suo asse (s1) con o
senza pressione confinante applicata
ai lati (s2 = s3) fino alla rottura.
Alla rottura, I valori degli stress principali
sono annotati e così l’orientazione del
piano di rottura.
Questi dati sono riportati nel cerchio di Mohr.
Un singolo esperimento
produrrà un singolo dato che
descrive gli stress da taglio e
normale (sn, ss) rispetto al piano
di rottura nell’istante di rottura.
Possono essre effettuati un
numero di test simili a differenti
pressioni confinanti e creare
quindi una serie di dati.
L’insieme dei punti mi definisce
una linea chiamata inviluppo
della rottura.
L’inviluppo separa lo spazio di
Mohr in due regioni: una stabile
dove non c’è rottura, l’altra dove
non possono esistere rocce
indeformate.
Ogni punto lungo l’inviluppo
rappresenta la rottura della
roccia a differenti stress
differenziali:
Quindi ogni cerchio verso la
destra è sempre più grande
Rx failure (fracture) at a
specified s3 and s1).
Test della resistenza tensile
 Le rocce sono generalmente molto deboli alla tensione.
Esse sono dalle 2 alle 30 volte più forti alla compressione.
Ricorda: in geologia strutturale gli stress tensili sono negativi
(-) mentre quelle compressivi sono positivi(+).
 Possiamo rappresentare la rottura tensile nello spazio di
Mohr ed avere un idea di come la legge di rottura tensile
funziona.
Test della resistenza tensile
Per primo confrontiamo questo test con quello della compressione: le rocce
sono molto deboli alla tensione. Il rapporto tra resistenza alla tensione e
quella per la compressione è 2:1 fino a superare 1:30.
Se volete rompere un bastoncino lo potete piegare e lungo l’arco esterno
agiranno stress tensili mentre in quello interno compressivi, dopo un po’ il
bastoncino si romperà nella parte esterna.
 Lo stato di stress proprio prima dell’esperimento è s1 = s2 = s3 = 0. Questo è
rappresentato da un singolo punto dove non c’è stress differenziale.
 come lo stress tensile cresce parallelo alla lunghezza del campione così lo
stress differenziale cresce.
Crescita
degllo stress
tensile con
crescita del
diametro del
cerchio.
All’inizio dell’esperimento non c’è nessun stress
differenziale (stato di stress idrostatico).
La rottura tensile avviene semplicemente quando la
resistenza tensile della roccia è superata e il piano di
frattura è perpendicolare allo stress tensile:
Lo stress tensile aumenta parallelamente alla
lunghezza del campione. Come lo stress
differenziale cresce così aumenta il diametro del
cerchio di Mohr.
Lo stress perpendicolare all’asse del campione è
s1.
Durante il test esssndo lo stress tensile negativo
deve essere per forza il minimo strss (s3).
Quando la resistenza tensile è superata allora la roccia si
rompe perpendicolarmente alla direzione della tensione
(s3).
Si forma una frattura di modo1
La legge della
resistenza tensile è:
s3 = To
Una roccia si romperà attraverso fratture di modo1 se
l’intensità dello sforzo minimo (s3) sarà uguale o supera
la resistenza tensile della roccia.
La frattura di modo 1 è parallela a s1 e perpendicolare a s3.
Nello spazio di Mohr il raggio che connette il centro del cerchio dello
stress differenziale con il punto di rottura giace sull’asse x.
Test della resistenza tensile e compressiva
Possiamo anche eseguire un test triassiale 8con una
quantità piccola di pressione confinante applicata ai fianchi
del campione mentre applichaimo lo stress tensile lungo
l’asse.
Esploriamo le
relazioni tra lo stress
differenziale,
pressione confiante
e resistenza alla
fratturazione di una
roccia in
compresione.
10 MPa
Se iniziamo l’esperimento con una pressione
confinante di10 Mpa allora aumenrtiamo lo stress
tensile parallelo alla lunghezza del campione.
Quando la resistenza tensile della roccia è superata
allora il campione si rompe perpendicolarmente alla
direzione di tensione (s3).
Si forma una frattura di modo 1.
10 MPa
Come il test va avanti lo stress differenziale (s1 s3) cresce (cioè il diametro del cerchio di Mohr)
fino alla fratturazione.
Ora iniziamo l’esperimento con una pressione
confinante di 40 MPa.
Se la pressione confinante variano tra If the
s1 = 3 a 5To (cioè tra 3 e 5 volte la resistenza
tensile di un’arenaria),
L’inviluppo si appiattisce leggermente
passando per l’asse dello stress di taglio e la
sua forma diventa parabolica (dark line).
Si formano due fratture
coniugate ibride (tensili
e da taglio)
Rottura sotto stress compressivi
 al crescere della
pressione confinante
(s3), abbiamo bisogno
di far crescere lo
stress differenziale
(s1-s3).
 la crescita dello
stress differenziale è
mostrato dal cambio
nel diametro del
cerchio di Mohr.
Il criterio di rottura di Coulomb
s c = s 0  tan  (s N )
Modelli dinamici e meccanici
sviluppati da Coulomb (1773) e
Mohr (1900).
Il criterio descrive l’altezza e
l’inclinazione dell’inviluppo della
rottura per rocce in
compressione.
sc = so + sNtan
 = angolo di attrito interno
tan = coefficiente di attrito
interno
sc = stress di taglio critico per la
fratturazione
so = coesione
sN = stress normale
Questi test definiscono
l’inviluppo della
fratturazione per una
particolare roccia
 Tutti gli stress normali e
di taglio sotto
all’inviluppo sono stabili
e nessuna frattura si
produce.
 Tutti gli stress sopra
l’inviluppo produrranno
la fratturazione
 quando il cerchio di
Mohr diventa tangente
all’inviluppo allora il sc
in quel punto causa una
frattura.
 nessun altra frattura si
produce per altre
combinazioni di sc sul
cerchio.
Relazione tra stress e
fratturazione
Criterio di rottura di Coulomb:
s c = s 0  tan  (s N )
L’inclinazione e la linearità
dell’inviluppo rivela che la
resistenza alla
compressione di una roccia
aumenta con l’aumentare
della pressione confinante.
L’angolo di inclinazione è
chiamato angolo di attrito
interno ().
L’inviluppo è chiamato
l’inviluppo di Coulomb
 Nel caso specifico il punto
di rottura sull’inviluppo di
Coulomb formìnisce i
seguenti valori dei moduli
sN = 43 and ss = 47 MPa.
 in termini del criterio di
rottura il valore dello stress
di taglio di 47 MPa è lo
stress critico di taglio (sc)
necessario per la
fratturazione.
 parte della sua intensità è
la coesione (s0) letta
direttamente come intercetta
dell’inviluppo con l’asse y
Il resto dello stress critico di
taglio (sc) è lo stress richiesto
per superare l’attrito interno e
quindi produrre la frattura.
Questa componente equivale a:
sN tan
Questo valore è espresso in
termini di stress normale agente
sulla frattura e dell’angolo di
attrito interno che è
l’inclinazione dell’inviluppo.
La coesione (s0) è una
piccola parte dello stress
critico di taglio
La maggior parte delle
fratture di taglio si
formano quando lo stress
di taglio sul piano di
frattura raggiunge un
livello di oltre il 50% dello
stress normale agente sul
piano.
s c = s 0  tan  (s N )
Note change in slope
Cosa succede con pressioni
confinanti più alte?
A più alte pressioni confinanti il criterio
di rottura di Coulomb non è valido.
La roccia si comporta in un modo
meno fragile.
La linea dell’inviluppo diventa concava
verso il basso e l’inviluppo ha
un’inclinazione minore.
Il criterio di Von Mises descrive il comportamento al di
sopra della transizione fragile-duttile
Quando la soglia di stress critico è superata la roccia si
deformerà lungo dei piani di taglio duttili orientati a 45°
da s1.
Measured values of
tensile strength,
cohesive strength,
and internal friction
for a few rock types.
Rock failure envelope
for a rock marked by low
tensile strength, low
cohesive strength, and
low internal angle of
friction.
Rock failure
envelope for a rock
marked by high
tensile strength,
high cohesive
strength, and high
internal angle of
friction.