Immagini reali e virtuali - miraggi
La retina dell’occhio umano intercetta i raggi luminosi riflessi dall’oggetto che si sta guardando. Tale
procedura funziona anche se i raggi di luce non provengono direttamente dall’oggetto. Ad esempio,
stando davanti ad uno specchio piano, si osservano degli oggetti (o anche noi stessi) che ci appaiono
dietro lo specchio. Tali oggetti non sono realmente dietro lo specchio, ma ai nostri occhi appaiono
come se lo fossero. Le immagini di tali oggetti sono dette immagini virtuali, perché esistono soltanto
nel nostro cervello ma noi diciamo che esistono nel luogo in cui le abbiamo percepite.
Le immagini reali sono riproducibili su una superficie, come un film al cinema. provenienti non vede
Le immagini virtuali non esistono in nostra assenza, mentre le immagini reali sono indipendenti dalla
nostra presenza.
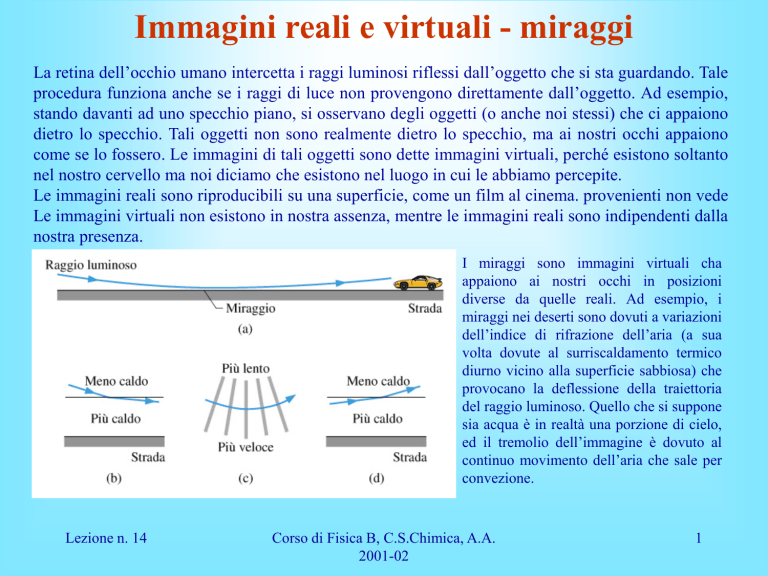
I miraggi sono immagini virtuali cha
appaiono ai nostri occhi in posizioni
diverse da quelle reali. Ad esempio, i
miraggi nei deserti sono dovuti a variazioni
dell’indice di rifrazione dell’aria (a sua
volta dovute al surriscaldamento termico
diurno vicino alla superficie sabbiosa) che
provocano la deflessione della traiettoria
del raggio luminoso. Quello che si suppone
sia acqua è in realtà una porzione di cielo,
ed il tremolio dell’immagine è dovuto al
continuo movimento dell’aria che sale per
convezione.
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
1
Specchi piani
Una superficie riflettente piana è chiamata specchio piano. I raggi luminosi provenienti dal punto O sono riflessi ma i
loro prolungamenti oltre lo specchio si incontrano nel punto I, detto immagine di O. L’immagine è virtuale in quanto i
raggi luminosi non passano per I. I triangoli rettangoli aOb e aIb sono uguali per cui Ib = Ob ovvero p = -i (si
definiscono p = Ob = distanza oggetto-specchio e i=Ib = distanza immagine-specchio; si noti che le direzioni di p ed
i sono opposte, di qui il segno -). Un osservatore che guarda l’immagine riflessa di O ad un angolo q vedrà tale
immagine non nel punto O ma nel punto I. Inoltre, soltanto una piccola porzione di specchio è sufficiente per la riflessione dell’immagine dell’oggetto puntiforme O.
L’immagine riflessa da un oggetto esteso, invece, ha
la stessa altezza e lo stesso orientamento
dell’oggetto.
Si consideri una persona alta H con gli occhi distanti
L dalla sommità della testa e posta alla distanza p
dallo specchio. Quanto deve essere alto lo specchio
(Zmin) affinchè la persona possa vedersi
completamente?
La risposta è: H/2
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
2
Specchi sferici
Specchio concavo
Incurvando uno specchio piano in modo concavo o convesso, si può
osservare che il centro di curvatura si sposta da al punto C,
l’estensione visiva si è ridotta e l’immagine appare ingrandita o
rimpicciolita.
Inoltre si introduce il fuoco o distanza focale dello specchio,
definito come il punto di convergenza dei raggi (o dei loro
prolungamenti) paralleli all’asse ottico.
Nello specchio concavo la posizione del fuoco F (così come quella
del centro di curvatura C) è reale, nello specchio convesso è virtuale.
In entrambi i casi
f = r / 2.
Specchio convesso
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
3
Equazione dei punti coniugati
L’immagine
I
dell’oggetto
puntuale O posto sull’asse di uno
specchio sferico concavo il cui
centro di curvatura è C si trova
anch’essa sull’asse ottico. Si
tracci il raggio Oa. La legge di
Snell stabilisce che gli angoli di
incidenza e riflessione q sono
uguali e simmetrici rispetto a Oa. Guardando i triangoli OaC e CaI:
b=a+q
g=a+2q
da cui si può ricavare la relazione
a+g=2b
I tre angoli a, b e g possono essere espressi in funzione dell’arco di
circonferenza ac:
a ac / cO = ac / p
1 1 1 2
+ = =
b = ac / cC = ac / r
g ac / cI = ac / i
p
i
f
r
Si noti come l’immagine di un oggetto possa essere reale, virtuale o
posta all’infinito a seconda che l’oggetto sia posto prima, dopo o sul
fuoco.
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
4
Ingrandimento e ricostruzione grafica dell’immagine
L’ingrandimento trasversale è definito come
|m| = h’ / h
ovvero come
m = -i / p
Le immagini possono essere costruite graficamente usando due dei seguenti quattro raggi:
1. Raggio
parallelo
all’asse
ottico
(riflettendosi
passa
per il fuoco)
2. Raggio che passa per
il fuoco prima di
riflettersi (è parallelo
all’asse ottico)
3. Raggio passante per il
centro di curvatura (è
riflesso su se stesso)
4. Raggio incidente nel
vertice dello specchio
(è simmetrico rispetto
all’asse focale)
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
5
Superfici rifrangenti sferiche
Si considerano superfici di separazione sferiche di raggio r. L’immagine prodotta è reale o
virtuale a seconda delle caratteristiche dei due mezzi e del valore del raggio di curvatura. Il
raggio rifratto si avvicina alla (allontana dalla) normale alla superficie entrando in un
mezzo con indice di rifrazione maggiore (minore).
Se il raggio nel mezzo 2 si allontana dall’asse allora l’immagine si forma sul suo
prolungamento nel mezzo 1.
Le immagini sono definite virtuali quando si formano dalla stessa parte dalla quale
proviene il raggio (cioè dove si trova l’oggetto). Per i raggi di curvatura, la convenzione è
che sono assunti positivi quando l’oggetto si affaccia su una superficie rifrangente
convessa.
Elenco dei sei possibili casi di formazione delle
immagini: in tutti i casi la sostanza con indice di
rifrazione n maggiore è colorata
Caso (a) concava, p > |f|
Caso (b) convessa, p > |f|
Caso (c) concava, p < |f|
Caso (d) convessa, p < |f|
Caso (e) concava, p < |f|
Caso (f) convessa, p < |f|
L’immagine è REALE solo nei casi a, b.
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
6
Formula per le superfici rifrangenti
Il raggio Oa si riflette ed è rifratto nel punto a. Gli angoli di incidenza e rifrazione q1 e q2 sono legati
dalla legge di Snell:
n1 sin q1 = n2 sin q 2
n1q1 = n2q 2
o per piccoli angoli
Inoltre, guardando i triangoli AaC e CaI, si ha:
q1 = a + b e b = q 2 + g I tre angoli a, b e g possono essere espressi in funzione dell’arco ac come:
a
ac
;
p
b=
ac
;
r
g
n1a + n2g = n2 n1 b
ac
;
i
e sostituendo nella relazione precedente, si trova:
Ricordando la legge di Snell semplificata, si arriva alla formula
n1 n2 n2 n1
+ =
p i
r
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
7
Formula dei costruttori di lenti
Una lente si può considerare formata da due superfici rifrangenti affacciate con lo stesso asse ottico.
Nel seguito verranno esaminate solo le lenti sottili (spessore h piccolo rispetto alle distanze in gioco: i,
p, r1, r2, f) e verranno presi in esame solo i raggi parassiali (che formano angoli piccoli rispetto
all’asse ottico).
L’immagine I’ dell’oggetto O’ rispetto alla prima superficie, per la quale n1=1 (aria) e n2=n è:
1 n n 1
=
Essa può essere considerata come oggetto O” per la seconda superficie distante L
p' i'
r'
dalla prima e tra le quali è inserito il materiale (indice di rifrazione n2=n)
n 1 1 n
+ =
p" i"
r"
Essendo
p" = i '+ L
si ottiene:
1 1
1 1
+ = n 1
p ' i"
r ' r"
Tale espressione può essere semplificata nell’ipotesi di lente sottile (L<<p,i,r) ottenendo:
1 1 1
+ =
p i f
Dove il fuoco f è
definito da:
Lezione n. 14
1
1 1
= n 1
f
r ' r"
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
8
Lenti sottili
La formula della lente sottile è valevole anche se la lente è immersa in un mezzo il cui indice di
rifrazione è nmezzo, avendo l’avvertenza di sostituire a n il valore n / nmezzo.
Una lente composta da due superfici rifrangenti convesse fa convergere i raggi paralleli all’asse
ottico provenienti da sinistra nel fuoco F2 e quelli provenienti da destra nel fuoco F1. In questo caso i
fuochi F1 e F2 sono reali (i raggi passano per i fuochi), per cui f > 0, e la lente è convergente.
Una lente composta da
due
superfici
rifrangenti concave fa
divergere
i
raggi
paralleli all’asse ottico.
I prolungamenti dei
raggi provenienti da
sinistra convergono nel
fuoco F2 mentre quelli
provenienti da destra
convergono nel fuoco
F1. In questo caso i
fuochi F1 e F2 sono
virtuali (i raggi non
passano per i fuochi),
per cui f < 0, e la lente
è divergente.
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
9
Esempi di immagini create da lenti
L’immagine di un oggetto per cui p > f in una lente convergente è reale (posta dalla parte opposta
rispetto all’oggetto) e capovolta.
L’immagine di un oggetto per cui p < f in una lente convergente è virtuale (posta dalla stessa parte
rispetto all’oggetto) e dritta.
L’immagine di un oggetto in una lente divergente è sempre virtuale e dritta.
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
10
Ricostruzione grafica dell’immagine per oggetti non puntiformi
L’immagine di qualsiasi punto di un oggetto non puntiforme può essere ricostruita
graficamente tracciando due dei seguenti tre raggi e vedendo dove si incontrano:
1) Raggio parallelo all’asse ottico e passante (o il cui prolungamento passa) per F2;
2) Raggio passante (o il cui prolungamento passa) per il fuoco F1: esso emergerà dalla
lente parallelo all’asse ottico;
3) Raggio passante (o il cui prolungamento passa) per il centro della lente, che non viene
deviato.
Per le lenti divergenti, occorre sempre considerare i prolungamenti dei raggi.
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
11
Sistemi ottici
Nel caso si abbia a che fare con sistemi ottici
formati da due o più lenti, occorre procedere in
serie lente per lente procedendo come se le altre
lenti non ci fossero, e considerare la posizione
dell’immagine di una lente come oggetto per la
lente successiva.
Per quanto riguarda i segni, se la posizione
dell’oggetto viene a trovarsi dalla parte opposta
rispetto alla sorgente di luce, la sua distanza va
presa con il segno negativo.
L’ingrandimento complessivo è pari al prodotto
degli ingrandimenti di ogni singola lente:
N
m = mi
i =1
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
12
Lente d’ingrandimento
L’occhio umano è in grado di mettere a fuoco un oggetto sulla retina con la massima precisione ad
una distanza di circa 25 cm, detta distanza della visione distinta o punto prossimo Pn. La
dimensione dell’oggetto vista dall’occhio dipende dall’angolo q. Per punti O più vicini di Pn, q è
maggiore ma l’oggetto non è più a fuoco. Ponendo una lente in modo che la posizione dell’oggetto O
sia prossima al fuoco F1 della lente, l’immagine I si forma in un punto più lontano di Pn per cui è a
fuoco.
Definito l’ingrandimento angolare come mq = q’ / q nel caso in questione essendo q h / 25 cm e
q’ h / f si ha:
mq =
25 cm
f
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
13
Microscopio
Composto da un oculare (foc) e da un obbiettivo (fob). Il sistema ottico del microscopio fa sì che
l’immagine I dell’oggetto O rispetto all’obbiettivo si formi sufficientemente vicino al fuoco F1’
dell’oculare, di modo che l’immagine I’ rispetto all’oculare si formi in un punto più lontano del
punto prossimo e sia ingrandita (si agisce sulla distanza s).
La grandezza s (distanza tra i due fuochi F2 e F1’) è detta tiraggio e normalmente nei telescopi
s>>fob per cui si ha 2 fob + s s mentre l’oculare agisce come una lente. I due ingrandimenti sono:
mob =
i
s
p
f ob
Lezione n. 14
moc =
25 cm
f oc
m = mob moc
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
s 25 cm
f ob f oc
14
Telescopio rifrattore
Il telescopio rifrattore ha solo un obbiettivo ed un oculare. Il sistema è costruito in
modo che le distanze focali delle due lenti siano coincidenti (F2 F1’).
L’immagine dell’oggetto O posto a distanza quasi infinita e visto sotto l’angolo qob
ad occhio nudo viene fatta convergere nel fuoco F2 F1’ e vista dall’occhio sotto
l’angolo qoc (invertita). L’ingrandimento (angolare) vale
mq = - fob / foc
Lezione n. 14
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
15