i 1 - Sezione di Fisica

Corrente elettrica
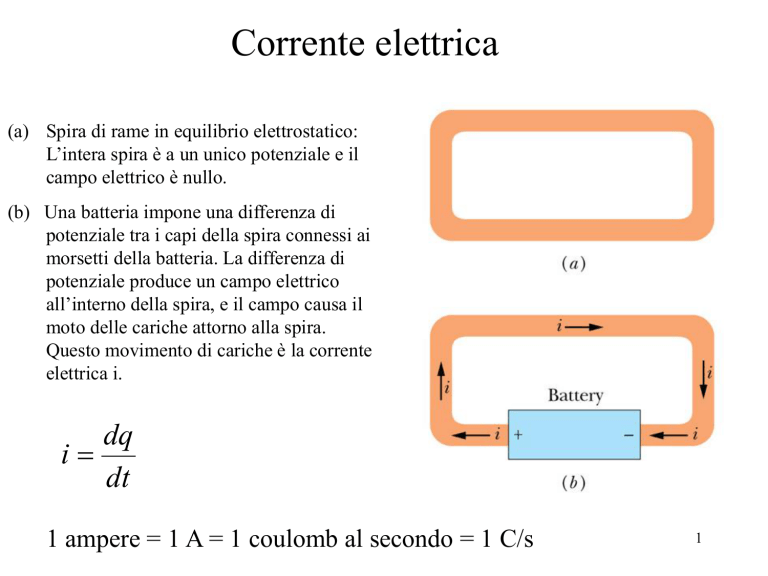
(a) Spira di rame in equilibrio elettrostatico:
L’intera spira è a un unico potenziale e il
campo elettrico è nullo.
(b) Una batteria impone una differenza di
potenziale tra i capi della spira connessi ai
morsetti della batteria. La differenza di
potenziale produce un campo elettrico
all’interno della spira, e il campo causa il
moto delle cariche attorno alla spira.
Questo movimento di cariche è la corrente
elettrica i.
dq
i
dt
1 ampere = 1 A = 1 coulomb al secondo = 1 C/s
1
Verso della corrente
Convenzione (storica!):
Il verso della corrente è quello nel quale si muoverebbero le cariche positive, anche se gli
effettivi portatori di carica sono negativi e si muovono in senso opposto.
Gli elettroni in un filo si muovono in modo casuale ad alte velocità (ca 106 m/s),
un campo esterno impone un movimento di deriva, che tipicamente è molto basso (velocità
di deriva vd , ca 10-4 m/s)
Questa deriva produce la corrente elettrica
Se la densità di carica è
n e (C/m3)
otteniamo la densità di corrente


J  n  e vd
 
E la corrente elettrica risulta come i   J  dA
spesso
iJA
2
In un acceleratore di particelle circolare con un raggio R di 35m, un fascio di 1010
protoni circola con velocità costante pari a c. Calcolare la corrente cosi’ prodotta.
La carica che passa ad ogni giro nell’ acceleratore è:
q  1010 1,6 1019 C  1,6 109 C
2R
Tale carica passa in un tempo pari a: T 
 7,3 10 7 s
c
La corrente sarà:
q 1,6 109
3
i 

2
,
19

10
A
7
T 7,3 10
3
Se si applica la stessa differenza di potenziale tra le estremità di bacchette di rame e di
legno geometricamente simili, ne risultano correnti assai diverse.
=> Resistenza elettrica
“La resistenza di un conduttore tra due punti si determina applicando una
differenza di potenziale V tra quei punti e misurando la corrente i che si
stabilisce.
V
R
i
1 ohm = 1 W = 1 volt/ampere = 1 V/A
Un conduttore la cui funzione in un circuito è quella di fornire una resistenza è detto
resistore
Resistività di un materiale:
campo elettrico/densità di corrente

Unità di  : (V/m) / (A/m2) = (V/A)m = Wm
E
V
L
J
E VL
  i
J
A
E
J
V diff.di pot.
i
A
A
L
 R
A
i
L
4
R
V
i
Definisce la “resistenza”, ma può anche essere visto come descrizione di una
proprietà di un corpo:
Se per un corpo è vero che
R
V
i
si dice, che obbedisce la legge di Ohm.
Di grande importanza sono I semiconduttori e I superconduttori (devono essere discussi
però in una lezione specialistica):
Superconduttori: a temperature basse la resistività può sparire.
Semiconduttori, per esempio silicio: silicio puro ha una alta resistività ( 3 103 W  m
paragonato con 2 10 8 W  m per rame), però la sua resistività può essere ridotta in modo
controllato (drogaggio).
5
dE  dq V  i  dt V
dE
P
 i V
dt
J
 J   C
1V  A  1   1   1  1W
s
 C  s 
Per resistenza R:
V2
P i R 
R
2
2
Per correnti alternate: P  I qm
R
2
Valore quadratico medio della corrente i
I qm
6
a) Quanta corrente è presente in una lampadina da 60 Watt connessa ad una
differenza di potenziale di 120 V?
b) Quanto à la resistenza della lampadina?
a) La potenza è: P = 60 W = I x V = I x 120
cosi’ che I = ½ Amp (A)
b) Vale inoltre: V = I R 120 V = ½ A x R
cosi’ che R = 240 W, o R = V/I
a) Se una lampadina da 3 V ha una resistenza di 9 ohms, quanta corrente può
portare?
b) Se una lampadina è attraversata da una corrente di 2 A quando connessa ad un
circuito di 120 V, qual’è la sua resistenza?
a) I = V / R = 3 V / 9 W = 1/3 Amps
b) R = V / I = 120 V / 2 A = 60 W
7
Resistenze in serie
i
V  V1  V2  V3  i  R1  i  R2  i  R3  i  ( R1  R2  R3 )
R1
B
R2
V
V  i  Req
 Req  R1  R2  R3
R3
V
B
Req
i
8
Resistenze in parallelo
B
1
1
1 
i  i1  i2  i3  V   
 
 R1 R2 R3 
V
i3
R1
V
i
Req

1
1
1
1
 

Req R1 R2 R3
R2
V
R3
B
Req
i
9
Un resistore di 4W e un resistore di 6W sono collegati in parallelo, e ai capi del
sistema è applicata una differenza di potenziale di 12 V. Si trovi:
a) L’ intensità di corrente in ciascun resistore
b) La potenza dissipata in ciascun resistore
a) Per ottenere l’ intensità di corrente in ciascun resistore, si tenga presente che
la caduta di potenziale ai capi di ciascun resistore è 12 V. Denotando con I1 la
intensità di corrente che nel resistore di 4W e con I2 quella nel resistore di 6W
si ha:
V  I1 R1  I1 (4W)  12V
12V
I1 
 3,0 A
4W
e
I2 
12V
 2,0 A
6W
b) La potenza dissipata nei resistori è:
P1  I12 R1  3,0 A (4W)  36W
2
P2  I 22 R2  2,0 A (6W)  24W
2
10
Un resistore di 4W e un resistore di 6W sono collegati in parallelo, e ai capi del
sistema è applicata una differenza di potenziale di 12 V. Si trovino:
a) la resistenza equivalente
b) l’ intensità di corrente totale
a)
Per la resistenza equivalente Req si calcoli:
1
1
1
3
2
5





Req 4W 6W 12W 12W 12W
12W
 2,4W
ossia: Req 
5
b) Perciò l’ intensità di corrente totale è:
V
12V
I

 5A
Req 2,4W
11
Per misurare la corrente: amperometro
Per misurare la corrente in un filo, si deve generalmente interrompere il filo e
inserire l’amperometro, in modo che la corrente da misurare passi attraverso lo
strumento. La resistenza dell’amperometro deve essere piccola
Per misurare la differenza di potenziale:
voltmetro
per trovare la differenza di potenziale tra due
punti nel circuito, gli elettrodi del voltmetro
devono essere collegati ai due punti, senza
interrompere il circuito.
La resistenza del voltmetro deve essere
grande
12
Circuiti RC
interruttore
VR  R  i
Resistenza R
batteria
VB
q
VC 
C
Condensatore C
13
 
d ex
 ex
dx
Ci ricordiamo:

ab 
 a(b)  b
a  b  a  b  a  b


d e   x

   e  x
dx


d   e   x

   (  e   x )
dx
perche
d
0
dt
(I) È un caso particolare di (II), altri soluzioni non esistono
14
Detto in modo diverso:
f (t )    e  t
e’ una soluzione di
df (t )
   f (t )  0
dt


d   e   x
   (  e   x )
dx
  (  e t )      e  t  0
15
e
 t 

 
f (t )     1  e




1
è soluzione di
df (t )

   f (t )  
dt
df (t )    t   

    e
dt
 

t  
   t   
1

       1  e   
     e
 




t  
t  




 e



1

e







16
VB
Scarica di un condensatore:
VR  VC
 R i 
q
0
C
o
df (t )
   f (t )  0
dt
f (t )    e  t
DV
 VR  VC  0
 R
dq q
 0
dt C
dq
1

q  0
dt R  C
 q(t )  q0  e
t
RC
q0
dq
t
 i (t ) 

 e RC
dt
R C
17
carica di un condensatore:
VR  VC  VB
R i 
q
 VB
C
R
VB
dq q
  VB
dt C
 t 

f (t )     1  e  



1
df (t )

   f (t )  
dt
t

 q(t )  VB  C  1  e RC 


t

dq(t ) VB
 i(t ) 

 e RC
R
dt
18
t

q(t )  VB  C  1  e RC 


q(t )  VB  C  e
  R C
t
Costante di tempo
RC
e 1  0.37
e x  a  x  ln a
(log b a  x  b x  a)
19
C=5nF
R=10kW
DV
t1 per q(t1)=0.5*q0 ?
q(t )  q0  e
q(t1 )  q0  e
t
t
1
RC
RC

 0.5  q0
e
t1
RC
 t1
 ln 0.5
R C
 0.5
 t1  R  C  ln 0.5  10  5 106 s  (0.69)  35 106 s
  R  C  10  5 10 s  50 10 s
6
6
20
Quando le ruote di un’auto rotolano sull’asfalto, elettroni si trasferiscono dal
terreno dei pneumatici e di qui alla corrozzeria.come se fosse
L’auto = un’armatura di condensatore e
terreno = armatura opposta
Quando si ferma, scarica, t=0.
V0=30 kV,
Capacita’ del condensatoire auto-suolo C=500 pF
Resitenza offerta da ciascun pneumatico Rpn=100GW.
Quanto tempo passa prima che l’energia immagazzinata E=50 mJ?
q
1
q2
q  dq 

C0
2C
 12  C  V 2  12  q  V
E  12  C V 2  12  500 pF  (30kV ) 2  225mJ
21
Quando si ferma, scarica, t=0. V0=30 kV,
Capacita’ del condensatoire auto-suolo C=500 pF
Resitenza offerta da ciascun pneumatico Rpn=100GW.
Quanto tempo passa prima che l’energia immagazzinata E=50 mJ?
q
1
q2
E   q  dq 
C0
2C
 12  C  V 2  12  q  V
E  12  C V 2  12  500 pF  (30kV ) 2  225mJ
1
4

 R  14 R pn  25 109 W
R R pn
  R  C  25GW  500 pF  12.5s
t
 2t
q0
q0
q(t ) 2
 2
E (t ) 

 (e ) 
e 
2C 2C
2C
E (t )
E (t  0)
q0 2t 
e
 2C
q0
2C
e
 2t


50mJ  2  t
50
 ln( )  t  9.4 s
75
225mJ 
22
Campi magnetici
Abbiamo visto dalla teoria di relatività: se un elettrone si muove rispetto a un filo nel quale
corre una corrente elettrica, il filo sembra carico per l’elettrone in movimento.
Questo effetto può essere calcolato con precisione e descrive in modo perfetto il
comportamento di una carica in moto.
23
Se invece si vuole evitare calcoli relativistici, si può in modo sperimentale esplorare la
forza che agisce su un elettrone in vicinanza di una corrente elettrica, e si può usare questa
forza per definire un così detto “campo magnetico”.
Si trova:

 
FB  q  v  B
FB  q  v  B  sin 
q

B

v
FB
Carica della particella
campo magnetico
velocità della particella
forza esercitata sulla particella
24


non
ha
mai
una
componente
parallela
a
v
FB
diverso da zero, perciò non può modificare la
velocità scalare
unità di misura:
1 tesla = 1 T = 1
N
N
N
1
1
C / s  m A  m
C  m / s 
25
Campo magnetico uniforme B, intensita 1.2 mT, orientato verticalmente verso l’alto.
Un protone con energia cinetica di 5.3 MeV si muove orizontalmente, da sud a
nord.
Quale forza di deflessione magentica agisce sul protone?
Trascurare il campo magnetico terrestre.
M(protone)= 1.67*10-27 kg, 1 MeV=1.60*10-13J

 
FB  q  v  B
da
Ecin 
1
2

m

v
2
2  Ecin
2  5.3MeV 1.60 1013 J / MeV
7
v


3
.
2

10
m/ s
 27
m
1.67 10 kg
FB  q  v  B  sin   1.60 1019 C  3.2 107 m / s 1.2 103 T  sin 900 
6.11015 N
Con accelerazione
FB
6.11015 N
12
2
a


3
.
7

10
m
/
s
m 1.67 1027 kg
26
Carica in moto circolare
Un corpo in moto circolare viene continuamente accelerato,
con una forza che punta verso il centro della circonferenza:
 

Dv  v  sin D   v  D
F  ma  m
dv
d
v
 mv
 m  v   m  v 
dt
dt
r
 
In un campo magnetico con B  v
v2
FB  q  v  B  m 
r
r
T 
mv
qB

Dv
D
D

v

v
v2
a
r
Accelerazione
centripeta
2
v
o F  m
forza centripeta
r
2   r 2  m  v 2  m




v
v qB
B q
Non dipende da v, ma solo di m/q =>
permette misura diretta di m/q
27
Forza magnetica agente su un filo percorso da
corrente
L
q  i  t  i  
 vd

 velocità di deriva vd

FB  q  vd  B  sin    i  L   vd  B  sin 900
vd 

 angolo compreso tra le direzioni di L e di B
FB  i  L  B

 
FB  i  L  B
28
Un filo rettilinieo orizzontale di rame e’percorso da un corrente i=28A.
Qual e’ l’intensita’e la direzione del campo magnetico B necessario a “far gallegiare”il
filo, cioe’ a bilanciare la suo forza di gravita’ Fg ?
La massa lineica (massa per unita’di lunghezza) del filo e’46.6 g/m.
FB  i  L  B  sin   m  g
m g
B

i  L  sin 
m L g 
i
46.6 10 3 (kg / m)  9.8m / s 2
 1.6 10  2 T
28 A
(circa 160 volte l’intensita’ del campo magnetico terrestre)
29
Momento torcente su una spira percorsa da corrente
Le due forze F e –F, che costituiscono una coppia di
forze, concordano nell’esercitare un momento della
forza complessiva sulla spira. Momento torcente
Il modulo ’ del momento torcente dovuto alla coppia di forze F1 e F2 e’:


b
2
 
 
b
2


    i  a  B   sin     i  a  B   sin    i  a  B  b  sin 
30
Se usiamo una serie di N spire, o avvolgimenti => bobina piana
  N    N  i  a  b  B  sin   N  i  A B  sin 
A  a  b
È la area racchiusa dalla bobina
La situazione può essere descritta in modo più sintetico, definendo
un dipolo magnetico
  N  i  A B  sin 

Direzione di
Barretta magnetica tipicamente
La terra
5J


 : quella del vettore n
T
8 1022 J
T
Un elettrone 9 1024 J
T
31
Visto che il campo magnetico non e’ altro che un campo elettrico “creato” da
un effetto relativistico, la sua forma dovrebbe essere quella del campo elettrico
– in quanto riguarda il modulo (dopo discutiamo la direzione)
Ci ricordiamo :
Se scegliamo come superficie una sfera con raggio r, e al centro la carica q,
otteniamo:
 
 0   E  dA   0  E   dA   0  E  4  r 2   q

1
q
E
 2
4    0 r

Legge di Coulomb
32
Simmetria cilindrica
r
(“carica uni-dimensionale”)
Una superficie gaussiana a forma di cilindro avvolge
una sezione di una lunghissima bacchetta cilindrica,
carica uniformemente (carica positiva)
Carica per lunghezza l
h

E
La carica racchiusa è:
 
 DA  E
 
  0   E  dA   0  E  2  r    h
l h
l
1
E

2  r   0 r
  0  E  2  r   h  l  h
33
Visto che il campo magnetico non e’ altro che un campo elettrico “creato” da
un effetto relativistico, la sua forma dovrebbe essere quella del campo elettrico
– in quanto riguarda il modulo (dopo discutiamo la direzione)
dq
dl
dq dq dl dq

 
 vd
dt dl dt dl
In corrispondenza:
Per un filo infinitamente lungo
0  4   107 T  m A
0  i
B
2   R
l
E
2  r   0
Permeabilità magnetica del vuoto
dq  vd
Per una “sorgente” infinitesimale
0 i  ds
dB 
 2
4  r
dq
E
1
4    0

q
r2
34

r
+

r

ds

B
dq
 
ds vd

E

 
B  const  r  ds
35
Per una “sorgente” infinitesimale
0 i  ds
dB 
 2  sin 
4  r
con  angolo fra ds e r
Legge di Biot-Savart
  0 i  ds  r
dB 

4 
r3
Per un filo infinitamente lungo:
0  i
B
2   R
0  4   107 T  m A
Permeabilità magnetica del vuoto
36
Regola della mano destra:
Afferrate l’elemento di filo nella mano
destra con il pollice puntato nel verso della
corrente.
La curvature delle altre dita indica il verso
delle linee del campo magnetico generato
da quell’elemento

 
 i  ds  r
dB  0 
4 
r3
37
Campo magnetico generato da una corrente in un filo piegato ad arco
Per il punto centro di curvatura:
0 i  ds  sin 900 0 i  ds
B


 2
2
4 
4  R
R


 i  R  d
0  i
0  i  
B   dB   0 


d


4 
4    R 0
4   R
R2
0
Per spira circolare:   2  
B
0  i
2 R
38
La figura presenta due lunghi fili paralleli percorsi dalle correnti i1 e i2 in
versi opposti. Che intensita’ e direzione ha il campo magnetico netto
generato nel punto P?
Si assumano i seguenti valori: i1=15 A, i2=32 A, d=5.3 cm
B1 
 0  i1
2   R
B2 
 0  i2
2   R
R  d  cos 450
B1 
0  i1
2    d  cos 450
B2 
0  i2
2    d  cos 450
39
Verso di B1, B2: regola della mano destra
B  B12  B22 
  arctan
0
2    d  cos 450
i12  i22 
B1
i
15 A
 arctan 1  arctan
 250
B2
i2
32 A
m
2
2
 15 A  32 A
4
A

1
.
89

10
T
2
0
2    5.3 10 m  cos 45
4   10 7 T
Vettore B forma con
asse x angolo di
  450  250  450  700
40
Forza tra due conduttori paralleli
B
0  i
2   R
campo magnetico prodotto dalla corrente nel filo a:
 Ba 
0  ia
2   d
Forza esercitata sulla lunghezza L del filo b:

 
Fba  ib  L  Ba
 
L  Ba
 Fba  ib  L  Ba 
0  L  ib  ia
2   d
Direzione:
Correnti parallele e concordi si attraggono e correnti parallele ma discordi si respingono
41
Legge di Ampere
Elettrostatica: legge di Gauss
Situazione analoga per
magnetismo:
 
 B  ds  0  ich
Si curvino le dita della mano destra attorno
alla linea chiusa nel verso di integrazione. A
una corrente passante nel verso indicato dal
pollice teso viene assegnato il segno piu’.
42
Per filo rettilineo infinito percorso da corrente:
 
 B  ds  B   ds  B  2  r    0  i
0  i
B
2  r 
Corrente i uscente dal piano della figura
43
solenoidi
44
  b
 B  ds   B  ds  B  h  0  i  n  h
a
 B  0  i  n
Solenoide ideale
n:= numero di spire per unita’ di
lunghezza del solenoide
45
Solenoide di lunghezza L=1.23 cm, diametro interno d=3.55 cm
Il solenoide sia composto da cinque strati di 850 spire l’uno e vi scorra una corrente
i=5.57 A.
Si calcoli il campo magnetico B nel centro del solenoide
B  0  i  n
 B  4   10 7 T
m
5  850 spire
 5.57 A 
 2.42 10  2 T
A
1.23m
46
V
R
i
C
q
V
B  L  i
Esempio: induttanza propria
di un solenoide rettilineo:
L=induttanza propria
L  0  n 2  A  l
n=spire all’unita’ di lunghezza
A*l=volume
47
Equazioni di Maxwell (1861-1864)
  1
 E  dS      dV
0
 
 B  dS  0
  d
  1
c   B  dr    E  dS 
dt
0
2
 
 j  dS
 
 
d
 E  dr   dt   B  dS
48