Ciclo Iterativo

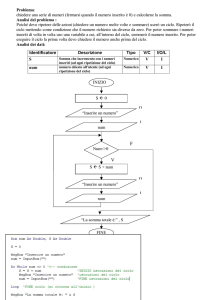
Cicli in Fortran
I cicli consentono di eseguire una sequenza di
istruzioni più di una volta
due tipi:
Cicli iterativi
Cicli while
Ciclo Iterativo
DO indice=inizio,fine,incremento
istruzione 1
istruzione 2
……………
blocco
END DO
indice è una variabile intera ed è utilizzatata
come contatore del ciclo
inizio, fine, incremento sono parametri
incremento è facoltativo se è omesso si assume
che è uguale a 1
Ciclo Iterativo
1) inizio, fine, incremento possono essere costanti,
variabili o espressioni;
se sono variabili o espressioni devono essere
valutate prima del ciclo
2) all’inizio del ciclo il programma pone indice=inizio
se indice*incremento =< fine*incremento
il programma esegue le istruzioni all’interno del ciclo
Ciclo Iterativo
3) eseguite le istruzioni all’interno del ciclo il
programma pone indice=indice+incremento
se indice*incremento =< fine*incremento
vengono eseguite nuovamente le istruzioni del ciclo
4) si ripete il punto 3) finchè
indice*incremento =< fine*incremento
quando questa condizione non è più vera viene
eseguita la prima istruzione dopo il ciclo
5) Si eseguono
n.iter.= (fine-inizio+incremento)/incremento
Ciclo Iterativo (esempi)
DO i=1,10,2
istruzione
……………
5 iterazioni
END DO
DO i=3,-3,-2
istruzione
……………
END DO
4 iterazioni
Istruzione CYCLE
Istruzione CYCLE interrompe l’esecuzione delle
istruzioni del ciclo e fa ritornare all’inizio del ciclo
L’indice del ciclo viene incrementato e l’esecuzione
delle istruzioni del ciclo riprende se l’indice non ha
raggiunto il suo valore
Istruzione CYCLE (esempio)
PROBLEM esempio
INTEGER :: I
DO i=1,10
IF ( i == 3 ) CYCLE
WRITE(*,*) i
END DO
END PROGRAM esempio
Si stampano tutti i numeri interi compresi tra 1 e 10
Escluso il numero 3
Istruzione EXIT
Istruzione EXIT interrompe l’esecuzione delle
istruzioni del ciclo, fa uscire dal ciclo
Viene eseguita la prima istruzione dopo END DO
del ciclo
Istruzione EXIT (esempio)
PROBLEM esempio
INTEGER :: I
DO i=1,10
IF ( i == 3 ) EXIT
WRITE(*,*) i
END DO
END PROGRAM esempio
Si stampa solamente il numero 1
Ciclo while
DO WHILE (espressione logica)
istruzione 1
istruzione 2
……………
blocco
END DO
quando l’espressione logica è .TRUE. il blocco
delle istruzioni del ciclo vengono ripetute
quando l’espressione logica è .FALSE. viene
eseguita la prima istruzione dopo END DO
Ciclo while
DO
…………...
IF (espressione logica) EXIT
……………
blocco
END DO
quando l’espressione logica è .TRUE. il blocco
delle istruzioni del ciclo vengono ripetute
quando l’espressione logica è .FALSE. viene
eseguita la prima istruzione dopo END DO
Ciclo while
PROBLEM esempio
DOUBLE PRECISION :: var,eps
eps=1.D0
DO
var=1.D0+eps
IF ( var.EQ.1.D0) EXIT
eps=eps/2.d0
END DO
WRITE(*,*) ‘ eps =’, eps
END PROGRAM esempio
Cicli DO con nome
[nome] DO indice = inizio, fine, incremento
…………...
…………...
IF (espressione logica) CYCLE [nome]
……………
……………
END DO [nome]
Cicli DO con nome
[nome] DO
…………...
IF (espressione logica) CYCLE [nome]
……………
…………...
IF (espressione logica) EXIT [nome]
……………
END DO [nome]
SUBROUTINE
SUBROUTINE nome_subr ( lista_argomenti )
sezione dichiarativa
sezione esecutiva
RETURN
END SUBROUTINE nome_subr
SUBROUTINE
PROGRAM nome_prog
CALL nome_subr ( lista_argomenti )
END PROGRAM nome_prog
SUBROUTINE
1) ogni subroutine è compilata separatamente dal
programma principale e da altre subroutine
quindi può usare le stessi nomi delle variabili e
le stesse etichette utilizzate dal programma
principale o da altre subroutine
2) l’ordine e il tipo degli argomenti della chiamata
devono corrispondere a quelli della definizione
SUBROUTINE
PROGRAM main
INTEGER, PARAMETER :: n=2
DOUBLE PRECISION :: f,x(n)
CALL funct( n,x,f )
END PROGRAM main
SUBROUTINE funct(n,x,f )
INTEGER :: n
DOUBLE PRECISION :: f,x(n)
Istruzione INTENT
INTENT(IN) l’argomento è un dato di input
INTENT(OUT) l’argomento è un dato di output
INTENT(IN OUT) l’argomento è sia un dato di
input che di output
se l’istruzione INTENT è assente l’argomento è
sia un dato di input che di output
Istruzione INTENT
SUBROUTINE funct(n,x,f )
INTEGER, INTENT(IN) :: n
DOUBLE PRECISION, INTENT(IN) :: x(n)
DOUBLE PRECISION, INTENT(OUT) :: f
FUNCTION
FUNCTION nome_funct ( lista_argomenti )
sezione dichiarativa
sezione esecutiva
nome_funct=espressione
RETURN
END FUNCTION nome_funct
FUNCTION
PROGRAM nome_prog
var=nome_funct( lista_argomenti )
END PROGRAM nome_prog
Calcolo del gradiente approssimato
f x, y 
f x, y 
x

x
 lim
f x     f x 

 0
f x     f x   errapp ( )  errtronc
errapp ( )


 0,
 0
Calcolo del gradiente approssimato
f x, y 
f x, y 
x

x
 lim
f x     f x 

 0
f x     f x   errapp ( )  errtronc
errapp ( )


 0,
 0
Calcolo del gradiente approssimato
per valori di

sufficientemente piccoli
f x, y 
x
f x, y 
f x, y 
x
x



f x     f x 

f x   f x   

f x     f x   
2
Forward formula
Backward formula
Symmetric formula
subroutine gradapp(n,x,f)
.................................
call funct(n,x,f)
do i=1,n
z=x
z(i)=x(i)+eps
call funct(n,z,fp)
g(i)=(fp-f)/eps
end do
return
end subroutine gradapp
Generatore di Numeri Pseudo-casuali
RANDOM_NUMBER(x)
x è un REAL
ritorna un valore estratto da una sequenza di numeri
pseudo-casuali
il valore restituito nella variabile x è compreso tra 0
(incluso) e 1 (escluso)
0  x 1
Gen. di Num. Cas. (esempio di numero in
PROGRAM num_cas
implicit none
real :: num
double precision, parameter :: l=-10, u=10
double precision :: dnum,x
call RANDOM_NUMBER(num)
dnum=dble(num)
x=l+dnum*(u-l)
stop
end program num_cas
[l,u) )
Sequenza pesudo-casuale
circa 1018 numeri
s
…
…
seed della sequenza
circa 1018 numeri
s
…
…
s
…
Inizializzazione della sequenza
RANDOM_SEED()
imposta l’innesco della sequenza random s ad un
valore ottenuto sulla base del tempo di sistema.
se CALL RANDOM_SEED() precede
l’istruzione CALL RANDOM_NUMBER(num)
ad ogni esecuzione del programma vengono
generati numeri differenti
altrimenti vengono generati gli stessi numeri