due

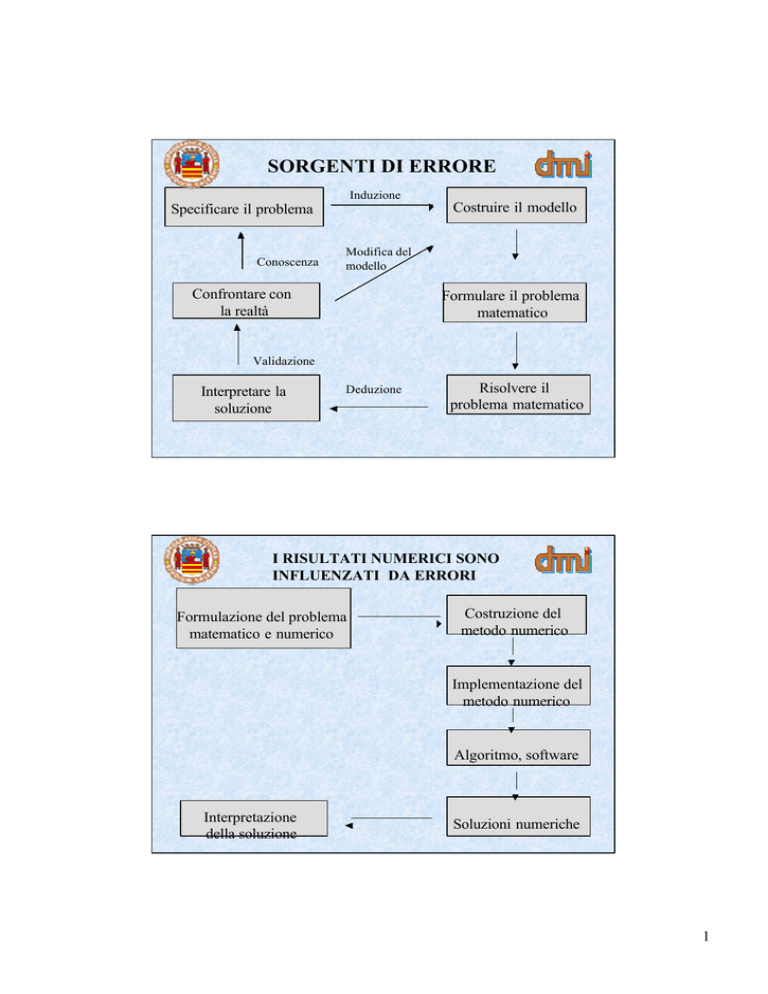
SORGENTI DI ERRORE
Induzione
Costruire il modello
Specificare il problema
Conoscenza
Modifica del
modello
Confrontare con
la realtà
Formulare il problema
matematico
Validazione
Interpretare la
soluzione
Deduzione
Risolvere il
problema matematico
I RISULTATI NUMERICI SONO
INFLUENZATI DA ERRORI
Formulazione del problema
matematico e numerico
Costruzione del
metodo numerico
Implementazione del
metodo numerico
Algoritmo, software
Interpretazione
della soluzione
Soluzioni numeriche
1
SORGENTI DI ERRORE
• Semplificazioni introdotte nel modello
Ad es., il modello è supposto lineare, oppure si
suppongono trascurabili alcune grandezze fisiche
(inadeguatezza del modello)
•Errori nei dati
errori di misurazione (sistematici e/o random)
•Errori di troncamento
Si introducono quando un procedimento infinito è
approssimato mediante procedimento finito: ad es.
derivata è approssimata con rapporto incrementale, etc.
•Errori di arrotondamento e troncamento nei dati e
•nei calcoli
Il nostro sistema di numerazione è posizionale.
N > 1 base
a = ±amam−1 ........
a1 a0 a−1 a−2 ........ 0≤ ai ≤ N−1 =
= ±am Nm + am−1 N m−1 + ......+ a1 N + a0 N 0 + a−1 N−1 + a−2 N−2 + .....
Ad ogni numero di macchina, rappresentato nella base del
calcolatore (2 o potenza di 2), è riservato uno spazio finito.
Interi:
Ad essi viene riservato un numero massimo fissato p di cifre.
Possono essere rappresentati solo gli n tali che
|n| < 2 p -1 (se la base del sistema di numerazione è 2).
Possibili errori:
•Gli n che non soddisfano la disuguaglianza non possono essere
rappresentati (errore di overflow).
•Il risultato di una divisione tra interi può non essere un intero.
Ad es. 8:4=2, ma
4:8=0, se si memorizza il risultato in una variabile intera
2
Errori nella rappresentazione dei
numeri reali
a ∈ ℜ, a = p N q
p reale, q intero (< = > 0), N base
p=mantissa, q=caratteristica.
Ogni numero reale si può rappresentare come coppia
(mantissa, caratteristica), fissata la base N del sistema di
numerazione.
Questa rappresentazione non è unica. Infatti
p
a = p N q = ( pN ) N q−1 = N q+1
N
Ad es.
123 = 123*100 =12,3*101 = 1,23*102 =
0,123*103 = 0,0123*104
La rappresentazione adottata sul calcolatore è
quella normalizzata, ovvero tale che
N −1 ≤ p <1
Nell’esempio precedente l’unica rappresentazione
normalizzata di 123 è 0,123*103. Le altre
rappresentazioni hanno una mantissa in modulo > 1,
oppure < 0.1 (l’ultimo caso).
Ai numeri reali è riservato un numero fissato di bits, t
bits per la mantissa, r bits per la caratteristica.
Di solito
t=6 in precisione semplice,
t=14 in doppia precisione.
r soddisfa m <= q <= M, con m, M che dipendono dal
calcolatore.
3
L’insieme dei numeri di macchina A⊂ ℜ è definito da r e t.
Se il numero di bits a disposizione della caratteristica (indicato con
r) non è sufficiente, il numero non può essere memorizzato
(overflow o underflow).
I numeri reali la cui mantissa, in forma normalizzata, necessitano di
un numero di bits > t, devono essere accorciati, ovvero la mantissa
viene accorciata per troncamento o arrotondamento.
Se x è un numero reale non di macchina, esso viene rappresentato
dal numero di macchina ad esso più vicino, ovvero:
a ∈ ℜ − Α → a ∈ Α t. c . | a − a | ≤ | a − g | ∀ g ∈ Α
a = pΝq →a = pΝq
Troncamento:
| p − p | ≤ Ν −t ,
p = 0. p1 p2 ....p t pt +1 ..., p = 0. p1 p2 ....pt .
Arrotondamento:
1 −t
Ν
2
p = 0 . p 1 p 2 ..... p t
| p − p |≤
p = 0 . p 1 p 2 ..... p t + 10
se 0 ≤ p t + 1 ≤ 4 ,
−t
se p t + 1 ≥ 5
Errore nella rappresentazione di un numero
reale in virgola mobile
• Errore assoluto
x− x
Se l’errore assoluto è ≤ 1 Ν − k , si dice che x ha k decimali
2
corretti.
x−x
• Errore relativo
x
x=p Ν q numero reale,
x = p Ν q numero di macchina
1
| p − p | ≤   Ν −t ,
| x − x |≤
2
Errore relativo: | x |=| p Ν q | = | p | Ν q ≥ Ν−1 Ν q =Νq−1,
Errore assoluto:
 1  q −t
 Ν
2
1
1
≤ q−1
| x| Ν
x−x x −x  1  q−t 1− q  1 1−t
≤ q−1 ≤   Ν Ν =   Ν
x
Ν
2 
 2
 1  1 −t
 Ν
2
è la precisione di macchina = eps
4
Somme in virgola mobile (+* )
•Somma di numeri con uguale caratteristica:
si sommano le mantisse, e si arrotonda.
b1 = 0.2841*10−3 ,
b2 = 0.4212*10−3
b1 + b2 = 0.7053*10−3 = b1 +* b2
•Se la mantissa risultante non è in modulo < 1 oppure
> N-1, si normalizza e si arrotonda.
b1 = 0 . 2841 * 10 − 3 ,
b 2 = 0 . 8112 * 10 − 3
b1 + b 2 = 1 . 0953 * 10 − 3
b1 + * b 2 = 0 . 1095 * 10 − 2
Somme in virgola mobile (+* )
•Somma di numeri con diversa caratteristica:
si trasforma il numero con caratteristica minore in
modo tale da avere caratteristica uguale all’altro numero.
b1 = 0.2841*10−3 ,
b2 = 0.4813*10−2
b1 = 0.02841*10−2
b1 + b2 = 0.50971*10−2
b1 +* b2 = 0.5097*10−2
•Ecco che cosa può accadere:
b1 = 0.2841*10−3 ,
b2 = 0.1248 *10 −7
b2 = 0.00001248*10 −3
b1 + b2 = 0.28411248*10−3
b1 +* b2 = 0.2841*10 −3 = b1
5
Prodotto e divisione virgola mobile (**, :*)
•Si moltiplicano le mantisse, si sommano le
caratteristiche, si normalizza e si arrotonda.
b1 = 0.1248 * 10−3 ,
b2 = 0.3144* 105
b1 * b2 = 0.03923712 * 102
b1 ** b2 = 0.3924 * 101
•Nella divisione il dividendo viene rappresentato con
il doppio delle cifre.
b1 = 0.7814 * 102 ,
b2 = 0.3148 * 101
b1 :b2 = 2.48221092* 101
b1 :* b2 = 0.2482 * 102
•Può accadere che i risultati di un calcolo tra numeri
di macchina diano numeri non rappresentabili.
y = a ** b
Overflow:
a = p1 Ν 1 ,
q
y =a:* b,
b= p2 Ν 2 ,
q
q1 >0, q2 <0,
M
, q1 +q2 > M
2
q1 −q2 >M
q1, q2 >
•Le operazioni di macchina non godono delle usuali
proprietà tra numeri reali:
Non valgono in generale:
a+*(b+* c) ≠ (a+* b)+*c
•la proprietà associativa:
*
*
*
*
*
•la proprietà distributiva: a * ( b + c ) ≠ ( a * b ) + ( a * c )
(a **b) :*b ≠ a
•la legge di semplificazione:
eps
•Ancora:
a +* b = a se |b | <
|a|
Ν
6
Effetto smearing
Perdita di cifre amplificata da cancellazione
t=8
a = 0.23371258 * 10 − 4
b = 0.33678429 * 10 2
c = − 0.33677811 * 10 2
a + * ( b + * c ) = a + * 0.00000618 * 10 2 =
= a + * 0 .61800000 * 10 − 3 = 0.64137126 * 10 −3
( a + * b ) + * c = ( 0. 0000002337 1258 * 10 2 + * b ) + * c =
= 0.33678452 * 10 2 + * c = 0 .64100000 * 10 − 3
Il risultato esatto è
0.641371258 * 10 −3
Nel I caso l’errore risulta inferiore (poiché la somma tra numero
“grande” e numero “piccolo” è stata eseguita come ultima operazione.
Nel II caso sommando a e b, di ordine di grandezza diverso, si sono
perse subito delle cifre nell’arrotondamento, che quindi non hanno poi
contribuito al risultato.
Supponiamo la mantissa di 4 cifre.
t=4
1 +*
10. 000
∑a
k =1
k
,
a k = 10 −4 ∀ k
1 + a 1 = 0.1000 * 10 1 + 0.1000 * 10 − 3 =
*
= 0.1000 * 10 1 + 0.00001 * 101 =
= 0.1000 * 101 = 1
Pertanto
1 +*
10.000
∑a
k
=1
k =1
Se invece si calcola prima la sommatoria, e poi si aggiunge 1, si
ottiene 2, ovvero
10.000
∑
a k +* 1 = 2
k =1
Quindi non vale la proprietà associativa, e l’errore maggiore viene
commesso sommando subito numeri di ordine di grandezza diversi.
7
Cancellazione numerica
• Errore nella sottrazione di numeri quasi uguali
a = p1 Ν q , b = p 2 Ν q
Supponiamo che coincidano le prime 3 cifre di p1 e p2.
q−3
Quindi nella mantissa della differenza a − b = p Ν
Solo le prime t-3 cifre provengono da p 1 e p2,
Le altre 3 cifre non hanno significato.
a−b = 0.000xx x...x xx 10q = 0. xx x...x x hhh 10q−3
1442443
14243{
t −3
t
Es:
N = 10 , t = 6
3
p 1 = 0 . 147554326
,
p 1 = 0 . 147554
p 2 = 0 . 147251742
,
p 2 = 0 . 147252
p = p1 − p 2 = 0 .000302584
= 0 . 302584
p = p1 − p 2 = 0 . 302000
−3
* 10
* 10
−3
Esempio di cancellazione numerica
Esempio:
Le radici di
x 2 −2a x + ε = 0
x1 = a+ a 2 −ε ,
sono:
x2 = a− a2 −ε
Se | ε | << | a |, allora x 2 è differenza di due
numeri quasi uguali.
Si può evitare la cancellazione numerica ponendo:
x1 =a+sg(a) a2 −ε ,
x2 =a− a2 −ε =
(a− a2 −ε ) (a+ a2 −ε )
(a+ a2 −ε )
=
ε
x1
8
Algoritmo per la determinazione di eps
Proprietà della precisione di macchina:
eps è il più piccolo numero positivo che viene
“sentito” nella somma ad 1, ovvero
1 +* a = 1 ∀a ∈ M, 0< a < eps
1 +* eps> 1
begin
eps:=1
repeat
eps := eps/2
until 1+eps = 1
eps:= 2 * eps
end
Algoritmo per la determinazione del più
piccolo numero rappresentabile
La precisione di macchina non è lo zero della macchina.
Numeri minori di eps possono essere rappresentati, ma
non vengono “sentiti” nella somma ad 1, cioè vengono
trattati come se fossero uguali a zero.
begin
min:=1
repeat
min := min/10
until min=0
end
Il più piccolo numero rappresentabile è il penultimo della lista
9
In binario un numero reale non ammette necessariamente
una rappresentazione finita, anche se in base dieci ha una
rappresentazione finita.
Ad es. 0.1, 0.01, 0.001 necessitano di infinite cifre binarie
a =(.x
x
−1
x
−2
x
−3
−1
x
−2
........ x
−n
M
= a M 
= { a M } M 
=  { { a M } M } ,
0 .1 * 2 = 0 .2 → x
−1
0 .2 * 2 = 0 .4 → x
−2
=0
0 .4 * 2 = 0 .8 → x
−3
=0
0 .8 * 2 = 1 .6 → x
−4
=1
0 . 6 * 2 = 1 .2 → x
−5
=1
0 .2 * 2 = 0 .4 → x
−6
=0
0 . 1 = 0 . 00011
{ x}= x − x 
=0
0011 0011 ........
0 .3 * 2 = 0 .6 → x
0.3
.... )
=0
−1
0 .6 * 2 = 1 . 2 → x
−2
=1
0 .2 * 2 = 0 . 4 → x
−3
=0
0 .4 * 2 = 0 . 8 → x
−4
=0
0 .8 * 2 = 1 . 6 → x
−5
=1
0 .6 * 2 = 1 . 2 → x
−6
=1
( 0 . 3 ) 10 = 0 . 01001 1001 .... = ( 0 . 01001 ) 2
0 . 25 * 2 = 0 . 50 → x
0.25
0 .5 * 2 = 1 .0 → x
−2
−1
=0
=1
( 0 . 25 ) 10 = ( 0 . 01 ) 2
10
Errori dovuti ad un cattivo calcolo numerico
http://www.math.psu.edu/dna/disasters
http://www.ima.umn.edu/~arnold/index.html
http://www.resonancepub.com/oops.htm
•Fallimento del Missile Patriot in Dharan, Saudi Arabia, il 25
Febbraio 1991: 28 morti. Attribuito ad uno scarso
trattamento degli errori d’arrotondamento.
•Esplosione immediatamento dopo la partenza del razzo
Ariane 5 lanciato dall’Agenzia Spaziale Europea nella Guiana
Francese, il 4 Giugno 1996. Conseguenza di un semplice
overflow.
•Affondamento della piattaforma Sleipner A per la produzione
di petrolio e gas in Gandsfjorden near Stavanger, Norvegia, il
23 Agosto 1991. Causata da un’analisi inaccurata mediante
elementi finiti.
11