Di Parola Umberto e Pani Lara
Aritmetica di
macchina
Operazioni di macchina
Numeri di macchina
Numeri di macchina
?
Spazio limitato sul calcolatore
Rappresentazione in virgola
mobile o Floating-point
Approssimazione
Errore assoluto (Ea) |(x - x°)|
Errore relativo (Er) |(x - x°)/x|
Precisione di macchina o ε di
macchina (eps)
Data una mantissa di t cifre, l’approssimazione può avvenire per
Troncamento
Arrotondamento
• Escludo la parte destra della
t-esima cifra
• Errore relativo elevato
• Errore assoluto: |x - x°| < β-t
• eps=N1-t
• Aggiungo ½ N-t alla
mantissa in questione e poi
tronco quest’ultima alla tesima cifra
• Errore relativo basso
• Errore assoluto: |x - x°| < ½
β-t
• eps= ½ N1-t
t=6
1,2659298 1,26592
Er = (1,2659298 - 1,26592)/1,2659298
= 7,74 *10-6
1,2659298 1,26593
Er = (1,2659298 - 1,26593)/1,2659298
= -1,58*10-8
le operazioni di macchina (funzionali all’applicazione di operazioni
aritmetiche ai numeri macchina), che a due numeri macchina ne
associano un terzo, ottenuto arrotondando (attraverso le tecniche
precedentemente viste) l’esatto risultato dell’operazione aritmetica in
questione.
eps, |ε| ≤ eps
Sia ε l’errore relativo
della rappresentazione
di x (ε = (fl(x) – x)/x ⇒
fl(x) = x (1 + ε))
fl(x)
l’operazione
di
approssimazione di x a
numero di macchina in
aritmetica floating-point
fl(x) = x(1 + ε), |ε| ≤ eps
a ⊕ b = fl(fl(a) + fl(b)) = (fl(a) + fl(b))(1 +ε1), |ε1| ≤ eps;
a ---- b = fl(fl(a) − fl(b)) = (fl(a) − fl(b))(1 +ε2), |ε2| ≤ eps;
a ⊗ b = fl(fl(a) × fl(b)) = (fl(a) × fl(b))(1 +ε3), |ε3| ≤ eps;
a // b = fl(fl(a) / fl(b)) = (fl(a) / fl(b))(1 +ε4), |ε4| ≤ eps.
• Principio di equivalenza:
si definiscono equivalenti due espressioni che in aritmetica
finita forniscono risultati la cui distanza relativa differisce
di una quantità dell’ordine della precisione di macchina.
• Proprietà
• Rappresentazione in linguaggio Java
• Overflow e underflow
Propietà
Non tutte le proprietà delle operazioni aritmetiche si
conservano per le operazioni di macchina.
La proprietà commutativa per somma e prodotto si
conserva anche per le operazioni di macchina:
a ⊕ b = b ⊕ a, a ⊗ b = b ⊗ a,
Ma non valgono più le seguenti proprietà:
• a ⊕ (b ⊕ c) ≠ (a ⊕ b) ⊕ c,
• a ⊗ (b ⊗ c) ≠ (a ⊗ b) ⊗ c,
• a ⊗ (b ⊕ c) ≠ (a ⊗ b) ⊕ (a ⊗ c),
• (a ⊗ b) // b ≠ a,
• (a // b) ⊗ b ≠ a,
• (a ⊗ b) // c ≠ (a // c) ⊗ b.
Rappresentazione in Java
Overflow e Underflow
elaborazione eccedente, per numero di cifre rispettivamente
positive e negative, il limite della capacità di una memoria.
ERRORE
Errore
Cancellazione numerica: Si dice cancellazione numerica il
fenomeno di perdita di cifre significative che si verifica quando
si opera una sottrazione tra due numeri di macchina “quasi
uguali” tra loro (ovvero, il risultato è più piccolo di ciascuno dei
due operandi). TUTTAVIA, la sottrazione non genera problemi
in sé, ma amplifica errori di approssimazione già esistenti sugli
operandi.
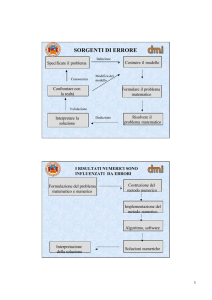
Applicazione di algoritmi: Valutando l’algoritmo nella sua
stabilità numerica e nella qualità del condizionamento del
problema rispetto a cui è applicato, si giunge ad ipotizzare
l’incidenza di tre tipi di errori.
Più nello specifico, considerando un generico problema di
partenza descritto da una funzione esplicita y = f(x), si ha…
fl(x1) = 0.191019 · 103 , fl(x2) = 0.191017 · 103
fl(x1) ----- fl(x2) = 0.000002 · 103 = 0.200000 · 10-2
fl(x1) = 0.191020 · 103 , fl(x2) = 0.191017 · 103
fl(x1) ----- fl(x2) = 0.000003 · 103 = 0.300000 · 10-2
[|(fl(x1) ----- fl(x2)) − (x1 − x2)| ]/ [|(x1 − x2)|] = 0.1363
Nel campo pratico tali forme di errore possono essere, in certi casi,
parzialmente ridotte (ma non evitate) tramite il ricorso a formulazioni
alternative, dove il fenomeno della cancellazione numerica si riduce di
entità:
Esempio 1: Le radici di un equazione di secondo grado (x2
- 2ax + ε = 0) si trasformano ne seguente modo, al fine di
evitare l’applicazione della sottrazione, che produce un
maggiore errore (obbiettivo condiviso anche con i successivi
esempi): x1= a + √a2 - ε e x2 = a - √a2 - ε = ε/x1.
Esempio 2: √x + ε - √ε = ε/(√x + ε + √x).
Esempio 3: cos(x+ε) – cos(x) = -2sin(ε/2) sin(x + ε/2).
• un errore x - x°, al quale corrisponde un errore finale,
dovuto non all’algoritmo, ma unicamente alla funzione f(x)
(condizionamento): e1 = f(x) – f(x°).
• Un errore derivante dal fatto che spesso f viene
approssimata con una funzione più semplice f1 (algoritmo);
in questo caso abbiamo un ulteriore errore, detto di
troncamento o discretizzazione: e2 = f(x°) – f1 (x°).
• Infine, le operazioni eseguite dal calcolatore nella
valutazione di f1(x°) non sono esatte: invece del valore f1(x°)
otterremo un valore f2(x°). L’errore: e3= f1 (x°) – f2(x°) , è
dovuto alla propagazione degli errori di arrotondamento
nel calcolo numerico f1(x°), di cui è responsabile la stabilità
numerica dell’algoritmo.
Ecco come si riscontra l’errore in Java
(terzo caso)
Bibliografia
• “100 pagine di elementi di calcolo numerico” di
G.Monegato;
• “Informatica 3 quinto anno licei scientifici opzione
scienze applicate” di Piero Gallo e Pasquale Sirsi;
Sitografia
• https://www.youtube.com/ (nella stesura de “video”);
• http://www.dm.uniba.it/~delbuono/floating_eliaiavernaro.
pdf;
• http://calvino.polito.it/~sberrone/Faculty/01ILRFW.2011/
1_RappresentazioneNumeri.pdf;