Punto nave con rilevamento polare 45° e Traverso
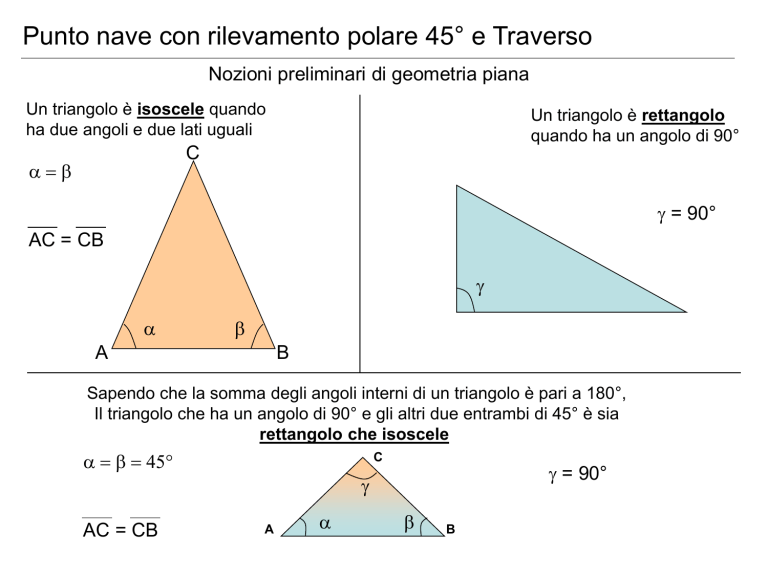
Nozioni preliminari di geometria piana
Un triangolo è isoscele quando
ha due angoli e due lati uguali
Un triangolo è rettangolo
quando ha un angolo di 90°
C
=b
g = 90°
AC = CB
g
b
A
B
Sapendo che la somma degli angoli interni di un triangolo è pari a 180°,
Il triangolo che ha un angolo di 90° e gli altri due entrambi di 45° è sia
rettangolo che isoscele
= b = 45
C
g = 90°
g
AC = CB
A
b
B
Punto nave con rilevamento polare 45° e Traverso
Perché il punto nave sia attendibile si devono verificare due condizioni:
• Assenza della corrente
• Prora vera e Velocità propria costanti
Spiegazione per assurdo
1.
Immaginiamo di sapere la nostra posizione
2.
Sappiamo anche la Pv e la Vp (es. 090° - 9kts)
3.
Nel punto “A”, alle 1030 la nave rileva il faro 45° a sinistra
dalla prora (rSN = 45°)
4.
Quando la nave passa al traverso del faro (rSN = 90°) sono le
1050 (punto “B”)
5.
La nave in 20 minuti, alla velocità di 9 nodi, ha percorso 3 Nm
C
90°sn
45°sn
A
10.30
B
3 Nm
10.50
Punto nave con rilevamento polare 45° e Traverso
Perché il punto nave sia attendibile si devono verificare due condizioni:
• Assenza della corrente
• Prora vera e Velocità propria costanti
Spiegazione per assurdo
Consideriamo adesso il triangolo ABC
7
Ha un angolo di 45° (primo rilevamento) uno di 90° (supplementare al secondo rilevamento) ed il terzo (quello in corrispondenza del faro) risulta anch’esso essere di 45° (perché 180°- 45°90° = 45°)
8
Se gli angoli sono i suddetti allora il triangolo è rettangolo ma
soprattutto isoscele.
9
Quindi il lato AB è uguale al lato BC.
10
Questo significa che il faro dista 3 miglia dal punto in cui io lo
vedo al traverso (la stessa distanza che ho percorso tra A e B).
C
45°
3 Nm
6
90°sn
45°sn
A
10.30
B
3 Nm
10.50
Punto nave con rilevamento polare 45° e Traverso
Perché il punto nave sia attendibile si devono verificare due condizioni:
• Assenza della corrente
• Prora vera e Velocità propria costanti
Cosa avviene nella realtà
1.
Vedo il bersaglio 45° a sinistra della mia prora, NON
DISEGNO NIENTE, ma prendo il “VIA AL TEMPO” e comincio
a contare il tempo, SENZA CAMBIARE ROTTA e VELOCITA’
2.
Arrivo sul traverso sinistro del faro, do lo “STOP AL TEMPO” e
disegno il rilevamento vero del faro (Rlv = Pv – rSN). In
questo caso Rlv = Nord.
3.
Sono passati 20 minuti
4.
In venti minuti calcolo di avere fatto 3 miglia (SPAZIO =
VELOCITA’ * TEMPO) spazio = 9 * 0,3333333 = 3Nm
5.
Per la spiegazione della lastrina precedente (triangolo
rettangolo isoscele) vuol dire che la distanza tra me e il faro al
momento del traverso era 3 Nm.
6.
Traccio l’arco di cerchio di raggio 3 Nm dal faro che interseca
il rilevamento e TROVO IL PUNTO NAVE DELLE 1050!
10.50