Lezione 8

Forza di Lorentz
ago della bussola
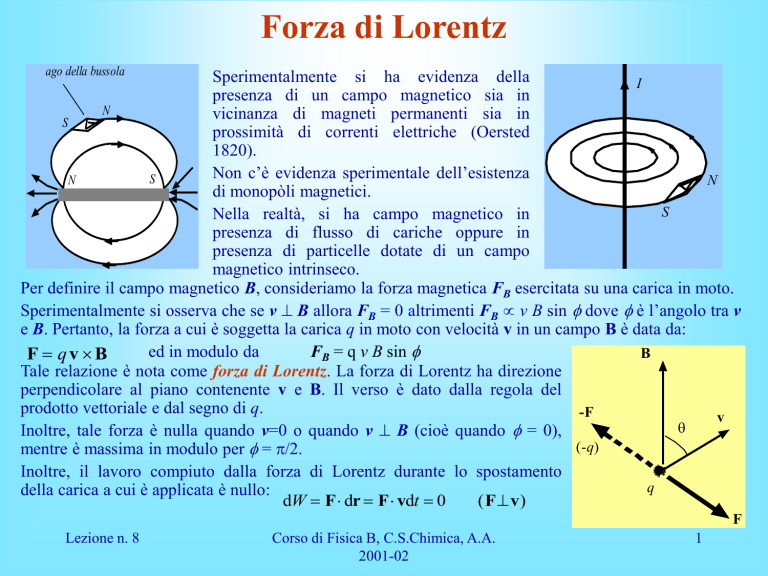
Sperimentalmente si ha evidenza della
I
presenza di un campo magnetico sia in
N
vicinanza di magneti permanenti sia in
S
prossimità di correnti elettriche (Oersted
1820).
Non c’è evidenza sperimentale dell’esistenza
S
N
N
di monopòli magnetici.
S
Nella realtà, si ha campo magnetico in
presenza di flusso di cariche oppure in
presenza di particelle dotate di un campo
magnetico intrinseco.
Per definire il campo magnetico B, consideriamo la forza magnetica FB esercitata su una carica in moto.
Sperimentalmente si osserva che se v  B allora FB = 0 altrimenti FB  v B sin f dove f è l’angolo tra v
e B. Pertanto, la forza a cui è soggetta la carica q in moto con velocità v in un campo B è data da:
ed in modulo da
FB = q v B sin f
B
F  qv B
Tale relazione è nota come forza di Lorentz. La forza di Lorentz ha direzione
perpendicolare al piano contenente v e B. Il verso è dato dalla regola del
prodotto vettoriale e dal segno di q.
-F
v

Inoltre, tale forza è nulla quando v=0 o quando v  B (cioè quando f = 0),
(-q)
mentre è massima in modulo per f = p/2.
Inoltre, il lavoro compiuto dalla forza di Lorentz durante lo spostamento
q
della carica a cui è applicata è nullo:
dW  F dr  F vdt  0
(Fv)
F
Lezione n. 8
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
1
Forza magnetica agente su una particella
Tale relazione è nota come forza di Lorentz. La forza di Lorentz ha direzione perpendicolare al piano contenente
v e B. Il verso è dato dalla regola del prodotto vettoriale e dal segno di q.
Qui
il
campo
magnetico è uscente
dal
piano
della
pagina
Inoltre, tale forza è nulla quando v=0 o quando v  B (cioè quando f = 0), mentre è massima in modulo per f =
p/2.
Inoltre, il lavoro compiuto dalla forza di Lorentz durante lo spostamento della carica a cui è applicata è nullo:
dW  F dr  F vdt  0
(Fv)
Ciò ha come conseguenza che la forza di Lorentz non può modificare l’energia cinetica di una particella (non
compie lavoro!) ma può però modificarne la traiettoria.
In presenza di campo elettrico e magnetico contemporaneamente la forza di Lorentz può essere generalizzata
come:
F  q E  v  B
Lezione n. 8
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
2
Linee di campo magnetico
Il campo magnetico B può essere rappresentato con linee di forza alle quali è
tangente in ogni punto e la densità delle quali è proporzionale all’intensità di B.
A differenza del campo elettrico, le linee di campo magnetico sono linee chiuse ed
entrano dentro il magnete. Il campo è più intenso vicino alle estremità del magnete
(come confermano gli esperimenti).
Il polo magnetico da cui emergono le linee di campo è detto polo nord, l’altro polo
sud. Poli magnetici opposti si attraggono, poli magnetici simili si respingono.
Lezione n. 8
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
3
Scoperta dell’elettrone
Quando B ed E hanno direzioni perpendicolari tra loro, si dicono campi incrociati.
Nel 1897 J. J. Thomson (Università di Cambridge) scoprì l’elettrone usando un tubo a raggi catodici
(schermo TV). In tale dispositivo, all’interno delle piastre del condensatore è presente sia un campo
elettrico diretto dall’alto verso il basso, sia un campo magnetico ortogonale alla pagina ed entrante in
essa.
Regolando opportunamente il campo elettrico E è possibile imprimere una deviazione al fascio di
elettroni, dovuta al fatto che tra le piastre il moto è parabolico. L’altezza raggiunta dalla particella
sullo schermo vale:
v=velocità della particella
m=massa della particella
qEL2 L=lunghezza dei piatti
y
q=carica della particella
2mv2 E=campo elettrico
Regolando poi opportunamente il campo magnetico B, è possibile annullare l’effetto dovuto ad E:
quando le due forze si bilanciano si ha q E = q v B cioè v = E / B
da cui si ottiene:
m B 2 L2

q
2 yE
Lezione n. 8
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
4
Effetto Hall
Nel 1879 E. H. Hall dimostrò che anche gli elettroni di conduzione (e
qualunque portatore di carica in moto) risente degli effetti dovuti alla
forza di Lorentz.
In figura è riportata una lamina di Cu di larghezza d nella quale scorre una
corrente i dall’alto verso il basso. I portatori di carica (elettroni) si
muovono pertanto con velocità diretta dal basso verso l’alto (vd).
Se si applica un campo magnetico esterno B perpendicolare al piano, ogni
elettrone è soggetto alla forza di Lorentz FB diretta da sinistra verso
destra. Gli elettroni si ammasseranno quindi verso destra generando un
campo elettrico longitudinale E, diretto da sinistra verso destra. E avrà
come effetto quello di generare una forza elettrica FE diretta da destra
verso sinistra che si opporrà a FB. La situazione all’equilibrio sarà quella
per cui FE = - FB e quindi gli elettroni si muoveranno rettilineamente. Ma
sarà presente una d.d.p. tra il lato destro ed il lato sinistro della lastra, dato
da V = E d
Evidentemente, quando sono gli elettroni a muoversi, il lato sinistro avrà
potenziale positivo, mentre se i portatori di carica sono positivi (es.
semiconduttori) il lato destro avrà potenziale positivo.
L’uguaglianza delle forze implica e E = e vd B
da cui, sostituendo
vd,
vd 
j
i

ne neA
Lezione n. 8
si ha:
n
Bi
Vle
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
5
Cariche in moto circolare
Quando una carica entra in una zona con campo magnetico ortogonale alla sua
velocità iniziale v, essa è soggetta alla forza di Lorentz che a sua volta è
ortogonale a v. Per quanto si è visto, il modulo di v rimane costante (la forza di
Lorentz non compie lavoro) e quindi anche l’energia cinetica non varia:
S
q
+
K
B
v
N
1
m v 2  costante
2
F v
In tutti i casi in cui la forza è ortogonale alla velocità e l’energia cinetica si
conserva, si ha moto circolare uniforme (a = accelerazione centripeta = v2/r)
mv
m v2
si può ricavare il raggio dell’orbita: R 
qv B 
qB
R
2p R 2p m
q
B
Il periodo vale T 
, la frequenza f 
e la vel. angolare  c  q B

v
2p m
qB
m
v
Si noti che frequenza e velocità
angolare sono indipendenti da v, e
dipendono solo dal rapporto q/m. Il
raggio invece ha un segno
dipendente dal valore di q, per cui
guardando il verso di rotazione si
deduce la carica q.
Lezione n. 8
+
q
•
•
•
B
v
•
•
•
•
•
•
+
q
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
6
Traiettorie elicoidali
Se la velocità della particella carica non è
perpendicolare a B la particella sarà soggetta ad
un moto rettilineo uniforme nella direzione di B ed
ad un moto circolare uniforme nella direzione ad
esso perpendicolare, per cui il moto risultante sarà
elicoidale.
Se il campo magnetico B non è omogeneo, la
particella sarà soggetta ad un moto a spirale con
raggio variabile.
Se le disuniformità di B sono molto forti, la
particella può rimanere imbottigliata nel campo
magnetico ed essere riflessa avanti ed indietro.
Un tale fenomeno si verifica nell’alta atmosfera
terrestre, in prossimità dei poli, nelle fasce di Van
Allen. L’addensarsi degli elettroni produce un
campo magnetico che talora dà origine alle aurore
polari.
Lezione n. 8
B

y
v
+
q
x
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
7
Strumenti
Gli spettrometri di massa misurano la massa degli ioni. Lo ione carico q, inizialmente fermo, viene
accelerato da un campo elettrico fino a penetrare nella zona interessata dal campo magnetico, dove è
soggetto ad una traiettoria circolare con raggio x = 2 R che, come si è visto, dipende da m / q.
I ciclotroni sono dispositivi per accelerare le particelle costituiti da due semidischi a forma di D nei
quali è presente un campo magnetico ortogonale al piano della figura e tra i quali è presente un
campo elettrico che cambia segno ad ogni semirotazione delle particelle (che, come si è visto, hanno
periodo di rotazione indipendente dal raggio dell’orbita). In questo modo, ad ogni passaggio tra le
due D l’energia cinetica della particella aumenta e quindi il raggio R = m v / q B dell’orbita aumenta.
Lezione n. 8
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
8
Forza magnetica agente su un filo percorso da corrente
Un filo verticale in cui circoli una corrente è soggetto ad una forza in quanto tutti i portatori di carica
all’interno del filo, in moto con velocità vd, sono soggetti alla forza di Lorentz. Nel tempo t tutti i
portatori di carica compresi nel tratto L trasportano la carica q = i t = i L / vd attraverso una sezione
del filo. La forza di Lorentz può essere scritta quindi come FB = q vd B sin 90° = i L B
Se il campo magnetico B non è perpendicolare al filo, si avrà F  I l  B
mentre se il filo non è
rettilineo si avrà l’espressione:
F  I dl B

l
B
I dl
dl
F
Unità di misura di B nel sistema SI
tesla (T = N A-1 m-1)
Lezione n. 8
Osservazioni
all’elemento di corrente è applicata una forza (forza
magnetica) perpendicolare a I dl.
Vi è un’unica direzione per cui all’elemento di
corrente non è applicata alcuna forza: è la direzione di
B.
La forza è perpendicolare alla direzione di dl e alla
direzione di B.
L’intensità della forza è proporzionale alla lunghezza
dell’elemento di corrente, all’intensità della corrente I
e a sin ( = angolo tra il vettore I dl e il vettore B):
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
9
Momento torcente
Consideriamo una spira in un
campo magnetico uniforme B.
Ogni lato della spira quadrata è
soggetto alla forza magnetica.
F2 = i b B sin (90°-) = i b B cos 
Anche la forza sul lato 4 vale:
F4 = i b B sin (90°-) = i b B cos 
ma è diretta nel verso opposto.
Per le altre due si ha:
F1 = F3 = i a B
e costituiscono una coppia di forze.
che provoca la rotazione della spira. Il momento meccanico vale:
Cioè, sostituendo:
t  Fb sin 
t  I B a b sin   I ABsin 
Definendo il momento magnetico della spira come m = I A, si può scrivere
t = m B sin 
Oppure, in forma vettoriale,
t = mB
Questi fenomeni sono utilizzati nei galvanometri, misuratori di corrente molto
sensibili che funzionano appunto misurando il momento torcente agente su una
serie di spire.
Lezione n. 8
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
10
Momento di dipolo magnetico
Da quanto si è visto, l’equazione t = m  B definisce
il momento torcente agente su una spira percorsa da
corrente mediante il vettore m = i A momento di
dipolo magnetico.
Nel caso più generale di una bobina con N spire, si
scriverà m = N i A dove il verso di m è come indicato
in figura (regola della mano destra).
Il dipolo magnetico deve allora possedere un’energia
potenziale magnetica che dipende dall’orientamento del dipolo nel campo. Essa vale:
U = - m  B
Ed è minima quando il dipolo è allineato con il campo magnetico, e massima quando è
antiallineato. In caso di rotazione del dipolo magnetico, il lavoro compiuto sul dipolo dal
campo magnetico vale:
L = - DU = - ( Uf – Ui)
E per ruotare il dipolo di un certo angolo:
W

 mBsin  d  mBcos
0
Lezione n. 8
0
 cos 
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
11