Le quattro operazioni

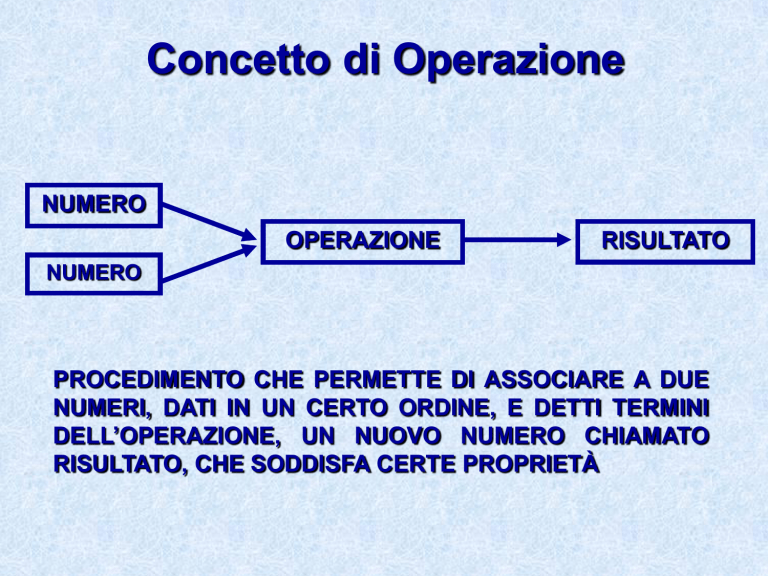
Concetto di Operazione
NUMERO
OPERAZIONE
RISULTATO
NUMERO
PROCEDIMENTO CHE PERMETTE DI ASSOCIARE A DUE
NUMERI, DATI IN UN CERTO ORDINE, E DETTI TERMINI
DELL’OPERAZIONE, UN NUOVO NUMERO CHIAMATO
RISULTATO, CHE SODDISFA CERTE PROPRIETÀ
Addizione in N
SEGNO DI
OPERAZIONE
5 + 3 = 8
ADDENDI
SOMMA O
TOTALE
L’ADDIZIONE È L’OPERAZIONE ARITMETICA CHE ASSOCIA A DUE
NUMERI DETTI ADDENDI UN TERZO NUMERO DETTO SOMMA CHE SI
OTTIENE CONTANDO DOPO IL PRIMO NUMERO TANTE UNITA’
QUANTE SONO QUELLE INDICATE DAL SECONDO
Proprietà dell’Addizione
PROPRIETÀ COMMUTATIVA
La somma di due o più numeri non cambia “scambiando”
l’ordine degli addendi:
8 + 3 = 11
3 + 8 = 11
8+3=3+8
PROPRIETÀ ASSOCIATIVA
La somma di due o più numeri non cambia se al posto di alcuni
addendi si sostituisce la loro somma:
4 + 2 + 3 = (4 + 2) + 3 = 6 + 3 = 9
4 + 2 + 3 = 4 + (2 + 3) = 4 + 5 = 9
PROPRIETÀ DISSOCIATIVA
La somma di due o più numeri non cambia se a uno o più
addendi se ne sostituiscono altri aventi per somma l’addendo
considerato:
9 + 6 = 15
(2 + 7) + 6 = 2 + 7 + 6 = 15
9 + (2 + 4) = 9 + 2 + 4 = 15
ELEMENTO NEUTRO
Lo zero è l’elemento neutro dell’addizione:
8+0=0+8=8
LEGGE DI COMPOSIZIONE INTERNA
L’addizione è una operazione interna all’insieme dei numeri naturali:
addizionando due numeri naturali si ottiene sempre un numero
naturale:
12 + 8 = 20
NUMERO
NATURALE
NUMERO
NATURALE
NUMERO
NATURALE
Sottrazione in N
SEGNO DI
OPERAZIONE
9 MINUENDO
4 = 5
SOTTRAENDO
DIFFERENZA
LA SOTTRAZIONE È L’OPERAZIONE ARITMETICA CHE
ASSOCIA A DUE NUMERI, DETTI MINUENDO E
SOTTRAENDO, DI CUI IL PRIMO MAGGIORE O UGUALE
AL SECONDO, UN TERZO NUMERO DETTO DIFFERENZA
CHE, ADDIZIONATO AL SECONDO NUMERO, DA’ PER
SOMMA IL PRIMO
Proprietà della Sottrazione
PROPRIETÀ INVARIANTIVA
La differenza fra due numeri non cambia se ad entrambi si
addiziona, o si sottrae se possibile, uno stesso numero:
8-5=3
(8 + 2) - (5 + 2) = 10 - 7 = 3
(8 - 3) - (5 - 3) = 5 - 2 = 3
LA SOTTRAZIONE E’ L’OPERAZIONE INVERSA DELL’ADDIZIONE
12 - 7 = 5
PERCHE’
7 + 5= 12
Moltiplicazione in N
SEGNO DI
OPERAZIONE
MOLTIPLICANDO
5 × 3 = 15
MOLTIPLICATORE
FATTORI
PRODOTTO
LA MOLTIPLICAZIONE È L’OPERAZIONE CHE ASSOCIA A DUE NUMERI
DETTI FATTORI UN TERZO NUMERO DETTO PRODOTTO CHE SI
OTTIENE ADDIZIONANDO TANTI ADDENDI UGUALI AL PRIMO
NUMERO QUANTI NE INDICA IL SECONDO
Proprietà della Moltiplicazione
PROPRIETÀ COMMUTATIVA
Il prodotto di due o più numeri non cambia cambiando
l’ordine dei fattori:
4 × 3 = 12
3 × 4 = 12
4×3=3×4
PROPRIETÀ ASSOCIATIVA
Il prodotto di due o più numeri non cambia se al posto di alcuni
addendi si sostituisce il loro prodotto:
2 × 3 × 4 = (2 × 3) × 4 = 6 × 4 = 24
2 × 3 × 4 = 2 × (3 × 4) = 2 × 12 = 24
PROPRIETA’ DISSOCIATIVA
Il prodotto di due o più numeri non cambia se a uno o più
fattori se ne sostituiscono altri aventi per prodotto il fattore
sostituito
12 × 6 = 72
(3 × 4) × 6 = 3 × 4 × 6 = 72
12 × (2 × 3) = 12 × 2 × 3 = 72
PROPRIETÀ DISTRIBUTIVA DELLA
MOLTIPLICAZIONE
RISPETTO ALL’ADDIZIONE
Per moltiplicare una somma per un numero, si può moltiplicare ogni
addendo della somma per quel numero e poi addizionare i prodotti
così ottenuti:
(2 + 4) × 5 = 6 × 5 = 30
(2 + 4) × 5 = 2 × 5 + 4 × 5 = 10 + 20= 30
PROPRIETÀ DISTRIBUTIVA DELLA
MOLTIPLICAZIONE
RISPETTO ALLA SOTTRAZIONE
Per moltiplicare una differenza per un numero, si può moltiplicare
ogni addendo della somma per quel numero e poi addizionare i
prodotti così ottenuti:
(10 - 4) × 3 = 6 × 3 = 18
(10 - 4) × 3 = 10 × 3 - 4 × 3 = 30 - 12= 18
ELEMENTO NEUTRO
L’uno è l’elemento neutro della moltiplicazione:
7×1=1×7=7
ELEMENTO ASSORBENTE
Lo zero è l’elemento assorbente della moltiplicazione, cioé annulla
sempre il prodotto:
5×0=0×5=0
e vale
0×0=0
LEGGE DI COMPOSIZIONE INTERNA
La moltiplicazione è una operazione interna all’insieme dei numeri
naturali: se moltiplico due numeri naturali ottengo sempre un
numero naturale
2 × 8 = 16
NUMERO
NATURALE
NUMERO
NATURALE
NUMERO
NATURALE
Divisione in N
DIVISIONE ESATTA O PROPRIA:
15 :
SEGNO DI
OPERAZIONE
3 = 5
DIVIDENDO
DIVISORE
QUOTO
LA DIVISIONE È L’OPERAZIONE ARITMETICA CHE ASSOCIA A
DUE NUMERI, DETTI DIVIDENDO E DIVISORE, DI CUI IL
SECONDO DIVERSO DA ZERO, UN TERZO NUMERO DETTO
QUOZIENTE CHE MOLTIPLICATO PER IL 2° NUMERO DA’ PER
RISULTATO IL 1°
LA DIVISIONE E’ L’OPERAZIONE INVERSA DELLA MOLTIPLICAZIONE
12 : 6 = 2
PERCHE’
6 x 2 = 12
Divisione in N
DIVISIONE APPROSSIMATA O IMPROPRIA:
SEGNO DI
OPERAZIONE
13 :
DIVIDENDO
3 = 4 e resto
DIVISORE 1 QUOZIENTE
RESTO
QUOZIENTE × DIVISORE + RESTO = DIVIDENDO
4 × 3 + 1 = 13
PROPRIETÀ INVARIANTIVA PER
LA DIVISIONE ESATTA
MOLTIPLICANDO O DIVIDENDO IL DIVISORE E IL
DIVIDENDO PER UNO STESSO NUMERO IL QUOZIENTE
NON CAMBIA:
12 : 6 = 2
(12 × 4) : (6 × 4) = 48 : 24 = 2
(12 : 3) : (6 : 3) = 4 : 2 = 2
Approfondimento sulla Divisione
quoziente di due numeri uguali:
12 : 12 = 1
Se il divisore è uguale a 1 il quoziente è uguale al dividendo:
12 : 1 = 12
Se il dividendo è uguale a 0 e il divisore è diverso da 0 allora il
quoziente è uguale 0:
0 : 12 = 0
Se il divisore è uguale a 0 e il dividendo è diverso da 0 allora la
divisione è impossibile
12 : 0 = impossibile
Se il divisore è uguale a 0 e il dividendo è uguale a 0 allora la
divisione è indeterminata
0 : 0 = indeterminata