trasparenze ppt

Rotazione di un corpo rigido attorno
ad un asse fisso
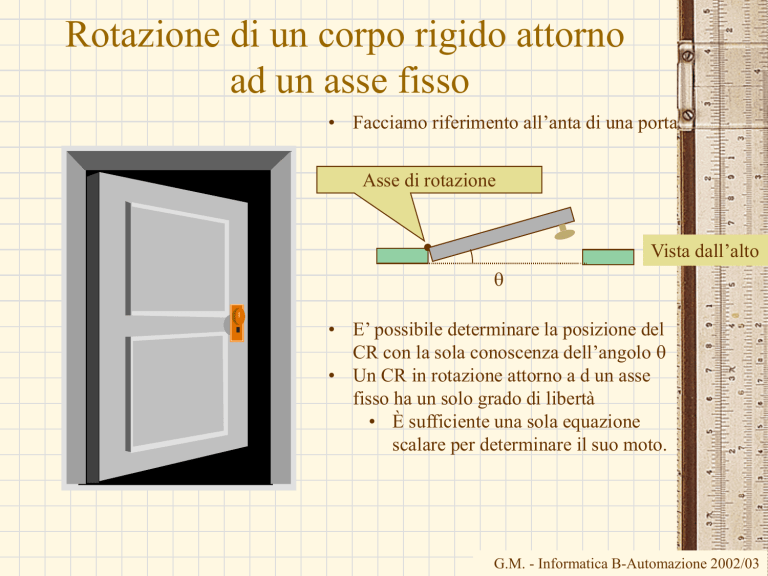
• Facciamo riferimento all’anta di una porta
Asse di rotazione
Vista dall’alto
q
• E’ possibile determinare la posizione del
CR con la sola conoscenza dell’angolo q
• Un CR in rotazione attorno a d un asse
fisso ha un solo grado di libertà
• È sufficiente una sola equazione
scalare per determinare il suo moto.
G.M. - Informatica B-Automazione 2002/03
Rotazione di un corpo rigido attorno
no ad un asse fisso
• Cerchiamo quindi una relazione tra le forze applicate e l’accelerazione
(angolare) prodotta.
q
Vista dall’alto
• Nel caso della rotazione la forza non è
direttamente responsabile dell’effetto prodotto.
• Supponiamo di applicare forze perpendicolari al
piano della porta:
• Se applichiamo una forza a distanza nulla d’asse
di rotazione:
• l’effetto è nullo: non c’è nessun moto
• Man mano che ci allontaniamo dall’asse di
rotazione, a parità di forza, l’effetto
(l’accelerazione angolare della porta ) è sempre
più vistoso
•
Ecco perché la maniglia si mette il più lontano
possibile dall’asse di rotazione
G.M. - Informatica B-Automazione 2002/03
Rotazione di un corpo rigido attorno
no ad un asse fisso
• Sembra quindi che l’effetto, l’accelerazione (angolare) prodotta, dipende dal
prodotto della forza per il braccio
• Braccio=distanza della retta di azione della forza d’asse di rotazione
O
b
r
q
O
r
F
F
Vista dall’alto
• L’effetto, l’accelerazione (angolare) prodotta,
sembra dipendere dal momento della forza
rispetto al polo O
• Il modulo del momento vale infatti:
Mo  r  F  Frsen  Fb
• Si osservi che in questo caso il momento della
forza è parallelo all’asse di rotazione
G.M. - Informatica B-Automazione 2002/03
Rotazione di un corpo rigido attorno
no ad un asse fisso
• Possiamo ulteriormente investigare questa conclusione facendo variare
l’angolo  della forza rispetto al vettore posizione mantenendo la forza nel
piano perpendicolare all’asse di rotazione

b
b
O r
F
q
O
r
F
Vista dall’alto
• L’effetto è maggiore quando l’angolo  è 90°
• È nullo quando  è 0° o 180°
• Questa osservazione ci conferma che la causa
delle rotazioni è il momento della forza.
• Infatti:
Mo  r  F  Frsen  Fb
• Che è massimo quando  è 90°, è nullo quando
 è 0° o 180°
• Si osservi che anche in questo caso il momento
della forza è parallelo all’asse di rotazione
G.M. - Informatica B-Automazione 2002/03
Rotazione di un corpo rigido attorno
no ad un asse fisso
• Concludiamo questo discorso considerando forze nel piano della porta.
• Se consideriamo una forza perpendicolare al vettore posizione r
•
Il modulo del momento è
Mo  r  F  Frsen  Fb
• Lo stesso modulo del momento quando la forza
F è perpendicolare al piano della porta
• Ma in questo caso l’effetto prodotto è nullo!!
•
F
O
r
Non si verifica alcun moto della porta.
• Cosa c’è di diverso nei due casi??
• Osserviamo che in questo caso il momento Mo è
perpendicolare all’asse di rotazione
•
In precedenza esso era parallelo all’asse di
rotazione
• Possiamo concludere:
• Il moto di rotazione di un corpo rigido
attorno ad un asse fisso dipende dalla
componente del momento della forza lungo
l’asse di rotazione (Momento assiale)
G.M. - Informatica B-Automazione 2002/03
Equazione del moto di rotazione di un
corpo rigido attorno ad un asse fisso
• Abbiamo dedotto:
– il moto di rotazione di un corpo rigido attorno ad un asse fisso dipende dal
momento assiale (la componente del momento delle forze esterne lungo
l’asse di rotazione)
• Si trova infatti che:
I  Mz
Equazione del moto di rotazione di un CR
attorno ad un asse fisso
•
I = momento di inerzia del CR rispetto all’asse
di rotazione
•
 accelerazione angolare
•
Mz componente assiale del momento delle forze
esterne
G.M. - Informatica B-Automazione 2002/03
Verifica dell’equazione del moto di rotazione
di un CR rispetto ad un asse fisso
• Consideriamo un caso semplice in cui un corpo rigido è costituito da un
singolo punto materiale in rotazione attorno ad un asse fisso (l’asse z).
•
Il momento della forza F rispetto al punto
O è:
M  rF
o
•
Il cui modulo è:
•
Il momento è diretto parallelamente
all’asse z
M z  Mo  Ft r
•
•
La componente radiale della forza non
produce alcun effetto perché l’asta
provvede ad annullare il suo effetto (la
distanza dall’asse di rotazione deve
rimanere costante).
Invece la componente tangente: Ft  ma t  mr
•
Moltiplicando per r:
Mo  r  F  Frsen  Ft r
Ft r  mr 
2
M z  I
G.M. - Informatica B-Automazione 2002/03
Legame tra l’equazione del moto di rotazione del CR
e la II equazione cardinale della dinamica dei sistemi
•
Consideriamo un sistema di punti
materiali, rigido, in rotazione attorno
all’asse z con velocità angolare w.
Consideriamo la particella i-esima.
•
z
vi
P
i
P'
i
j
ri
vettore posizione
Ri
distanza dall' asse di rotazione
v i  wR i
modulo della velocità
i
 ri  m i v i
 rim i v i  ri m iwR i
iz  i cos 90  qi  
qi
i
momento della quantità di moto
i
Ri
ri
j
O
y
modulo del momento della quantità di moto
x
 m i wR i ri sen qi  m i R2i w componente assiale
n
Lz 

i1
•
Ri
iz
n


i1
 n

2
2
m i Ri w   m i R i w  Iw
 i1


Se il corpo è simmetrico rispetto all’asse
di rotazione: Lx=0, Ly=0
dL o
dLz
 Mo 
 Mz
dt
dt
dL z dIw 


dt
dt Icos t
L z  Iw 
dw
I
 I  Mz
G.M. - Informatica B-Automazione
2002/03
dt
Calcolo del momento assiale delle forze
metodo 1
z asse di rotazione
•
•
•
•
Il primo metodo consiste nello scegliere un
qualsiasi polo O sull’asse di rotazione (punto
fisso)
Calcolare il momento di ciascuna forza esterna
rispetto al polo O (modulo direzione e verso)
Calcolare il momento risultante
Determinare la componente del momento
risultante secondo l’asse di rotazione


Mo  r  F
F
O
r
F
b
F
x

Mo  r  F  r  r  F  F  r  F  r  F  r  F  r  F
 all' asse
•
 all'asse
y
retta di azione diF
 M z  F b
 all' asse
Il momento assiale di una forza non dipende dal polo O scelto per
O’
calcolarlo.
Mo  r  F
M o'  r'  F Perpendicolare a OO’
r’
F
M o  Mo'  r  F  r' F  r  r'   F  OO' F
O
r
• I due momenti differiscono per un vettore
perpendicolare all’asse: questo vuol dire che le
componenti assiali sono uguali.
G.M. - Informatica B-Automazione 2002/03
Calcolo del momento assiale delle forze
metodo 2
M  r  F  r  r  F  F  r  F  r  F  r  F  r  F

o



 all' asse
•
•
•
 all'asse


M z  F b
 all' asse
si prende il modulo del vettore componente della
forza nel piano perpendicolare all’asse di rotazione.
Si moltiplica tale modulo per il braccio della forza
(la distanza tra la retta di azione del vettore
componente della forza perpendicolare all’asse di
rotazione e l’asse di rotazione)
Si assegna a questo prodotto il segno positivo se la x
forza produce una rotazione antioraria, negativo se la
rotazione prodotta è oraria.
F b
M z  
F b
•

z
asse di rotazione
Mz  Fb
F
b
F
z
rotazione antioraria
(rotazione antioraria)
y
retta di azione diF
asse di rotazione
y
b
rotazione oraria
Il momento assiale complessivo si
ottiene sommando i singoli contributi
di ciascuna delle forze esterne agenti:
F
n um fo rze
Mz 
M
i1
retta di azione diF
iz
x
Mz  Fb
(rotazione
antioraria)
G.M. - Informatica
B-Automazione
2002/03
•
La figura rappresenta un disco uniforme di massa M=2.5 kg e raggio R=20 cm
montato su un mozzo orizzontale fisso. Un blocco di massa M=1.2 kg è appeso
Applicaz
ad un filo privo di massa avvolto intorno al bordo del disco. Trovare
ione
l’accelerazione di caduta del blocco, l’accelerazione angolare del disco e la
tensione del filo. Il filo non slitta e il mozzo gira senza attrito. y
•
Rv
•
Il moto del disco è un moto di rotazione
attorno ad un asse fisso
Introduciamo un sistema di riferimento
•
•
L’asse di rotazione coincide con l’asse z
L’equazione del moto di rotazione M
•
Il momento di inerzia I (disco omogeneo
rispetto al suo asse)
1
1
2
2
2
I  MR   2.5kg  .20m  .05kgm
2
2
•
Dobbiamo ora calcolare Mz:
x
P
z  I
– Le forze esterne agenti sul disco sono
tensione
MzT  TR
peso
MzP  0
reazione vincolare
MzR v  0
•
L’equazione del moto:
1
2
 TR  MR 
2
G.M. - Informatica B-Automazione 2002/03
•
La figura rappresenta un disco uniforme di massa M=2.5 kg e raggio R=20 cm
montato su un mozzo orizzontale fisso. Un blocco di massa M=1.2 kg è appeso
Applicaz
ad un filo privo di massa avvolto intorno al bordo del disco. Trovare
ione
l’accelerazione di caduta del blocco, l’accelerazione angolare del disco e la
tensione del filo. Il filo non slitta e il mozzo gira senza attrito. y
•
Per il corpo di massa m invece:
T  Fg  ma
y
Rv
T  mg  ma y
x
1
 TR  MR2 
2
T  mg  ma y
•
Abbiamo ottenuto due
equazioni con le
incognite T, ay, .
•
•
•
Le equazioni non sono sufficienti.
Ma sappiamo che la corda è inestensibile
quindi c’è una relazione tra ay, .
Ruotiamo il disco di un angolo Dq in senso
antiorario (Dq negativo), osserveremo il
corpo di massa m abbassarsi di un tratto Dy
anch’esso negativo:
Dy  RDq
•
Dividendo per Dt, e passando al limite
Dy
Dq
R
 v y  Rw
Dt
Dt
P
•
E con una seconda derivazione si ottiene
a y  R
G.M. - Informatica B-Automazione 2002/03
•
•
•
La figura rappresenta un disco uniforme di massa M=2.5 kg e raggio R=20 cm
montato su un mozzo orizzontale fisso. Un blocco di massa m=1.2 kg è appeso
ad un filo privo di massa avvolto intorno al bordo del disco. Trovare
l’accelerazione di caduta del blocco, l’accelerazione angolare del disco e la
tensione del filo. Il filo non slitta e il mozzo gira senza attrito. y
1
Il sistema diventa
 TR  MRa y
2
T  mg  ma y
x
1
O meglio:
 T  Ma y
2
T  mg  ma y
Sostituendo:
1
T   Ma y
2
1
 Ma y  mg  ma y
2
Applicaz
ione
Rv
P
•
1
T   Ma y
2
1

 mg  m  M
a
2  y
mg
1.2  9.81 11.7



 4.77 m 2
1
1
s
m  2M
1.2  2  2.5
2.45
1
T   Ma y   12  2.54.77  5.96N
2
ay 

ay
R

4.77 m
.20m
s2  23.8 rad
s2
G.M. - Informatica B-Automazione 2002/03
Il lavoro nei moti di rotazione
•
Facendo riferimento all’applicazione precedente
calcoliamo il lavoro infinitesimo fatto dalla tensione T
relativamente ad uno spostamento angolare infinitesimo
dq:
dq
dW  T  dr  Tds cos   T Rdq   TRd q  M z dq
•
Nel caso della figura ds, il modulo dello spostamento
infinitesimo, è uguale a -Rdq (il segno meno si giustifica per
il fatto che dq è negativo, mentre ds deve essere positivo)
•
Il lavoro per una rotazione finita sarà:
W
•
qf
 M dq
qo
z
La potenza:
P
dW
dq
 Mz
 M zw
dt
dt
Si osservi che poiché la corda è
inestensibile il lavoro
complessivo fatto dalle due
tensioni ai due capi della corda è
nullo.
dr
dr1
dr2
G.M. - Informatica B-Automazione 2002/03
•
Con riferimento all’applicazione precedente in cui un disco uniforme di massa
M=2.5 kg e raggio R=20 cm montato su un mozzo orizzontale fisso e un
blocco di massa m=1.2 kg è appeso ad un filo privo di massa avvolto intorno
al bordo del disco, calcolare la velocità del corpo di massa m dopo che ha
percorso 1m supponendo che inizialmente fosse fermo.
Calcolare la corrispondente velocità angolare del disco.
Calcolare l’angolo di cui ha ruotato il disco.
Verificare che il lavoro fatto dalla tensione sul disco
è uguale alla variazione della sua energia cinetica.
y
•
•
•
•
Noi abbiamo già calcolato l’accelerazione
uniforme del corpo di massa m.
Potremmo risolvere il problema per via
cinematica:
2
2
v  v o  2a y (y  y o )

v  24.771  3.1 m s
•
Applicaz
ione
Rv
x
P
v 3.1 m s
w 
15.5 rads
R 0.2m
•
Possiamo anche risolvere il problema con la
conservazione dell’energia:
DE  Wnc  WT1  WT2 
0
WR v
0
app . a un punto fermo
•
La forza peso della carrucola non fa
lavoro
G.M. - Informatica B-Automazione 2002/03
•
Con riferimento all’applicazione precedente in cui un disco uniforme di massa
M=2.5 kg e raggio R=20 cm montato su un mozzo orizzontale fisso e un
blocco di massa m=1.2 kg è appeso ad un filo privo di massa avvolto intorno
al bordo del disco, calcolare la velocità del corpo di massa m dopo che ha
percorso 1m supponendo che inizialmente fosse fermo.
Calcolare la corrispondente velocità angolare del disco.
Calcolare l’angolo di cui ha ruotato il disco.
Verificare che il lavoro fatto dalla tensione sul disco
è uguale alla variazione della sua energia cinetica.
y
•
•
•
DE  Wnc  WT1  WT2 
0
WR v
mgh 
Rv
0
app . a un punto fermo
Ei  Ef  K i  Ui  K f  Uf
0  mgh 
Applicaz
ione
x
P
1
1 2
2
mv  Iw  0
2
2
1 2 11
1 
1
2 2
2
mv 
MR w  m  M
v
2
22
2
2 
2
v
2mgh
2  1.2  9.81  1
m2
v 

 9.6 2
1 
1 


s
m M
1.2  2.5


2 
2 
2
m
m2
m w  v  3.1 s 15.5 rad
s
v  9.6 2  3.1
R 0.2m
s G.M. - Informatica
s
B-Automazione 2002/03
•
Con riferimento all’applicazione precedente in cui un disco uniforme di massa
M=2.5 kg e raggio R=20 cm montato su un mozzo orizzontale fisso e un
blocco di massa m=1.2 kg è appeso ad un filo privo di massa avvolto intorno
al bordo del disco, calcolare la velocità del corpo di massa m dopo che ha
percorso 1m supponendo che inizialmente fosse fermo.
Calcolare la corrispondente velocità angolare del disco.
Calcolare l’angolo di cui ha ruotato il disco.
Verificare che il lavoro fatto dalla tensione sul disco
è uguale alla variazione della sua energia cinetica.
y
•
•
•
Dq 
h
1m

 5rad
R 0.2m

•
P
1
2
2
 2.5  .2  15.5  6.0J
4
Ricordiamo il valore della tensione T
determinato precedentemente (T=5.96N)
WT 
•
Rv
x
1 2 11
2 2
Iw 
MR w 
2
22
DK  K f  Ki 
Applicaz
ione
q
q
 M dq   TRdq  TRDq  5.96  .2  5  5.96J
0
z
0
Per il teorema delle forze vive:
DK  Wrisul tante  WT WP  WR v
0
G.M. - Informatica B-Automazione 2002/03