Dinamica dei Fluidi

UNIVERSITÀ DEGLI STUDI DI CATANIA
SCUOLA INTERUNIVERSITARIA SICILIANA DI SPECIALIZZAZIONE
PER L’INSEGNAMENTO SECONDARIO
DOMENICO CURRÒ
SALVATORE GRASSO
_______
DINAMICA DEI FLUIDI
________
FONDAMENTI DI FISICA I
PROF. V.BELLINI
VIII CICLO - ANNO ACCADEMICO 2006-2007
INDICE
PREREQUISITI.................................................................................................. 3
INTRODUZIONE .............................................................................................. 4
UN PÒ DI STORIA ............................................................................................ 6
MODELLI OPERATIVI .................................................................................... 9
Tipo di fluido e tipo di moto ........................................................................... 9
Linea e tubo di flusso .................................................................................... 11
DALLA CONSERVAZIONE DELLA MASSA ALL’EQUAZIONE DI
CONTINUITA’ ................................................................................................ 13
Portata ............................................................................................................ 14
Esercizio 1 ..................................................................................................... 16
DALLA CONSERVAZIONE DELL’ENERGIA ALL’EQUAZIONE DI
BERNOULLI .................................................................................................... 18
Legge di Stevino............................................................................................ 22
Legge di Torricelli ......................................................................................... 23
APPLICAZIONI DEL TEOREMA DI BERNOULLI..................................... 24
Effetto Venturi............................................................................................... 24
Tubo di Venturi ............................................................................................. 25
Esercizio 2 ..................................................................................................... 26
ALTRE APPLICAZIONI ................................................................................. 29
Spinta dinamica ............................................................................................. 29
Effetto Magnus .............................................................................................. 31
Paradosso idrodinamico ................................................................................ 32
PREREQUISITI
La presente tesina è rivolta ad alunni della terza classe di un liceo
scientifico. Per comprendere i contenuti trattati è necessaria la
conoscenza dei seguenti argomenti:
 il concetto di fluido e sue caratteristiche
 il concetto di pressione
 i principi della dinamica
 il teorema dell’energia cinetica
INTRODUZIONE
In figura richiamiamo l’attenzione su qual’è l’ambito scientifico in
cui si inserisce l’argomento da noi trattato.
Meccanica
dei fluidi
Statica
dei fluidi
Idrostatica
Statica
dei gas
Dinamica
dei fluidi
Idrodinamica
Dinamica
dei gas
La meccanica dei fluidi è quel ramo della fisica che si occupa del
comportamento dei fluidi1, sia dal punto di vista statico che dinamico.
1
Per quanto riguarda le caratteristiche di un fluido esso può essere viscoso o non viscoso; la viscosità è per i
fluidi l’analogo dell’attrito per i solidi, quindi un fluido non viscoso è un fluido privo di attrito interno. Inoltre, un
fluido può essere comprimibile o incomprimibile se la sua densità è, rispettivamente, dipendente o indipendente
sia dalla posizione che dal tempo.
Riteniamo opportuno osservare che, nonostante l’apparente
settorializzazione, i risultati ottenuti in idrodinamica vengono utilizzati
correntemente anche nel caso dei gas che in particolari condizioni (basse
velocità, variazioni di pressione trascurabili) possono essere considerati
sostanzialmente incomprimibili e quindi trattati alla stregua dei liquidi.
Storicamente la dinamica dei fluidi è stata affrontata con due
approcci diversi, noti rispettivamente come punto di vista lagrangiano e
punto di vista euleriano.
Nel punto di vista lagrangiano si divide il fluido in volumi
infinitesimi, chiamati particelle di fluido, e si considera il moto di una
particella di fluido, all’interno del fluido stesso, sotto l’azione della
gravità, della pressione esterna, ecc. Dovremmo dare le coordinate x, y e
z di ciascuna particella e precisare il comportamento in funzione del
tempo t. Questo procedimento è una diretta generalizzazione dei concetti
della meccanica del punto materiale. A causa del grandissimo numero di
particelle, l’uso di questo metodo è un’impresa improba.
Nel punto di vista euleriano, anziché descrivere la storia di ogni
singola particella di fluido si valutano la densità, la pressione e la velocità
in ogni punto dello spazio e in ogni istante; si fa riferimento al cosiddetto
volume di controllo, regione dello spazio che in istanti diversi viene
occupata da particelle diverse.
Entrambi i metodi portano alle stesse conclusioni fisiche, ma il
punto di vista euleriano, risulta più conveniente nell’uso comune.
Sovente nella società moderna si sente dire: “Chi diavolo ce l’ha portato un
ingegnere civile ad insegnare fisica in un istituto tecnico?” Ebbene, un attento
sguardo alla storia ci mostra esempi di applicazioni della fluidodinamica che
spaziano dal campo della medicina, all’ingegneria, al campo agricolo. Li
segnaliamo semplicemente, ma intendiamo qui sottolineare quanto sia
importante lo scambio di contributi tra diverse discipline e tra diversi campi
della scienza.
UN PÒ DI STORIA
L’interesse per la meccanica dei fluidi risale alle primissime
applicazioni ingegneristiche delle proprietà dei fluidi e alla necessità di
realizzare delle macchine adibite a varie funzioni. Archimede (287-212
a.C.) fornì probabilmente il primo contributo in questo campo con
l’invenzione della pompa a vite.
Altre macchine idrauliche vennero
in seguito costruite dai romani che,
non solo adottarono la vite di
Archimede per l’irrigazione e per
l’estrazione dell’acqua dai pozzi,
ma costruirono nuovi sistemi
idraulici, alcuni dei quali sono
Vite di Archimede
tuttora in uso. Nel corso del I secolo
a.C. l’architetto e ingegnere romano Vitruvio introdusse la ruota
idraulica, una macchina che rivoluzionò il sistema di macinazione del
granturco.
Gli ulteriori sviluppi in questo campo furono
ritardati dal fatto che, nonostante le numerose
precoci applicazioni della fluidodinamica, poco o
nulla si sapeva allora dei suoi principi teorici
fondamentali. Dopo il contributo di Archimede,
dovettero passare più di 1800 anni prima che
venisse compiuto un significativo progresso. Ciò
avvenne per merito di Evangelista Torricelli (16081647), il quale nel 1643 inventò il barometro e
formulò un’importante legge tuttora nota con il
Fig. 1. Evangelista
suo nome.
Torricelli
I successivi progressi della meccanica
dei fluidi si ebbero per opera di due
matematici svizzeri Daniel Bernoulli (17001782) e Leonhard Euler (1707-1783). Il primo
scrisse nel 1738 il trattato “Hydrodynamica,
sive de viribus et motibus fluidorum
commentarii”, nel quale risolse molti
problemi concreti di dinamica dei fluidi e
dimostrò
una
famosa
legge
di
conservazione che porta il suo nome.
Fig. 2. Daniel Bernoulli
Eulero nel 1755, applicando allo studio dei
fluidi i tre principi della dinamica enunciati
da Isaac Newton, scrisse le equazioni
fondamentali per il moto di fluidi ideali,
cioè non viscosi. Eulero per primo
riconobbe, inoltre, che l’unica possibilità di
enunciare leggi relativamente semplici per
la dinamica dei fluidi fosse quella di
limitare lo studio ai fluidi incomprimibili e
Fig. 3. Leonhard Euler
ideali, ossia di trascurare gli effetti
dell’attrito interno.
Naturalmente, essendo i fluidi ideali mere approssimazioni dei
fluidi reali, i risultati dell’analisi di Eulero possono essere considerati solo
una stima approssimata del comportamento di fluidi reali caratterizzati
da bassi valori di viscosità. I primi esperimenti sul moto a bassa velocità
di fluidi viscosi furono condotti nel 1839 dal fisiologo Jean-LèonardMarie Poiseuille (1799-1869), interessato a determinare le proprietà della
circolazione del sangue, e nel 1840 dall’ingegnere idraulico tedesco
Gotthilf-Heinrich-Ludwig Hagen (1797-1884). I primi tentativi di
includere gli effetti della viscosità nelle equazioni matematiche del moto
dei fluidi si devono invece all’ingegnere francese Claude-Louis-Marie
Navier (1785-1836), e al matematico britannico George Gabriel Stokes
(1819-1903) il quale, nel 1845 formulò le equazioni fondamentali per i
fluidi viscosi incomprimibili.
MODELLI OPERATIVI
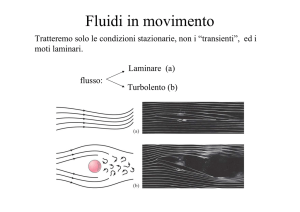
Tipo di fluido e tipo di moto
Nella nostra trattazione ci occuperemo di trattare principalmente:
 Fluido ideale, ovvero incomprimibile e non viscoso
 Moto stazionario e irrotazionale
Ritenendo già acquisito il concetto di fluido, per comprendere bene
la natura di alcune semplificazioni che faremo, bisogna introdurre
qualche cenno sulle caratteristiche generali del moto dei fluidi.
Abbiamo visto che il punto di vista euleriano studia il moto di un
fluido valutando variabili come pressione, densità e velocità nel volume
di controllo. Il legame di queste variabili con il tempo comporta la
distinzione in:
 moto stazionario: pressione, densità e velocità si mantengono costanti
nel tempo; in generale il loro valore varia da punto a punto, ma in un
certo punto non varia. Di solito questa condizione è ottenuta a basse
velocità di flusso; per esempio in un canale con una corrente molto lenta;
 moto non stazionario: se pressione, velocità e densità variano nel
tempo, per ogni punto. Le onde del mare sono un esempio di questo tipo
di moto. Se queste grandezze variano in modo irregolare, il moto si dice
più propriamente turbolento; esempi sono le rapide e le cascate.
Si può definire il moto di un fluido a seconda delle caratteristiche
assunte dalla velocità angolare degli elementi costituenti il fluido stesso:
 moto irrotazionale: nel fluido in moto non c’è alcun elemento in
rotazione attorno ad un asse passante per il centro di massa dell’elemento
stesso;
 moto rotazionale: gli elementi di fluido hanno velocità angolare non
nulla attorno ad un asse passante per il rispettivo centro di massa.
Ad esempio, una piccola ruota a palette immersa in un fluido in
moto ruota solo se il flusso è rotazionale, altrimenti trasla senza ruotare.
Fig. 4. -
Ruota con palette immersa in un fluido in moto
È importante notare che l’irrotazionalità del moto non dipende
dalla traiettoria della particella di fluido. Un particolare elemento di
fluido può muoversi, infatti, su una traiettoria circolare ma il moto può
essere lo stesso irrotazionale
Fig. 5. -
Moto irrotazionale su traiettoria circolare
Allo stesso modo, una particella di fluido può seguire una
traiettoria rettilinea pur avendo un moto rotazionale
Fig. 6. -
Moto rotazionale lungo traiettoria rettilinea
Linea e tubo di flusso
Se il moto è stazionario la velocità v in ogni punto è costante nel
tempo, cioè ogni particella che transita per un qualsiasi punto P lo fa
sempre con la stessa velocità in modulo, direzione e verso. Lo stesso vale
per i punti Q ed R, perciò se tracciamo il percorso di una particella,
questo sarà anche il percorso di ogni altra particella che arriva in P. La
curva che descrive il moto della particella si chiama linea di flusso ed è
tangente alla velocità della particella in ogni suo punto
Fig. 7. -
Linea di flusso
Le linee di flusso possono essere evidenziate nell’acqua che scorre
in un condotto iniettando in vari punti del condotto piccole quantità di
liquido colorato oppure mettendo dei corpi leggeri come segatura o
sferette di plastica.
Nel moto stazionario le linee di flusso non si incrociano mai in
quanto, se lo facessero, una particella che arriva al punto di incrocio
potrebbe proseguire lungo una linea o l’altra, quindi in uno stesso punto
potrebbe avere differenti valori di velocità, contrariamente all’ipotesi
stessa di stazionarietà. È possibile quindi dire che per il moto stazionario
esiste una sola linea di flusso per ogni punto del fluido e che l’insieme
delle linee di flusso è fisso nel tempo.
Prendendo un fascio di linee di flusso otteniamo una superficie
tubolare detta tubo di flusso
Fig. 8. -
Tubo di flusso
Per semplicità d’ora in avanti faremo coincidere il tubo di flusso
con il condotto reale entro il quale scorre il fluido.
DALLA CONSERVAZIONE DELLA MASSA
ALL’EQUAZIONE DI CONTINUITA’
Si consideri una porzione di un generico tubo di flusso (Figura 9).
Siano A1, ρ1 e v1 la sezione, la densità e la velocità del fluido all’estremità 1
e A2, ρ2 e v2 quelle all’estremità 2. Nell’intervallo di tempo Δt sarà passato
un volume di fluido V1  A1v1t , attraverso la sezione 1 e V2  A2 v2 t
attraverso la sezione 2.
Poiché le pareti del tubo sono rigide e impermeabili al fluido e non
vi sono all’interno ne sorgenti ne pozzi dove il fluido possa essere creato
o distrutto, la massa di fluido che attraversa la sezione A1 nell’intervallo
Δt con velocità v1 deve essere uguale alla massa che attraversa la sezione
A2 nello stesso intervallo Δt con velocità v2, cioè Δm1 = Δm2.
Fig. 9. -
Tubo di flusso a sezione variabile
Esprimendo la massa come prodotto della densità e del volume,
m  V , ed eliminando il fattore comune Δt si avrà:
1 A1v1   2 A2 v2 .
Per l’incomprimibilità del fluido ρ1 = ρ2, quindi
A1v1=A2v2.
Poiché questo discorso può essere fatto per due sezioni qualsiasi,
sarà:
Av = costante
Questa equazione è detta equazione di continuità.
Una immediata interpretazione è che la variazione della velocità nel
tubo di flusso è inversamente proporzionale alla sua sezione. Applicata
ad un tubo di flusso, questa relazione ci consente di interpretare
ulteriormente la rappresentazione con linee di flusso del moto di un
fluido. Tali linee si addensano dove il tubo è stretto e si diradano ove il
tubo è largo. Dunque la distanza tra le linee di flusso è piccola laddove la
velocità del fluido è grande e viceversa.
Fig. 10. -
Le linee di flusso in condotto a sezione variabile
Portata
Il prodotto Av, che misura un flusso di volume, permette di
introdurre una grandezza molto usata in fluidodinamica: la portata.
Si definisce portata in massa il rapporto tra la massa di fluido che
attraversa una sezione e l’intervallo di tempo impiegato,
m V AS
Qm 


 Av
t
t
t
Nel Sistema Internazionale si misura in kg/s.
Analogamente, si definisce portata in volume il rapporto tra il
volume di fluido che attraversa una sezione e l’intervallo di tempo
impiegato:
Qv 
V AS

 Av
t
t
3
Nel Sistema Internazionale si misura in m /s.
Il concetto di portata in volume ci consente di scrivere l’equazione
di continuità nella forma:
Qv  cos tan te .
Applicazione
Una tipica applicazione dell’equazione di continuità si osserva in
un getto d’acqua che fuoriesce da un rubinetto. La sua velocità cresce
man mano che il getto cade: poiché la portata deve essere la stessa in
tutte le sezioni, lungo la caduta il getto si deve assottigliare
Fig. 11. -
Sezione del tubo di flusso in getto d’acqua in caduta
In alcuni tipi di fontane avviene esattamente il contrario. Lo
zampillo che sale verso l’alto perde man mano velocità, per cui, ancora
per l’equazione di continuità la sezione del getto aumenta.
Esercizio 1
Uno scultore sta lavorando ad un balenottero da porre al centro di
una fontana. Dalla bocca della statua fuoriuscirà il getto d’acqua della
fontana. Lungo il corpo del balenottero verrà immesso un tubo di sezione
A=3.14 cm2 nel quale confluirà l'acqua alla velocità di v=90.0 cm/s.
Si vuole dimensionare la sezione del tubo in prossimità della bocca
del balenottero in modo che il getto d’acqua uscente dovrà raggiungere
un punto della fontana distante d=60.0 cm e che si trova ad un'altezza di
h=120.0 cm al di sotto della bocca stessa. Che diametro D dovrà dare a
questa lo scultore?
Soluzione
L’acqua uscirà formando un tubo di flusso con traiettoria
parabolica per la quale valgono le seguenti relazioni note dalla meccanica
classica:
d  v' t
g


1 2  v'  d
2h
h  gt


2
Ora, applicando l'equazione di continuità, si ricava la nuova
sezione A' in funzione di A, v, v'
A' v'  Av
ovvero: A’= 2,33 cm2
A'
D
4A'

Av 2h
d
g
D=1,7 cm
DALLA CONSERVAZIONE DELL’ENERGIA
ALL’EQUAZIONE DI BERNOULLI
L’equazione di Bernoulli è di fondamentale importanza nella
dinamica dei fluidi. Come tutte le equazioni della meccanica dei fluidi
essa non costituisce un nuovo principio, ma è derivabile come
conseguenza delle leggi della meccanica newtoniana. Risulta comodo
ricavarla dal teorema dell’energia cinetica, poiché essenzialmente essa
rappresenta la formulazione del teorema della conservazione dell’energia
nel caso del moto di un fluido.
Consideriamo ancora un fluido ideale (cioè incomprimibile e non
viscoso) che scorre di moto stazionario in un tubo di sezione e quota
variabile.
Fig. 12. -
Moto in un tubo di sezione e quota variabile
La porzione di tubo rappresentata in figura ha, nella sua prima
parte una sezione A1 costante e orizzontale, e si trova a un’altezza y1
rispetto ad un livello di riferimento. Il tubo poi gradualmente si restringe
e si innalza sinchè infine, sulla destra vi è di nuovo una parte orizzontale
a sezione A2 costante e ad un altezza y2. Concentriamo la nostra
attenzione sulle porzioni di fluido che in figura sono ombreggiate.
Queste porzioni di fluido costituiscono il nostro sistema e ne vogliamo
studiare il moto che lo fa passare dalla configurazione disegnata in (a) a
quella in (b). Il disegno rappresenta l’effetto risultante dallo scorrimento
del fluido nel condotto ovvero il sollevamento della quantità Δm di fluido
ombreggiata. Dall’ipotesi di incomprimibilità segue che il volume
entrante è uguale a quello uscente e quindi tale quantità resta invariata.
Il teorema dell’energia cinetica afferma che il lavoro compiuto dalla
risultante delle forze agenti sul sistema uguaglia la variazione di energia
cinetica del sistema stesso:
L  Ec
La variazione di energia cinetica del sistema è:
Ec 
1
1
1
mv22  mv12  V (v22  v12 )
2
2
2
Se le forze agenti sul sistema sono le forze di pressione F1 ed F2
agenti rispettivamente agli estremi sinistro e destro del fluido e la forza
di gravità FP, il lavoro totale compiuto da queste forze è :
L  LP  L1  L2
La variazione di energia potenziale è:
U    V  g  ( y2  y1 )
quindi il lavoro compiuto dal campo gravitazionale è:
L p  U     V  g  ( y2  y1 )
Il fluido a sinistra dell’imboccatura del tubo che precede la massa
Δm eserciterà su essa una forza di modulo F1 = p1A1, dove p1 è la pressione
nel punto 1.
Questa forza compirà un lavoro positivo
L1  F1x1  p1 A1x1  p1V
Con un ragionamento analogo, alla fine del tubo, a destra della
massa Δm considerata, il fluido che segue compirà su di essa un lavoro
negativo
L2   F2 x2   p2 A2 x2   p2 V
dove p2 è la pressione nel punto 2 esercitata in verso contrario al
moto del fluido.
Il lavoro totale compiuto da queste forze è :
L  L1  L2  LP  p1  V  p2  V    V  g  ( y2  y1 )
Dal teorema dell’energia cinetica, uguagliando le due espressioni
ottenute, dividendo per ΔV e raccogliendo al primo membro le
grandezze relative al punto 1 ed al secondo membro quelle relative al
punto 2, si ottiene l’espressione:
1
1
p1  gy1  v12  p2  gy2  v22
2
2
Poiché i due punti sono stati presi a caso nel condotto è possibile
ripetere questo ragionamento per qualsiasi coppia di punti e quindi
concludere che
1
p  gy  v 2 = costante
2
Questa relazione è detta equazione di Bernoulli, e i termini che la
compongono sono, dimensionalmente, delle pressioni:
 la pressione p  gh , che sarebbe presente anche se non vi fosse
moto, si chiama pressione statica;
1
 il temine v 2 si chiama pressione dinamica.
2
Dividendo per ρg, si ha:
p
v2
 y
= costante
g
2g
I tre termini a primo membro hanno le dimensioni di una
lunghezza e vengono dette
p

, altezza piezometrica: è l’altezza che il fluido raggiungerebbe
g
sotto l’azione della pressione p;
 y, altezza geometrica: è l’altezza del fluido rispetto ad un livello di
riferimento;

v2
, altezza di arresto: è l’altezza che il fluido raggiungerebbe se
2g
fosse lanciato verso l’alto con velocità v.
L’equazione di Bernoulli è rigorosamente applicabile solo a moti
stazionari poiché le grandezze che intervengono devono venir valutate
lungo una stessa linea di flusso: la costante che compare nell’equazione
non è in generale la stessa per tutte le linee di flusso. Se il flusso è
irrotazionale si può dimostrare che la costante è la stessa per tutte le linee
di flusso.
L’ipotesi di incomprimibilità ci ha permesso di trascurare nei calcoli
l’energia interna del fluido, poiché essa non varia; l’ipotesi di non
viscosità ha permesso di trascurare gli attriti interni del fluido.
Si può verificare come le leggi della statica siano un caso particolare
di quelle della dinamica e si ottengono ponendo nelle equazioni v = 0. In
particolare ricaviamo di seguito la legge di Stevino e la legge di Torricelli.
Legge di Stevino
Applichiamo l’equazione di Bernoulli a due punti qualsiasi di un
recipiente contenente un fluido in quiete. I punti O e P hanno
rispettivamente altezze y1 e y2 e velocità v1 = v2 = 0.
Fig. 13. -
Fluido in quiete
Allora:
p1  gy1  p2  gy 2
da cui :
p2  p1  gy1  gy 2  g ( y1  y 2 )
che è una delle forme in cui possiamo scrivere la legge di Stevino.
Legge di Torricelli
Da un foro posto ad una distanza h dalla superficie superiore di un
fluido contenuto in un serbatoio, il fluido esce con una velocità pari a
quella che avrebbe se scendesse in caduta libera per un tratto h.
Fig. 14. -
fluido in fuoriuscita da un serbatoio
Ciò si dimostra applicando l’equazione di Bernoulli ai punti a e b
della Figura 14. Supponendo che il diametro del foro sia molto minore di
quello del serbatoio, è possibile trascurare la velocità dell’acqua in
superficie, ovvero nel punto a. L’equazione di Bernoulli diventa
1
pa  gya  pb  gyb  vb2
2
Essendo sia a che b in comunicazione con l’atmosfera, pa e pb
saranno uguali e pari alla pressione atmosferica, quindi risolvendo
rispetto vb
1
2
gya  gyb  vb2
vb2  2 g ( y a  yb ) = 2gh, da cui vb  2 gh
che è appunto la velocità che assumerebbe il fluido se cadesse da a
a b nel campo gravitazionale.
APPLICAZIONI DEL TEOREMA DI BERNOULLI
Effetto Venturi
Se la velocità di un fluido aumenta, la pressione diminuisce.
Questo fenomeno è detto effetto Venturi. Esso si dimostra applicando
l’equazione di continuità e l’equazione di Bernoulli ad un tubo con una
strozzatura orizzontale come in fig. 16.
Essendo entrambe le sezioni
alla stessa quota l’equazione di
Bernoulli non contiene il termine
1
2
gy e si riduce a: p   v 2  costante .
Fig. 15. -
Strozzatura
Tenendo presente che per il flusso di un fluido vale anche
l’equazione di continuità, essendo costante il prodotto Av, si avrà che ad
una diminuzione della sezione A corrisponde un aumento della velocità v
e, poiché la somma dei termini nell’equazione sopra deve anch’essa
rimanere costante, una diminuzione della pressione nella zona a sezione
ridotta del tubo.
Un esempio si trova nello spruzzatore
di profumi: con una pompetta in A ed il
flaconcino del profumo in B si spruzza
attraverso C.
Tubo di Venturi
Il calo di pressione nel flusso di un fluido in corrispondenza di una
diminuzione della sezione è rilevabile sperimentalmente attraverso un
apparecchio detto venturimetro o tubo di Venturi; questa informazione ci
permette anche di risalire alla velocità del fluido nel tubo.
Fig. 16. -
Tubo di Venturi
Il venturimetro è in pratica un manometro differenziale che si
immerge nel liquido del quale si vuole misurare la velocità di flusso. Il
liquido in moto ha densità ρ e fluisce in un tubo di sezione A. Il tubo
manometrico è inserito in modo che una delle due estremità sia in
corrispondenza della strozzatura di sezione a.
Applicando l’equazione di Bernoulli ai punti 1 e 2 si trova
1
1
p1  gy1  v12  p2  gy2  v22
2
2
Se il condotto è orizzontale si possono trascurare i termini ρgy che
tengono conto delle quote; inoltre, per l’equazione di continuità, nelle
due sezioni del condotto varranno le seguenti relazioni
v1A = v2a
v2 = v1(A/a)
L’equazione di Bernoulli diventa allora
1 2 1 2 1 2 2 1 2 A2
p1  p2   v2   v1   (v2  v1 )   v1 ( 2  1)
2
2
2
2
a
Se ρ’ è la densità del liquido manometrico (ad esempio mercurio),
per la legge di Stevino sarà
p1 – p2=(ρ’-ρ)gh
Uguagliando le due espressioni si ottiene:
Esercizio 2
Nella figura è rappresentato un tubo di Pitot che è un dispositivo
utilizzato per misurare la velocità v di flusso in un fluido e trova facile
applicazione nella misura della velocità aerea.
La situazione che si presenta è questa: il fluido che scorre è aria, il
liquido manometrico mercurio. Determinare la velocità del fluido
quando la differenza di altezza del liquido manometrico è h=0.65 cm.
kg

aria
:


1,
29

m3
Per le densità usiamo: 
mercurio :  '  13.600 kg

m3
Soluzione
Nel tubo di Pitot il fluido fluisce in corrispondenza delle aperture
in a
Tali aperture sono parallele alla direzione del flusso e abbastanza
lontane dall’imboccatura del tubo, in modo che velocità e pressione del
gas nelle loro vicinanze abbiano valori non perturbati dalla presenza del
tubo stesso.
Applicando l’equazione di continuità nell’imboccatura del tubo e
nel punto a, si trova che la velocità all’imboccatura si può considerare
infinitamente piccola (al limite nulla); infatti, la sezione del tubo di flusso
individuato dalle linee di flusso 1 e 2 è infinitamente grande rispetto a
quella in a. Quindi, dall’equazione di continuità
vi 
Sa
va  0
Sb
Applichiamo adesso l’equazione di Bernoulli ai punti a e b, tenendo
conto che il punto b è comunicante con l’imboccatura, pertanto la velocità
in b è nulla
1
pa   va 2  pb
2
Se h è la differenza di altezza del liquido manometrico nei due rami
e ρ’ la sua densità
pa   ' gh  pb
Confrontando le due equazioni, si ricava per la velocità dell'aria
l'espressione:
va 
2 gh '

Sostituendo i relativi valori delle densità, dell'altezza e
dell'accelerazione di gravità, si trova infine il valore cercato della velocità:
va= 1,16 m/s
ALTRE APPLICAZIONI
Spinta dinamica
È la forza che agisce su un corpo a causa del suo moto nel fluido.
Questo è l’effetto che consente agli aerei di stare sospesi in aria in quanto
fa nascere, grazie al particolare profilo delle ali, una forza che nel caso
specifico viene chiamata portanza.
Fig. 17. -
Schema generalizzato delle forze agenti su un aereo in volo
Per spiegare il fenomeno, ci poniamo in un sistema di
riferimento solidale all’aereo, così è come se l’aria andasse incontro
all’ala (schematizzata in fig. 19) da sinistra verso destra.
Il profilo alare con la sua particolare forma “a goccia” fa si che
nascano due tubi di flusso, uno superiore e l’altro inferiore:
 il tubo di flusso superiore ha una restrizione di sezione lungo il dorso
del profilo: lì la velocità aumenta perché l’aria è incompressibile. La
sua pressione di conseguenza diminuisce;
 il tubo di flusso inferiore che lambisce il ventre del profilo alare non
ha restrizioni, quindi i valori di velocità e pressione dell’aria
rimangono inalterati o quasi.
Fig. 18. -
Schematizzazione del profilo alare
Risulta quindi una pressione più piccola sul dorso dell’ala rispetto
al valore di pressione sul ventre e nasce così la spinta idrodinamica,
indicata in rosso in fig. 20: il profilo viene così “risucchiato” verso l’alto!
Fig. 19. -
Spinta idrodinamica
Un fenomeno simile avviene per le eliche, in quanto esse vengono
sagomate e disposte in modo che la spinta risulti diretta nel verso del
moto. Le pale degli elicotteri, invece, sono disposte in modo che la spinta
dinamica sia diretta verso l’alto, rendendo possibile il sostentamento del
velivolo.
Effetto Magnus
Un corpo con un moto di traslazione viene investito da una
corrente d’aria che si muove in direzione opposta a quella del corpo
stesso. Se il moto è puramente traslatorio le linee di corrente saranno
ugualmente spaziate tra loro intorno al corpo (Figura 21a). Invece, un
corpo in rotazione nell’aria, a causa dell’attrito, trascina con sé lo
straterello d’aria con cui viene a contatto; quest’ultimo a sua volta
trascina con sé lo straterello attiguo. Attorno al corpo rotante si formano
così filetti d’aria che ruotano su circonferenze concentriche (Figura 21b).
a
Fig. 20. -
b
c
La curvatura della traiettoria di un corpo dovuta all’effetto Magnus.
Se il corpo è dotato di moto sia rotatorio antiorario che traslatorio,
la velocità relativa dell’aria aumenta a sinistra del corpo proprio per il
trascinamento dell’aria attorno al corpo stesso; infatti, le velocità dei
filetti in rotazione amplificano il moto della corrente dovuto alla
traslazione se sono in verso concorde a quest’ultima, e fanno diminuire la
velocità nella zona in cui i versi sono invece discordi (Figura 21c). Per
l’equazione di Bernoulli a tale variazione di velocità corrisponde una
variazione di pressione: la traiettoria del corpo verrà quindi curvata
verso sinistra.
Paradosso idrodinamico
Una conseguenza dell’equazione di Bernoulli è il fenomeno che va
sotto il nome di paradosso idrodinamico. Supponiamo di soffiare attraverso
il tubo: si crea quindi una corrente fluida che a forte velocità investe tra i
due dischi di sezione DD e CC (Fig. 22).
Fig. 21. -
Paradosso idrodinamico.
Contrariamente a quanto potremmo aspettarci il piatto CC non
viene respinto dalla corrente fluida uscente dal tubo, ma viene attratto
verso DD. Infatti, l’aria passa nel tubo con una certa velocità v0, maggiore
della velocità del fluido in quiete esterno ai dischi. La pressione
all’interno sarà quindi minore di quella esterna e causa l’avvicinamento
dei due dischi.