Fis_gen_esame_18-09-08 - Università degli Studi di Roma "Tor

FISICA 1
II Prova di Settembre A.A. 2007-2008
18.09.2008
Cognome
Nome
n. matricola
Corso di Studi
Docente
Voto
Quesito n. 1 Nell’oscillazione di un pendolo dove è massima l’accelerazione radiale? Spiegare. Quale è l’espressione
del rapporto tra massima accelerazione radiale e massima accelerazione tangenziale?
Accelerazione radiale v2 /R, dunque massima al centro dell’oscillazione.
Facendo il confronto tra i massimi (per piccole oscillazioni),
(an )max / (a ) max = g l (1-cos(0 ))/g l sin(0 ) 1-(1+0 2)/0 = 0 , ampiezza angolare dell’oscillazione.
Quesito n. 2 Una palla rimbalza su un pavimento orizzontale. Con riferimento al vettore quantità di moto q della palla,
quale delle seguenti affermazioni è vera?
1. Si conserva solo nel caso di urto elastico.
2. Si conserva in ogni caso.
3. Perché si conservi, l’incidenza deve essere normale.
4. Non si conserva mai.
Spiegare.
4 (si conserva solo la quantità di moto totale q+Q, con Q riferita alla Terra).
Quesito n. 3 Scrivere l’enunciato del 2° principio della termodinamica in termini dell’entropia, e spiegarne il significato..
S≥ 0 dove S = entropia dell’universo.
Esercizio n. 1 Un’automobile deve trascinare un carrello di massa M lungo una strada in salita priva di attrito essendo
collegata al carrello tramite una molla di costante elastica K. La pendenza è = 10°. Quali sono i valori massimi di velocità
e accelerazione dell’auto, perché l’allungamento della molla non superi il valore massimo LM ? Eseguire i calcoli per M=
200 Kg, K= 1000 N/m, LM= 0.5 m.
Per il carrello si ha, per il massimo allungamento consentito della molla,
MaM = KLM - Mg sin
Quindi la velocità è indifferente mentre l’accelerazione massima è
aM = KLM /M - g sin  = 0.8 m/s2.
Esercizio n. 2 Da una molla pende verticalmente verso il basso un peso di massa M. Ne risulta una elongazione l della
molla all’equilibrio. Al peso viene poi improvvisamente impressa una velocità V diretta verso l’alto provocando
l’innalzamento della massa per un tratto L. Si calcolino il valore di L e dell’impulso J che è necessario trasferire al peso per
imprimergli la velocità iniziale V. Effettuare i calcoli per M = 10 kg, l =80 cm, V= 3.5 m/s
Dalla condizione di equilibrio iniziale si ricava K = Mg/l, mentre dopo che è stata impressa la velocità V per la conservazione
dell’energia meccanica si ha
½MV2 + ½Kl2 = ½K(l - L)2 + MgL
da cui si ricava L= V(l/g)0.5= 1 m.
Infine, J= MV=35 Ns .
Esercizio n. 3 Una mole di gas ideale monoatomico è contenuta all’interno di un cilindro di raggio R, chiuso da un
pistone libero di muoversi, di massa m. Esternamente, la pressione è quella atmosferica p0. La temperatura iniziale del gas
è quella ambiente (T0= 300 K). Ad un certo istante, il gas viene riscaldato irreversibilmente fino ad aumentare la sua
temperatura di T. Calcolare il volume finale e la variazione di entropia della trasformazione irreversibile effettuata dal gas.
Svolgere i calcoli per R = 2 cm, m = 7 kg, T=120°C.
La trasformazione del gas è isobara alla pressione
p= p0+mg/R2 = 1.53 atm.
Mentre la temperatura finale è Tf= 420 K.
Allora Vf = RTf /p = 22.54 l
E calcolando la variazione di entropia su una isobara reversibile
S = cp ln(Vf/Vi) = 7 J/K
FISICA 2
II Prova di Settembre A.A. 2007-2008
18.09.2008
Cognome
Nome
n. matricola
Corso di Studi
Docente
Voto
Quesito n. 1 La capacità di un condensatore dipende dal valore della costante additiva del potenziale ? Spiegare.
No, poiché C=q/V dove V è la differenza di potenziale tra le armature, indipendente dalla costante additiva.
Quesito n. 2 Per un dipolo elettrico in presenza di un campo elettrico uniforme, quante e quali posizione di equilibrio
esistono e di che tipo ( stabili o instabili)? Spiegare .
M=pESin() ; è nullo per  = 0 e  =  ; nel primo caso l’energia potenziale (U=-pECos() ) è minima (stabile) mentre nel secondo è
massima (instabile)
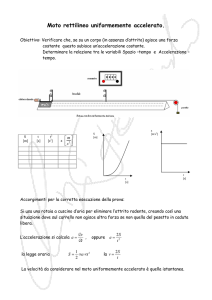
Quesito n. 3 Per quale valore del rapporto dei valori tra resistenza interna e resistenza esterna un generatore reale di
f.e.m. trasferisce sulla resistenza esterna la massima potenza? Spiegare.
Quando la resistenza elettrica del carico è uguale a quella interna del generatore.
Esercizio n. 1 Un condensatore sferico di raggi R1 e R2 =  R1 è riempito uniformemente con un dielettrico di costante
dielettrica relativa r La carica Q sulle armature del condensatore e l’energia elettrostatica W del sistema sono note.
Determinare a) la capacità C del condensatore e b) il valore di  .
Valori numerici: R1= 20 cm, r= 4, Q = 200 C ; W = 100 J.
C
4o r R1 
(  1)
W
;
1 Q2
2 C
A) C = ½ Q2/W = 0.2 nF
B)

C
 1.81
C  4o r R1
Esercizio n. 2 Con riferimento al circuito in figura, determinare le cariche che
1
passano nelle sezioni 1, 2 e 3 con i versi positivi indicati quando l’interruttore T viene
chiuso. Effettuare i calcoli per C1= 2 F, C2= 3 F, f= 60 V.
f
C1
T
3
f
C2
2
Con T aperto la carica su ognuno dei condensatori è Q  2 f
C1C2
 144C . Quando T è chiuso il
C1  C2
1
C1
f
circuito diventa quello in figura e le cariche sui condensatori diventano
Q1  fC1  120C
; Q 2  fC 2  180C
quindi nella sezione 1 passa
3
f
C2
2
fC (C  C2 )
Q1  Q  1 1
 24C ;
C1  C2
nella sezione 2 passa
Q  Q2 
fC2 (C1  C2 )
 36C ;
C1  C2
nella sezione 3 passa
f (C2  C1 )  60C.
Esercizio n. 3 Una spira piana realizzata con due maglie quadrate di lati a e b
b
(vedi figura) è immersa in un campo uniforme B (t )  B0 sin( t ) . Detta  la
resistenza per unità di lunghezza del filo della spira determinare l’ampiezza della
corrente indotta nella spira.
Eseguire i calcoli per a= 20 cm, b= 10 cm, B0= 10 mT, = 102 rad/s, = 50 /m.
b
 B(t)
a
a

f ind  a 2  b 2
 dB
 a
dt
2

 b 2 B0 cos(t )
f ind
1

(a 2  b 2 ) B0  cos(t )
R
(4a  4b)
B (a  b)
i0  0
 0,5A.
4
i (t ) 
+Q1
-Q1
+Q2
-Q2
FISICA GENERALE
II Prova di Settembre A.A. 2007-2008
18.09.2008
Cognome
Nome
n. matricola
Corso di Studi
Docente
Voto
Quesito n. 1 Nell’oscillazione di un pendolo dove è massima l’accelerazione radiale? Spiegare. Quale è l’espressione
del rapporto tra massima accelerazione radiale e massima accelerazione tangenziale?
Accelerazione radiale v2 /R, dunque massima al centro dell’oscillazione.
Facendo il confronto tra i massimi (per piccole oscillazioni),
ar / at = 0 , ampiezza angolare dell’oscillazione.
Quesito n. 2 La capacità di un condensatore dipende dal valore della costante additiva del potenziale ? Spiegare.
No, poiché C=q/V dove V è la differenza di potenziale tra le armature, indipendente dalla costante additiva.
Quesito n. 3 Per un dipolo elettrico in presenza di un campo elettrico uniforme, quante e quali posizione di equilibrio
esistono e di che tipo ( stabili o instabili)? Spiegare .
M=pESin() ; è nullo per  = 0 e  =  ; nel primo caso l’energia potenziale (U=-pECos() ) è minima (stabile) mentre nel secondo è
massima (instabile)
Esercizio n. 1 Un’automobile deve trascinare un carrello di massa M lungo una strada in salita priva di attrito essendo
collegata al carrello tramite una molla di costante elastica K. La pendenza è = 10°. Quali sono i valori massimi di velocità
e accelerazione dell’auto, perché l’allungamento della molla non superi il valore massimo LM ? Eseguire i calcoli per M=
200 Kg, K= 1000 N/m, LM= 0.5 m.
Per il carrello si ha, per il massimo allungamento consentito della molla,
MaM = KLM - Mg sin
Quindi la velocità è indifferente mentre l’accelerazione massima è
aM = KLM /M - g sin  = 0.8 m/s2.
Esercizio n. 3 Una mole di gas ideale monoatomico è contenuta all’interno di un cilindro di raggio R, chiuso da un
pistone libero di muoversi, di massa m. Esternamente, la pressione è quella atmosferica p0. La temperatura iniziale del gas
è quella ambiente (T0= 300 K). Ad un certo istante, il gas viene riscaldato irreversibilmente fino ad aumentare la sua
temperatura di T. Calcolare il volume finale e la variazione di entropia della trasformazione irreversibile effettuata dal gas.
Svolgere i calcoli per R = 2 cm, m = 7 kg, T=120°C.
La trasformazione del gas è isobara alla pressione
p= p0+mg/R2 = 1.53 atm.
Mentre la temperatura finale è Tf= 420 K.
Allora Vf = RTf /p = 22.54 l
E calcolando la variazione di entropia su una isobara reversibile
S = cp ln(Vf/Vi) = 7 J/K
Esercizio n. 3 Una spira piana realizzata con due maglie quadrate di lati a e b
b
(vedi figura) è immersa in un campo uniforme B (t )  B0 sin( t ) . Detta  la
resistenza per unità di lunghezza del filo della spira determinare l’ampiezza della
corrente indotta nella spira.
Eseguire i calcoli per a= 20 cm, b= 10 cm, B0= 10 mT, = 102 rad/s, = 50 /m.
b
 B(t)
a
a

f ind  a 2  b 2
 dB
 a
dt
2

 b 2 B0 cos(t )
f ind
1

(a 2  b 2 ) B0  cos(t )
R
(4a  4b)
B (a  b)
i0  0
 0,5A.
4
i (t ) 