RELAZIONE SULLE CONICHE SVOLTA TRAMITE APPLET
Una conica è una particolare curva ottenuta dall’intersezione di un piano con un cono generato da
una retta che ruota attorno a un asse di rotazione. A secondo della posizione del piano rispetto al
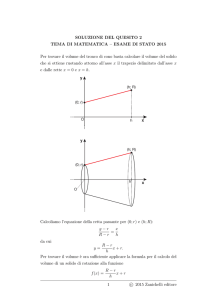
cono si originano differenti coniche. Nel primo applet possiamo osservare un cono di rotazione e un
piano che lo intersecano e possiamo osservare tre valori: y, θ e x. Al variare di y varia la posizione del
piano sull’asse delle ordinate muovendosi verso l’alto e verso il basso; al variare di θ varia
l’angolazione con cui il piano interseca il cono; e al variare di x si può spostare il piano a destra e a
sinistra. Variando questi valori possiamo ottenere diverse coniche. Variamo l’angolo del piano e
osserviamo cosa otteniamo: nell’intervallo che va da 0° a 4° otteniamo come parabola un cerchio,
nell’intervallo tra 5° e 43° otteniamo un ellisse, nell’intervallo tra 44° e 46° otteniamo una parabola, e
da 47° a 90° otteniamo un’iperbole. Da questo possiamo capire che quando il piano interseca il cono
perpendicolarmente si ottiene un cerchio, quando è secante rispetto al cono si ottiene un’iperbole,
quando è inclinato si ottiene un’ellisse, mentre quando il piano è parallelo a una delle rette
generatrici del cono.
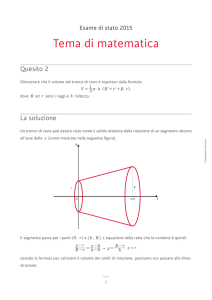
Ora tramite altre immagini illustriamo le coniche in 2D e 3D tramite un piano cartesiano ortogonale e
un modello 3D di un cono:
In questa immagine osserviamo nel modello 3D che il piano è perpendicolare al cono e osserviamo
nel piano cartesiano che otteniamo un cerchio.
In questa immagine osserviamo che il piano è inclinato rispetto al cono e nel piano cartesiano
osserviamo un’ellisse.
In questa terza immagine il piano è perpendicolare a un delle generatrici del cono, come osserviamo
nel modello 3D, mentre nel modello 2D vediamo che è presente una parabola.
In quest’ultima immagine vediamo che il piano rispetto al cono è secante ed è anche verificato, dal
piano cartesiano, che otteniamo un’iperbole.