Prova scritta di Fisica Generale I del 4 marzo 2011

Prova scritta di Fisica Generale I del 4 marzo 2011 – Ing. Gestionale Log e Prod COR-MA
I.1 Si consideri un punto materiale di massa m=100g,
viene lanciato dal punto O con velocità iniziale
v0=25.5m/s ed angolo di lancio . il punto passa per il
punto A distante R=50m dal punto di lancio, e va a
cadere nel punto P (v. figura, h=250m) Determinare (i)
l’angolo di lancio  e lo spostamento orizzontale d, e (ii)
il momento della quantità di moto del punto materiale
nell’istante in cui esso tocca il suolo in P rispetto al punto
di lancio O.
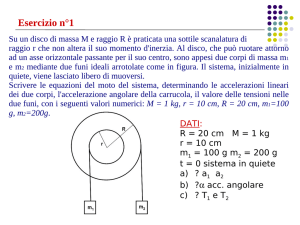
I.2 Si consideri il sistema di figura formato da M=1Kg e
m=100g. La superficie tra le due masse è scabra ed i
coefficienti di attrito statico e dinamico sono
rispettivamente 0.5 e 0.2. La forza F è applicata al corpo
M con un angolo =/10, mentre il piano su cui poggia M
è scabro (D=0.1). Determinare (i) il massimo valore di F
(Fmax) affinchè le due masse procedano insieme, e (ii)
l’accelerazione di M se la forza F applicata ha modulo
pari a 2Fmax con Fmax valutato al punto precedente.
V0

A
O
h
R
P
d
m
F

M
II.1 Si consideri un urto elastico tra due masse m1= 100g e m2 = 2m1. Dopo l’urto la particella m2 procede con velocità
V2=(5/3) metri/sec, mentre prima dell’urto la velocità del centro di massa valeva vCM= 4/3 metri/sec. Determinare (i) la
velocità della particella m1 prima dell’urto, (ii) l’impulso I1 che ha agito su m1 durante l’interazione con m2,e (iii) la velocità
di m2 rispetto al centro di massa prima dell’urto.
II.2 Due masse A e B di 3Kg e 4Kg rispettivamente sono collegate mediante un filo inestensibile e senza peso, che passa su
di una carrucola (disco) di massa M=2Kg e raggio R=10cm. Il filo non striscia sulla carrucola. La massa B è poggiata su di un
piano inclinato scabro (=/3, D=0.1). Determinare (i) l’accelerazione comune delle due masse, (ii) il tempo necessario alla
carrucola a compiere un giro se il sistema è inizialmente fermo.
Prova scritta di Fisica Generale II del 4 marzo 2011 – Ing. Gestionale Log e Prod COR-MA
I Si considerino i due segmenti carichi uniformemente
con =1nC/mm e di lunghezza L=10cm posti come in
Figura. Determinare (i) il valore del campo elettrico nel
punto O mostrato in figura (a=1cm), ed (ii) il momento
meccanico che agisce su di un dipolo elettrico
p=5nCm(i+ j) situato in O.

L/2
a

p
O a
L
L/2
II Si consideri un filo indefinito uniformemente carico (=1nC/m ) coassiale con un guscio cilindrico di raggio interno a=1cm
e raggio esterno b=2cm, riempito di materiale dielettrico (r=2.3). Determinare (i) il lavoro che un agente esterno deve
compiere per spostare una carica q0=1nC da un punto a distanza a/2 ad un punto a distanza 3b dall’asse del sistema, (ii) la
densità di carica di polarizzazione sulla superficie esterna del guscio cilindrico, (iii) (facoltativo) il potenziale elettrostatico
nel punto situato a distanza a/2 dal filo sapendo che V(r=3b)=0
III Si consideri una sbarretta di lunghezza L=1m, massa
M=1Kg e resistenza R=10ohm che, collegata a dei binari
di resistenza trascurabile, cade per effetto della gravità,
partendo da ferma, in una zona in cui agisce un campo
magnetico uniforme di intensità B=10T diretto
perpendicolarmente al piano del circuito come mostrato
in Figura. Determinare (i) la velocità della sbarretta dopo
un tempo , essendo  il tempo caratteristico del moto
della sbarretta, (ii) l’energia dissipata per effetto Joule
sulla sbarretta nello stesso intervallo di tempo.
IV Si consideri il circuito mostrato in Figura dove il valore
dell’intensità di corrente che aumenta con rapidità
=10mA/s partendo da I=0 a t=0. Determinare (i) il
campo di induzione magnetica B nel punto P in funzione
del tempo, assumendo a=10cm; (ii) l’intensità ed il verso
della corrente indotta in una spira circolare di raggio
R=100m e resistenza r=1 con centro in P dopo un
tempo t=10s.
x
x
x
x
x
x M, L
x
x
x
x
x
x
x
x
x
x
B
P
a
a
I
I