Corso di laurea: Scienze Geologiche
ESAME DI FISICA DEL 23/ 1/ 2008
ESERCIZIO 1
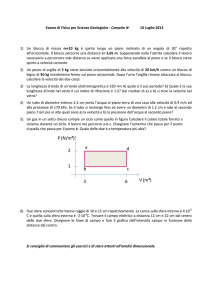
Un blocco di massa mB = 35 Kg (blocco B) è appoggiato su un piano orizzontale scabro ed è collegato tramite
un filo inestensibile di massa trascurabile ad un blocco di massa mA = 2.0 Kg (blocco A) e ad un solaio (vedi
Fig. 1). Il tratto di filo OB è orizzontale, il tratto OA è verticale e il tratto OC forma con la direzione verticale
un angolo = 30 (nota: nel punto O il filo non è fissato a nessun sostegno).
y
C
mB
O
B
Fig. 1
x
v0
A
m
mA
Il coefficiente di attrito statico tra blocco B e piano vale s = 0.12. Il sistema è in equilibrio statico.
1.1) Calcolare la forza di attrito statico Fa che agisce sul blocco B.
1.2) Calcolare la tensione del filo OC.
1.3) Calcolare m A max il valore massimo della massa del blocco A per cui il blocco B resta fermo.
Un proiettile di massa m = 10 g colpisce il blocco A con velocità v0 = 5.0 m/s nella direzione orizzontale
v0 v0 xˆ con un urto completamente anelastico.
1.4) Calcolare la velocità dopo l’urto e la tensione TA' del tratto di filo verticale OA un istante dopo l’urto,
sapendo che il tratto di filo OA è lungo L = 30 cm.
ESERCIZIO 2
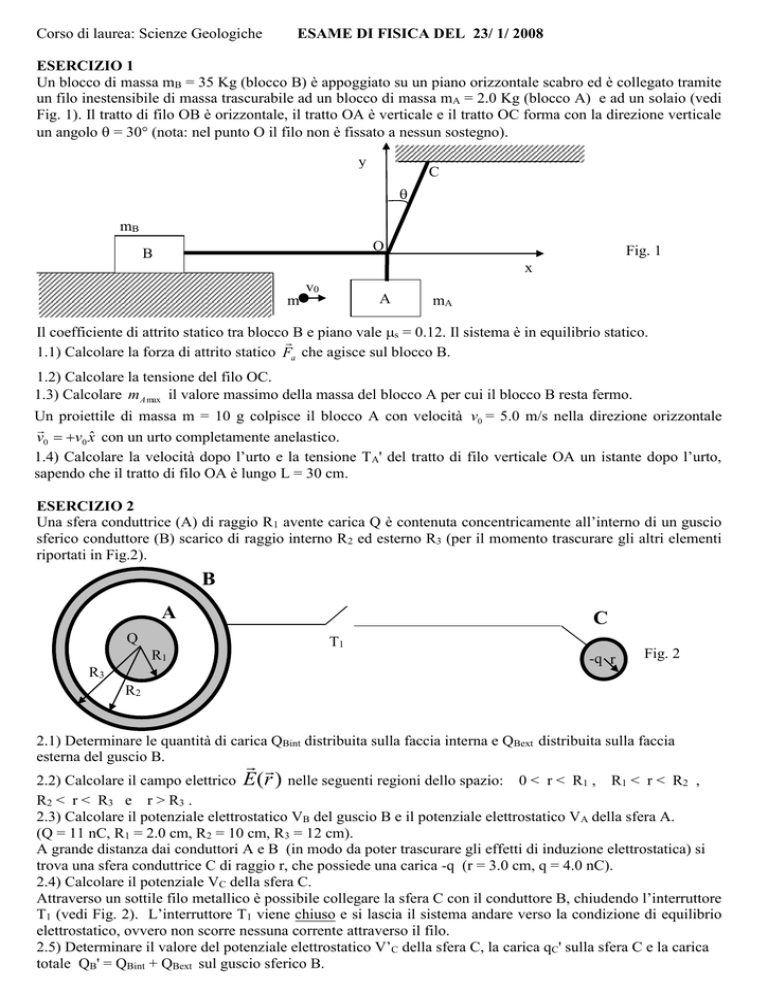
Una sfera conduttrice (A) di raggio R1 avente carica Q è contenuta concentricamente all’interno di un guscio
sferico conduttore (B) scarico di raggio interno R2 ed esterno R3 (per il momento trascurare gli altri elementi
riportati in Fig.2).
B
A
Q
C
T1
R1
-q r
R3
Fig. 2
R2
2.1) Determinare le quantità di carica QBint distribuita sulla faccia interna e QBext distribuita sulla faccia
esterna del guscio B.
E (r ) nelle seguenti regioni dello spazio:
2.2) Calcolare il campo elettrico
0 < r < R1 , R 1 < r < R2 ,
R2 < r < R 3 e r > R3 .
2.3) Calcolare il potenziale elettrostatico VB del guscio B e il potenziale elettrostatico VA della sfera A.
(Q = 11 nC, R1 = 2.0 cm, R2 = 10 cm, R3 = 12 cm).
A grande distanza dai conduttori A e B (in modo da poter trascurare gli effetti di induzione elettrostatica) si
trova una sfera conduttrice C di raggio r, che possiede una carica -q (r = 3.0 cm, q = 4.0 nC).
2.4) Calcolare il potenziale VC della sfera C.
Attraverso un sottile filo metallico è possibile collegare la sfera C con il conduttore B, chiudendo l’interruttore
T1 (vedi Fig. 2). L’interruttore T1 viene chiuso e si lascia il sistema andare verso la condizione di equilibrio
elettrostatico, ovvero non scorre nessuna corrente attraverso il filo.
2.5) Determinare il valore del potenziale elettrostatico V’C della sfera C, la carica qC' sulla sfera C e la carica
totale QB' = QBint + QBext sul guscio sferico B.