Fisica Sperimentale II – Ottica e Optometria

Fisica Sperimentale II – Ottica e Optometria
I compitino – 25 Ottobre 2012
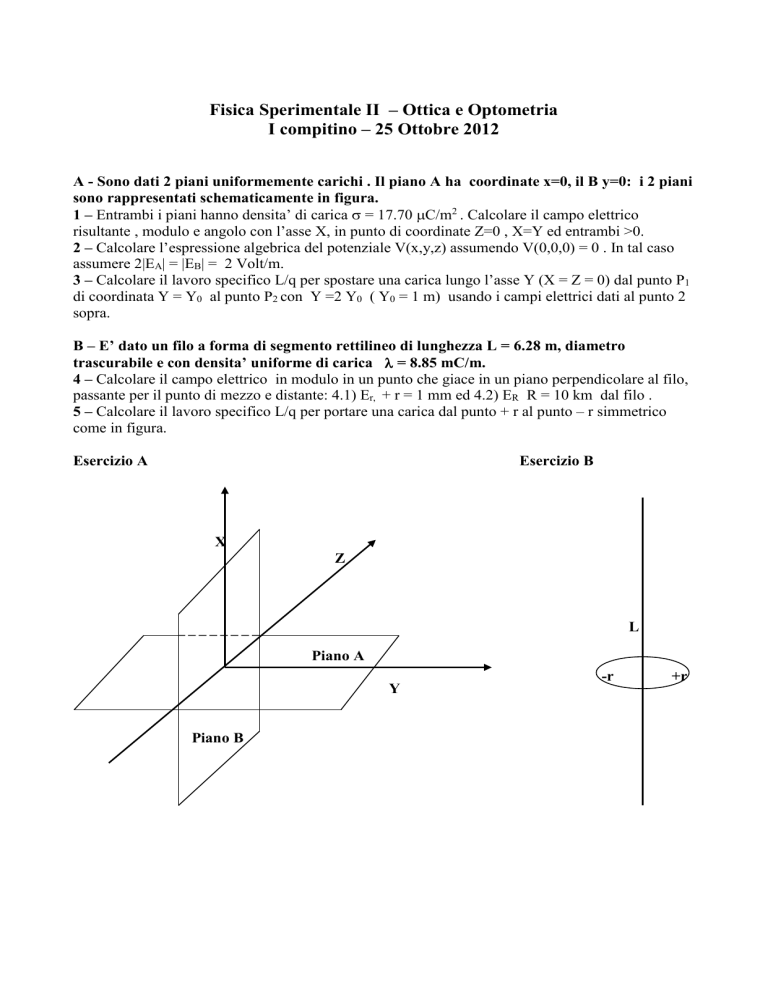
A - Sono dati 2 piani uniformemente carichi . Il piano A ha coordinate x=0, il B y=0: i 2 piani
sono rappresentati schematicamente in figura.
1 – Entrambi i piani hanno densita’ di carica  = 17.70 C/m2 . Calcolare il campo elettrico
risultante , modulo e angolo con l’asse X, in punto di coordinate Z=0 , X=Y ed entrambi >0.
2 – Calcolare l’espressione algebrica del potenziale V(x,y,z) assumendo V(0,0,0) = 0 . In tal caso
assumere 2|EA| = |EB| = 2 Volt/m.
3 – Calcolare il lavoro specifico L/q per spostare una carica lungo l’asse Y (X = Z = 0) dal punto P1
di coordinata Y = Y0 al punto P2 con Y =2 Y0 ( Y0 = 1 m) usando i campi elettrici dati al punto 2
sopra.
B – E’ dato un filo a forma di segmento rettilineo di lunghezza L = 6.28 m, diametro
trascurabile e con densita’ uniforme di carica = 8.85 mC/m.
4 – Calcolare il campo elettrico in modulo in un punto che giace in un piano perpendicolare al filo,
passante per il punto di mezzo e distante: 4.1) Er, + r = 1 mm ed 4.2) ER R = 10 km dal filo .
5 – Calcolare il lavoro specifico L/q per portare una carica dal punto + r al punto – r simmetrico
come in figura.
Esercizio A
Esercizio B
X
Z
L
Piano A
Y
Piano B
-r
+r
Fisica Sperimentale II – Ottica e Optometria
I compitino – 25 Ottobre 2012
Risoluzione
1 – Entrambi i piani producono campi elettrici costanti uguali E = ed ortogonali fra loro. Il
campo risultante sara’ dato dal teorema di Pitagora:

17.7 *10 6
2
2
Etot  E  E = E √2 =
2=
2 = 10 +6 * 1.414 V/m e quindi costante in
12
2 0
2 * 8.85 *10
tutti punti.
Essendo le due componenti uguali e perpendicolari fra loro sara’ 45 gradi.
2 – V(x,y,z) = - EA *x –EB * y = (- 1x-2y) Volt. (n.b. x e y in metri)
3 – L/q = V(P1) – V(P2) = - 2 Y0 - (-2 *2 Y0) = 2 Y0 = 2 Joule/C = 2 Volt.
4–
4.1 - Per r = 1 mm si puo’ usare il teorema di Gauss essendo r << L

8.85 *10 3
quindi Er =
=
= 0.159 * 10+12 V/m
20 r
2 8.85 *10 12 *10 3
4.2 - Per R = 10 km il segmento e’ visto come se fosse una carica puntiforme Q = L
L
8.85 *10 3 * 6.28
quindi ER =
=
= 0.5 * 10+1 V/m
2
12
8
40 R
4 8.85 *10 *10
5 – L/q = 0 . Muovendosi per es. lungo la circonferenza indicata in figura il campo E e’ sempre
perpendicolare allo spostamento quindi il lavoro, che e’ indipendente dal percorso fatto dato che il
campo e.s. e’ conservativo, e’ nullo.