funzioni in 2 variabili

INTEGRALI DEFINITI
D
DE
EF
FIIN
NIIZ
ZIIO
ON
NE
E::
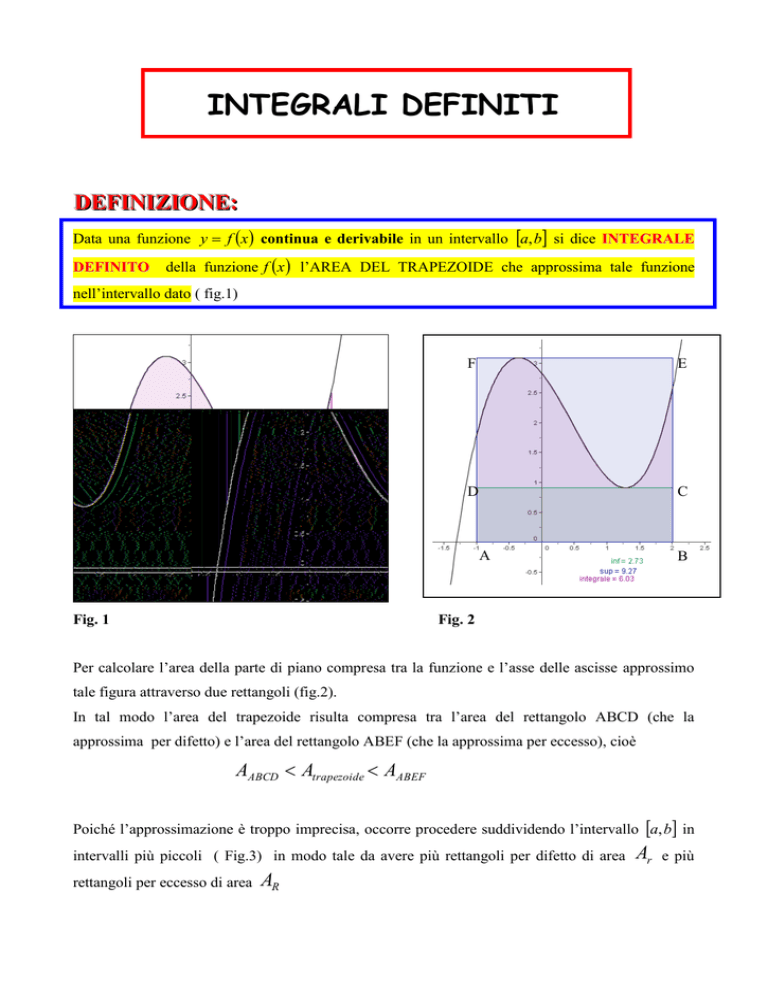
Data una funzione y  f x  continua e derivabile in un intervallo a, b si dice INTEGRALE
DEFINITO
della funzione f x  l’AREA DEL TRAPEZOIDE che approssima tale funzione
nell’intervallo dato ( fig.1)
F
E
D
C
A
Fig. 1
B
Fig. 2
Per calcolare l’area della parte di piano compresa tra la funzione e l’asse delle ascisse approssimo
tale figura attraverso due rettangoli (fig.2).
In tal modo l’area del trapezoide risulta compresa tra l’area del rettangolo ABCD (che la
approssima per difetto) e l’area del rettangolo ABEF (che la approssima per eccesso), cioè
AABCD  Atrapezoide  AABEF
Poiché l’approssimazione è troppo imprecisa, occorre procedere suddividendo l’intervallo a, b in
intervalli più piccoli ( Fig.3) in modo tale da avere più rettangoli per difetto di area
rettangoli per eccesso di area
AR
Ar
e più
Dividendo l’intervallo a, b in
quando
n
intervalli,
n 
la somma delle aree degli n rettangoli rn
che approssimano la funzione per difetto
diventa sempre più corrispondente alla somma
delle aree degli n rettangoli Rn che la
approssimano per eccesso, e quasi uguale
all’area del trapezoide, cioè

A
n 1
se
lim
n
A
rn
 lim
n 
A
Rn
l
dove con
l
rn

 Atrapezoide   ARn
n 1
si indica il valore di tale limite
allora si dice che l
è il valore dell’ INTEGRALE DEFINITO della funzione f x 
nell’intervallo a, b ed esso corrisponde proprio all’ AREA DELLA PARTE DI PIANO
COMPRESA TRA LA FUNZIONE E L’ASSE DELLE ASCISSE
PER CAPIRE MEGLIO
consulta il sito
http://fds.mate.polimi.it/file/4/File/freesoftware/integrale3.html
aprendolo con CTRL + CLIC sul link
C
CA
AL
LC
CO
OL
LO
OD
DE
EL
LL
L’’IIN
NT
TE
EG
GR
RA
AL
LE
ED
DE
EF
FIIN
NIIT
TO
O
T
TE
EO
OR
RE
EM
MA
AD
DII T
TO
OR
RR
RIIC
CE
EL
LL
LII –– B
BA
AR
RR
RO
OW
W
Data una funzione y  f x  continua e derivabile in un intervallo a, b per calcolare l’integrale
definito si usa la formula seguente
b
 f ( x)dx  F (b)  F (a)
a
dove con
F x  si indica la generica funzione primitiva di f x 
Quindi per calcolare l’integrale definito in un intervallo a, b dato, si deve seguire il seguente
procedimento:
1. calcolo l’insieme delle generiche funz. primitive
F x 
2. calcolo il valore che tale funz. primitiva assume in
b , cioè F b 
3. calcolo il valore che tale funz. primitiva assume in
a , cioè F a 
4. calcolo la differenza
N
N..B
B..
F b  F (a)
OTTENGO COME RISULTATO non più una funzione ma UN NUMERO
ESEMPIO:
3
 x2

9  5


x

3
dx


3
x


     2
2

1
2
 2

1
3
F (b)  F (3) 
32
 33 
9
2
2
1
5
F (a )  F (1)   3  
2
2
9  
9
2
P
PR
RO
OP
PR
RIIE
ET
TA
A’’ D
DE
EG
GL
LII IIN
NT
TE
EG
GR
RA
AL
LII D
DE
EF
FIIN
NIIT
TII
DIMOSTRAZIONE
a
a
 f ( x)dx  0
1.
 f ( x)dx  F (a)  F (a)  0
a
a
b
a
a
b
 f ( x)dx   f ( x)dx
2.
DIMOSTRAZIONE
b
Sapendo che
a
 f ( x)dx  F (b)  F (a)
e
a
 f ( x)dx  F (a)  F (b)
b
Si può calcolare
a
b
b
a
  f ( x)dx  [ F (a)  F (b)]   F (a)  F (b)  F (b)  F (a)   f ( x)dx
3.
c
b
b
a
c
a
 f ( x)dx   f ( x)dx   f ( x)dx
DIMOSTRAZIONE
c
 f ( x)dx  F (c)  F (a)
a
b
e
 f ( x)dx  F (b)  F (c)
c
quindi
c
b
b
a
c
a
 f ( x)dx   f ( x)dx  [ F (c)  F (a)]  [ F (b)  F (c)]  F (b)  F (a)   f ( x)dx