UN APPROCCIO FEM NEURALE PER LA UNBOUNDED MAGNETIC
FIELD ANALYSIS IN PRESENZA DI MATERIALI CON ISTERESI
S. Coco1, A. Laudani1, F. Riganti Fulginei2 and A. Salvini2
1
2
DIEES, Università di Catania, V.le A. Doria 6, Catania I-95125, Italia
DEA, Università Roma Tre, Via della Vasca Navale, 84, Roma I-00146, Italia
In questa memoria viene presentato un algoritmo che sfrutta una sinergia [1] tra il metodo
degli elementi finiti (FEM) [2] e le reti neurali artificiali (NNs) [3] per l’analisi di problemi
magnetici nei materiali a comportamento isteretico spazialmente illimitati. Partendo dalla
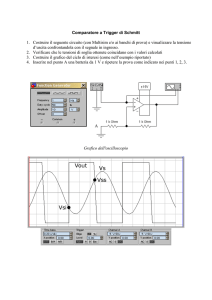
misura di un esiguo numero di cicli di isteresi asimmetrici saturi (Fig 1) è possibile costituire
un set di pattern di addestramento sul quale addestrare un’opportuna rete neurale artificale
costituita da 2 ingressi (il campo magnetico H e la densità di flusso B), 9 neuroni nell’unico
strato nascosto ed un’uscita il cui valore è pari alla permeabilità magnetica
differenzuale d ( H , B) dB / dH .
Fig. 1. Esempio cicli di isteresi saturi ed asimmetrici utilizzabili come set di pattern di addestramento per la NN
(M indica il tratto di curva del ciclo maggiore mentre A indica il tratto di curva del ciclo asimmetrico).
In questo modo, attraverso l’utilizzo della tecnica di transplantation [4] e sfruttando la
simmetria del problema la rete neurale artificiale è in grado di simulare, oltre al ciclo
maggiore, anche tutti i cicli di isteresi minori simmetrici (saturi e non saturi) e tutti i cicli di
isteresi asimmetrici (saturi e non saturi). La tecnica di transplantation viene utilizzata solo per
per i cicli minori che risultano essere sia asimmetrici sia non saturi, mentre i tratti di curva
della Fig. 1 indicati con la lettera A possono essere sfruttati per generare tutti i cicli minori
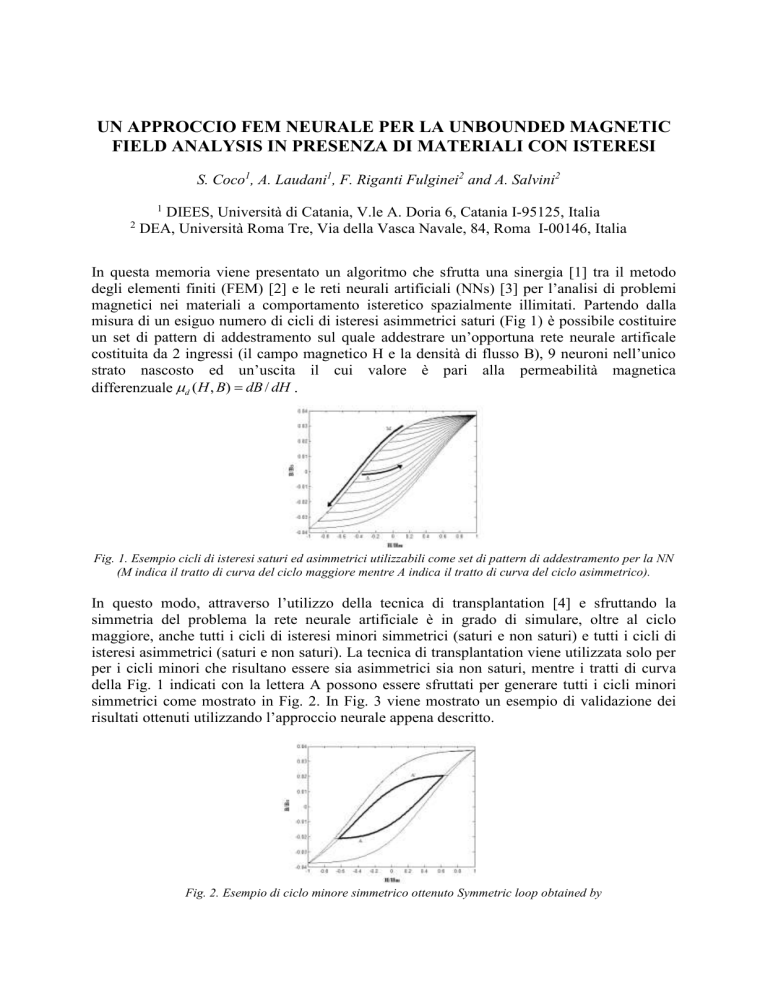
simmetrici come mostrato in Fig. 2. In Fig. 3 viene mostrato un esempio di validazione dei
risultati ottenuti utilizzando l’approccio neurale appena descritto.
Fig. 2. Esempio di ciclo minore simmetrico ottenuto Symmetric loop obtained by
the superposition of mirror asymmetric branches
Fig. 3. Esempio di validazione dei risultati ottenuti con la rete neurale
A questo punto, sfruttando la capacità predittiva della rete neurale è possibile ottenere i valori
di campo desiderati in corrispondenza dei punti di una apposita mesh generata per
approssimare il problema magnetico con tecnica FEM. Di seguito viene riportato un esempio
di applicazione su di un cilindro ferromagnetico di 8 cm di lunghezza e 1 cm di raggio
avvolto in un solenoide percorso da una corrente uniforme di 1 A. Come è noto, partendo
dalle equazioni di Maxwell è possibile ottenere l’equazione:
1
A J M
0
(1)
(dove 0 è la permeabilità magnetica nel vuoto, J il vettore densità di corrente ed M la
magnetizzazione) da cui è sato ricavato il potenziale vettore A (Fig. 4).
Fig. 4. Intensità del potenziale vettore A dell’equazione (1) per l’esempio considerato
Bibliografia
[1] F.R. Fulginei and A. Salvini, “Softcomputing for the Identification of the Jiles–Atherton
Model Parameters”, IEEE Trans. On Magnetics, vol. 41, n. 3: 1100-1108, March 2005.
[2] S. Coco and A. Laudani, “Iterative FE Solution of Unbounded Magneto-Thermal
Problems”, 10th IGTE Symposium on Numerical Field Calculation in Electrical
Engineering, Sept 16-18, 2002 Graz, Austria.
[3] C. Serpico and C. Visone, “Magnetic Hysteresis via Feed-Forward Neural Networks”,
IEEE Trans. On Magnetics, vol. 34, no. 3: 623-628, May 1998.
[4] E. Zirka and Y. I. Moroz, “Hysteresis modeling based on transplantation,” IEEE Trans. on
Mag., vol. 31, no. 6, pp. 3509–3511, Nov. 1995.