LICEO SCIENTIFICO STATALE
“GIORDANO BRUNO”
Via Gino Marinuzzi, 1 10156 TORINO
tel 011 2624884 / fax 011 2621682
e-mail: [email protected]
www.gbruno.it
PIANO DI LAVORO
Anno Scolastico 2010-2011
DOCENTE
DISCIPLINA
CLASSE
BROZZETTI Eliana
MATEMATICA
1^
SEZ
BL
1. SITUAZIONE DI PARTENZA DELLA CLASSE
Numero alunni
Clima educativo della
classe
(problematico,
accettabile, buono,
ottimo)
23
accettabile
Livello cognitivo
globale di ingresso
(problematico,
accettabile, buono,
ottimo)
Svolgimento del
programma
precedente
(incompleto,
regolare, anticipato)
accettabile
/
2. OBIETTIVI
I docenti del consiglio di classe della 1^BL, nell’ambito delle competenze chiave di cittadinanza,
hanno deciso di lavorare in modo prioritario su:
- Imparare ad imparare
- Collaborare e partecipare
Per sviluppare dette competenze si lavorerà sui seguenti obiettivi trasversali:
Obiettivi educativi:
1. acquisire un comportamento corretto e responsabile nei confronti dei compagni, dei
docenti e del personale scolastico
2. essere disponibili ad interagire con i compagni attraverso un atteggiamento
improntato alla tolleranza e allo spirito di collaborazione
3. rispettare le scadenze e la puntualità nell’esecuzione dei compiti assegnati
4. rispettare e utilizzare responsabilmente le strutture e i beni dell’Istituto
5. Accettare e valorizzare le diversità
Obiettivi didattici:
1. potenziare e affinare il metodo di studio
2. acquisire la capacità di organizzare in modo autonomo il lavoro scolastico
3. sviluppare le capacità di ascolto, di lettura, di analisi e di sintesi
4. sviluppare e affinare le capacità di osservazione e di percezione spazio-temporale
5. acquisire la capacità di esprimersi in modo chiaro, corretto ed appropriato nel
linguaggio tipico di ogni disciplina
Nel dipartimento di Matematica e Fisica, per il biennio, sono stati concordati i seguenti
OBIETTIVI DISCIPLINARI TRASVERSALI DI MATEMATICA
Lo studente dovrà:
Sapersi esprimere con proprietà di linguaggio, utilizzando termini specifici della materia;
Acquisire disinvoltura nel calcolo numerico e, soprattutto, nel calcolo letterale;
Saper risolvere problemi algebrici, geometrici e logici, matematizzando semplici situazioni
problematiche;
Aver chiaro cosa si intende per assioma e teorema; saper dimostrare, rendendosi conto
dell’importanza del motivare i procedimenti risolutivi;
Contestualizzare storicamente alcuni momenti fondamentali del pensiero matematico;
Acquisire la capacità di leggere e interpretare un testo matematico-scientifico;
Saper cogliere le attinenze della matematica sia con situazioni reali, sia con le altre discipline:
Acquisire capacità di analisi e di sintesi, sviluppando il ragionamento deduttivo e induttivo.
OBIETTIVI DISCIPLINARI SPECIFICI
far acquisire allo studente: la conoscenza di tecniche e procedure di calcolo (numerico e
algebrico); la capacità di utilizzarle consapevolmente per la risoluzione di esercizi e
problemi.
far acquisire allo studente: la conoscenza delle principali proprietà geometriche del piano
euclideo; la capacità di utilizzarle per dimostrare teoremi e problemi
MONTE ORE ANNUALE PREVISTO DAL CURRICOLO NELLA CLASSE: 99 ore
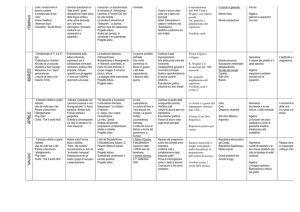
3. CONTENUTI organizzazione dei contenuti disciplinari esposti per
x Moduli
e/o
x Unità tematiche e didattiche
Percorsi formativi ed eventuali approfondimenti
Contenuti
e/o
Periodo
ALGEBRA:
i numeri (naturali, interi relativi, razionali) e operazioni con essi.
Calcolo letterale: monomi
GEOMETRIA:
1°
quadrimestre
introduzione alla geometria euclidea del piano
INFORMATICA: introduzione a Derive e suo utilizzo per la risoluzione di
esercizi inerenti al programma di algebra; Cabrì (Versione Geogebra) per
esercitazioni inerenti al programma di geometria
ALGEBRA:
2°
quadrimestre
calcolo letterale: polinomi, prodotti notevoli
scomposizione dei polinomi in fattori
frazioni algebriche
GEOMETRIA:
I triangoli (criteri di congruenza)
INFORMATICA:
utilizzo di Derive per la risoluzione di esercizi inerenti al programma di algebra
Utilizzo di Geogebra
STATISTICA descrittiva: concetti fondamentali; frequenze e tabelle;
rappresentazioni grafiche dei dati; valori di sintesi.
4. PROGRAMMAZIONE ATTIVITA’ EXTRACURRICOLARI (laboratori, visite
guidate, conferenze, spettacoli teatrali o cinematografici, ecc.)
Olimpiadi di matematica (Giochi di Archimede: in Istituto 17 novembre 2010)
Stage di matematica (3 giorni) a Bardonecchia, per gli studenti eccellenti
Progetto Diderot ”MATE-TRAINING” per il biennio, della Fondazione CRT
Corso sul metodo di studio: “Imparo ad imparare”
5. METODOLOGIE UTILIZZATE
x Lezione frontale
x Esercitazione di laboratorio
x Gruppi di lavoro
x Approfondimento individuale
x Discussione guidata
x Utilizzo di Internet
Approccio pluridisciplinare
Utilizzo materiale audiovisivo e/o multimediale
x Attività di recupero
altro
6. MEZZI
x Testo in adozione
x schede
x Strumenti multimediali
Riviste/giornali
altro
x appunti
7. SPAZI
X aula
x laboratori
biblioteca
palestre
Viaggio d’istruzione, scambi culturali, approfondimenti
linguistici
Mostre, spettacoli
Visite guidate
x stage
8. NUMERO E TIPOLOGIA DELLE VERIFICHE IMPIEGATE
Numero di verifiche previste a quadrimestre
SCRITTE
ORALI
0
Almeno 3
Tipologia:
x prove strutturate
x prove semistrutturate
prove pratiche individuali o di gruppo
x prove orali individuali (o di gruppo)
relazioni individuali o di gruppo
x prove scritte o grafiche
prove al computer
controllo di quaderni e/o di elaborati
9. CRITERI DI VALUTAZIONE (anche in riferimento alle decisioni del proprio
Dipartimento)
In entrambi i quadrimestri è stato concordato, a livello dipartimentale, che il voto finale sia unico
(orale). La valutazione dell’apprendimento e dello studio individuale si effettuerà mediante
interrogazioni orali, alcune delle quali sostituibili con test e/o verifiche scritte, articolate su domande
teoriche e risoluzione di esercizi.
Le verifiche scritte saranno articolate in modo da presentare le difficoltà in ordine crescente,
riguarderanno l’applicazione delle nozioni acquisite durante lo svolgimento delle lezioni.
Le verifiche orali (anche sostituibili con test scritti) mireranno ad accertare anche l’acquisizione del
linguaggio matematico oltre che l’autonomia nei ragionamenti e nell’applicazione dei principi
matematici.
Per l’assegnazione del voto ci si attiene ai criteri generali di valutazione indicati nel P.O.F.
Gli alunni assenti alle lezioni sono tenuti ad informarsi sugli argomenti trattati in classe ed
impegnarsi nella loro comprensione, l’insegnante fornirà spiegazioni in classe su domande
specifiche.
In caso di assenza durante una verifica scritta l’alunno recupererà una analoga prova al suo rientro
dall’assenza o successivamente.
La valutazione sommativa finale di ogni alunno, terrà conto non solo del livello raggiunto nella
disciplina, ma anche dei seguenti parametri:
-
autonomia di studio;
livello di partenza;
impegno;
interesse e partecipazione;
rispetto degli impegni concordati.
Al fine della promozione, è necessario avere una conoscenza almeno sufficiente di quasi tutti i
contenuti del programma, non solo di quelli del secondo quadrimestre.
Data 30 ottobre 2010
Firma del docente _
Eliana Brozzetti