Eesercizio 1
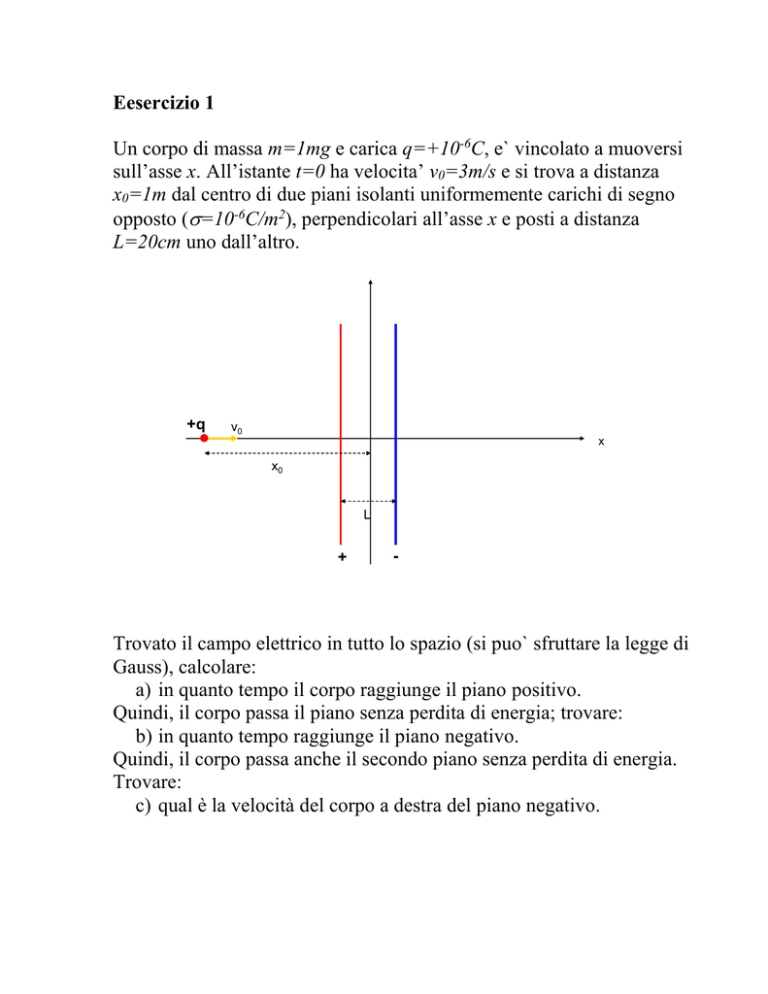
Un corpo di massa m=1mg e carica q=+10-6C, e` vincolato a muoversi
sull’asse x. All’istante t=0 ha velocita’ v0=3m/s e si trova a distanza
x0=1m dal centro di due piani isolanti uniformemente carichi di segno
opposto (=10-6C/m2), perpendicolari all’asse x e posti a distanza
L=20cm uno dall’altro.
+q
v0
x
x0
L
+
-
Trovato il campo elettrico in tutto lo spazio (si puo` sfruttare la legge di
Gauss), calcolare:
a) in quanto tempo il corpo raggiunge il piano positivo.
Quindi, il corpo passa il piano senza perdita di energia; trovare:
b) in quanto tempo raggiunge il piano negativo.
Quindi, il corpo passa anche il secondo piano senza perdita di energia.
Trovare:
c) qual è la velocità del corpo a destra del piano negativo.
Soluzione dell’esercizio 1
Il campo elettrico è nullo a sinistra del piano positivo e a destra del
piano negativo. Tra i due piani il campo vale
10 6
V
E
1.13 105
12
0 8.85 10
m
ed è diretto perpendicolarmente ai piani, con verso da sinistra a destra.
Il corpo non risente di forza elettrica a sinistra del piano positivo e a
destra del piano negativo. Tra i due piani risente di una forza costante,
diretta verso destra.
a) Il tempo impiegato per raggiungere il piano positivo è
semplicemente
t
x0 L 2 1 0.1
0.3s
v0
3
b) Il tempo per raggiungere il piano negativo si trova osservando che il
moto è ora uniformemente accelerato, con accelerazione
F qE 106 1.13 105
a
1.13 105 m / s 2
6
m m
10
Applicando la formula del moto accelerato:
L v0 t
1 2
at
2
E risolvendo per t:
3
2 0.2
3
v 2 L v0
t 0
5
5
5
a
a
1.13 10 1.13 10 1.13 10
a
2
2
7.05 10 10 3.54 10 6 2.65 10 5 1.85 10 3 s
c) Per trovare la velocità finale possiamo applicare il teorema
dell’energia cinetica:
K f Ki W
Ove W e` il lavoro compiuto dalla forza elettrica
1 2 1 2
mv f mv0 qEL
2
2
Da cui
2qEL
2 10 6 1.13 105 0.2
2
v f v0
3
213m / s
m
106
2
Esercizio 2
Quattro fili indefiniti, percorsi nello stesso verso dalla stessa corrente
I=10A, sono posti sugli spigoli di un parallelepipedo a sezione
quadrata, di lato a=1cm.
1
a
2
1
3
4
C
D
3
4
3
Con riferimento ad una sezione, trovare intensità, direzione e verso del
campo magnetico
a) nel punto C, centro della sezione;
b) nel punto D, centro del segmento tra i fili 3 e 4.
Trovata l’espressione approssimata del campo magnetico in funzione
della distanza r tra il punto C e un punto della sezione a distanza molto
maggiore di a, trovare
c) il campo magnetico per r=100 a.
Soluzione dell’esercizio 2
Il campo risultante è la somma dei campi generati dai quattro fili.
a) Nel punto C tutti i 4 campi sono uguali in modulo, ma la loro somma
è, vettorialmente, zero, in quanto ogni coppia di fili opposti dà un
contributo uguale e contrario (regola della mano destra).
b) Nel punto D il campo totale si riduce alla somma dei campi dovuti ai
fili 1 e 2, poiché gli altri due fili danno contributi uguali e contrari.
I
I
B B1 B2 0 vˆ1 0 vˆ2
2 r1
2 r2
Il vettore r1 congiunge il filo 1 al punto D, il versore v1 è
perpendicolare a questo vettore, con verso determinato dalla regola
della mano destra. Similmente sono definiti r2 e v2.
2
5
a
r1 r2 r a
a
2
2
a
2
cos
r
5
2
B2
1
r1
a
B1
D
r2
2
Il modulo del campo risultante vale:
4
B
0 I
I
2
2 cos 0
2
2 r
2 a 5 2
5
2 10 7
8 10
3.20 10 4 T
2
5 10
La direzione e` data dal segmento che congiunge i fili 3 e 4, il verso e`
da 3 a 4.
In un punto molto distante da C, si puo` trascurare la distanza a tra i fili
e immaginare che esista un unico filo che porta la somma (algebrica)
delle quattro correnti. Il campo è approssimatamene dato da:
B
c) Per r=100 a, vale:
B
0 4I
2 r
0 4I
4 10
2 10 7
8.00 10 6 T
2
2 r
100 10
Esercizio 3
Un solenoide indefinito di raggio R=10cm, ha n=10 spire/cm ed è
percorso da una corrente I=10A. Trovare:
a) il campo magnetico all’interno del solenoide (si puo` fare uso
della legge di Ampère);
b) la densità di energia magnetica dentro il solenoide;
c) l’energia magnetica contenuta in uno spicchio del solenoide di
ampiezza angolare =15° e lunghezza L=1m;
d) quanto vale la densità di energia magnetica al di fuori del
solenoide? Giustificare la risposta.
L
R
Soluzione dell’esercizio 3
a) Il campo B all’interno del solenoide vale:
B 0 nI 4 10 7 10 3 10 1.26 10 2 T
b) La densità di energia è:
um
1
2 0
B2
1
0 n 2 I 2
2
1
4 10 7 10 6 10 2 6.28 101 J / m 3
2
c) Poiché la densità di energia è costante, l’energia magnetica
immagazzinata nello spicchio è semplicemente il prodotto tra la densità
di energia e il volume:
1
U m u mV u m R 2 L
2
1
6.28 101
0.12 1 8.22 10 2 J
2 12
d) La densità di energia fuori dal solenoide è nulla, poiché qui il campo
magnetico è nullo.
Esercizio 4
Sia dato il seguente circuito, formato da tre resistenze, una fem
variabile E1 ed una fem fissa E2.
E1
1
R1
E2
A
2
R2
B
R3
Siano I1, I2, I3 le correnti che scorrono rispettivamente in R1, R2, R3.
Trovare l’espressione delle correnti mediante le leggi di Kirchhoff.
Dati i seguenti valori dei parametri R1=5, R2=10, R3=20, E2=2V,
trovare:
a) il valore della corrente I1 quando E1=2.5V;
b) il valore di E1 per cui la corrente I2 è nulla;
c) il valore di E1 per cui la corrente I3 è nulla. Commentare il segno
relativo tra E1 e E2;
d) la ddp tra A e B quando E1=4V.
Soluzione dell’esercizio 4
Applicando le leggi di Kirchhoff alle due maglie evidenziate nello
schema. Poniamo il verso convenzionale delle correnti come segue: I1
e I2 da destra a sinistra, I3 da sinistra a destra. Troviamo il sistema:
E1 E 2 I 1 R1 I 2 R2
E 2 I 1 R3 I 2 R2 R3
I 3 I1 I 2
Da cui, risolvendo per le correnti:
E1 R2 R3 E 2 R3
I1
R1 R2 R2 R3 R3 R1
I2
E 2 R3 R1 E1 R3
R1 R2 R2 R3 R3 R1
I3
E1 R2 E 2 R1
R1 R2 R2 R3 R3 R1
a) Per i valori assegnati dei parametri, otteniamo:
I1
2.5 30 2 20
100mA
5 10 10 20 20 5
b) Dall’espressione di I2, troviamo il valore di E1 cercato:
E1 E2
R1 R3
5 20
2
2.50V
R3
20
c) E analogamente per I3:
E1 E2
R1
5
2 1.00V
R2
10
Il segno negativo significa che i poli di E1 vanno scambiati per avere
nel ramo 3 una corrente contrapposta a quella generata da E2.
d) La ddp tra A e B si trova applicando la legge di Kirchhoff al ramo 3:
V A VB I 3 R3
E1 R2 E 2 R1
R3
R1 R2 R2 R3 R3 R1
10 4 5 2
20 2.86V
350












