I test di verifica per gli studenti

Progetto
"Matematica & Computer "
III Fase - Prima annualità del triennio della scuola secondaria superiore
a.s. 2001/2002
Modulo MatCos 1.6
(Febbraio
Studente __________________________
1° Test
(Gennaio 2002)
Cognome
Classe
1°
Nome
_________ Sezione _________
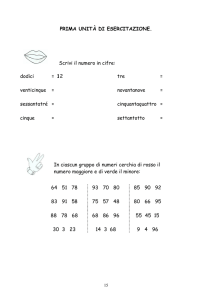
Dati i punti A (3, - 4) e M (1,1) si scriva un programma che:
a)
Calcoli e stampi le coordinate del II estremo del segmento che ha nel punto A il I
estremo e in M il punto medio;
b)
Disegni il segmento AB.
………………………………………………………………………………………….
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………..
Giudizio
2°
I
S
B
ND 
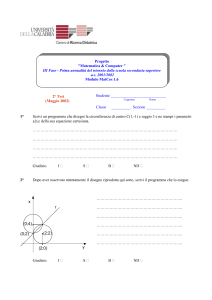
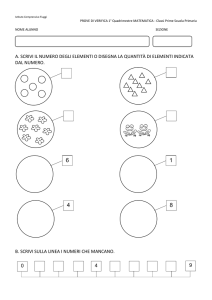
Dopo aver osservato attentamente il disegno riprodotto qui sotto, scrivi il programma che lo
esegue.
y
……………………………………………..
4
……………………………………………..
……………………………………………..
O
4
x
………………………………………………
………………………………………………
1
Giudizio
3°
I
S
B
ND 
Scrivi il programma che verifica se il quadrilatero di vertici A4,3 , B7,5 , C 5,8 , e
D2,6 è un rombo. Si può stabilire se è anche un quadrato? (motiva la risposta)
………………………………………………………………………………………….
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………..
Giudizio
4°
I
S
B
ND 
Siano A(2,3), B(1,-1), scrivi un programma che calcoli e stampi le coordinate di un qualsiasi
punto equidistante dagli estremi del segmento AB.
………………………………………………………………………………………….
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………..
Giudizio
5°
I
S
B
ND 
Scrivi un programma che disegni la retta di coefficiente angolare m=1/2 e intercetta q=3/4;
………………………………………………………………………………………….
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………..
Giudizio
6°
I
S
B
ND 
Scrivi un programma che tracci il grafico della funzione y  x  2 x  3 e dedurre se è
iniettiva.
3
2
………………………………………………………………………………………….
………………………………………………………………………………………….
2
………………………………………………………………………………………….
…………………………………………………………………………………………..
Giudizio
7°
I
S
B
ND 
Data la retta di equazione r : 2 x  y  1  0 , scrivi un programma che stampi le coordinate di
5 punti presi a caso su r ; verifica inoltre che dette coordinate soddisfano l’equazione data.
………………………………………………………………………………………….
………………………………………………………………………………………….
………………………………………………………………………………………….
…………………………………………………………………………………………..
Giudizio
8°
I
S
B
ND 
Descrivi “passo-passo” cosa esegue il seguente programma. Alla fine formula un enunciato
che contenga le tue considerazioni.
Rifcart;
colore(9);
f = funzione(“2*x +3”);
graficofunz(f);
colore(13)
g = funzione(“-1/2*x +5”);
graficofunz(g);
m = 2;
m1 =-1/2;
Se m*m1 =-1 allora
Stampa (“le due rette sono perpendicolari”);
altrimenti
stampa (“le due rette non sono perpendicolari”);
………………………………..
………………………………..
………………………………..
…………………………………
…………………………………
…………………………………
…………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
Giudizio
I
S
B
3
ND 
Descrivi “passo-passo” cosa esegue il seguente programma. Alla fine formula un enunciato
che contenga le tue considerazioni.
9°
Rifcart;
f = funzione(“3*x +5”);
graficofunz(f);
g = funzione(“(x-5)/3 ”);
graficofunz(g);
h = funzione(“3*(x-5)/3+5”);
graficofunz(h);
stampa(“h è la funzione composta di f e g”);
………………………………….
………………………………….
…………………………………..
…………………………………..
…………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
Giudizio
10°
I
S
B
ND 
Date le rette r: y  3 x  1 e s: y   x  2 , descrivi “passo-passo” cosa esegue il seguente
programma. Alla fine formula come si potrebbe generalizzare questo tipo di problema.
Rifcart;
r = retta(3,1);
s = retta(-1,2);
x1 = (1-2)/(-1-3);
y1 = (-1*1-3*2)/(-1-3);
Stampa (“l’ascissa è =”, x1, “l’ordinata è =”, y1);
………………………………
………………………………
………………………………
………………………………………………………………………………………………
…………………………………..
………………………………………………………………………………………………
………………………………………………………………………………………………
………………………………………………………………………………………………
Giudizio
I
S
B
4
ND 
Quadro sinottico
Progetto "Matematica & Computer"
III Fase - Prima annualità del Triennio della Scuola Secondaria Sup.
a.s. 2001/2002 - 1° Test Modulo MatCos 1.6 - Gennaio 2002
classe
Istituto ___________________________________
di
_____________________________________
___
______________________
sezione ___
Docente
Quesiti
Alunno
1°
2°
3°
4°
5°
6°
7°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Legenda:
I = insufficente
S = sufficente
5
B = buono
ND = non data
8°
9°
10°
Progetto "Matematica & Computer"
III Fase - Prima annualità del Triennio della Scuola Secondaria Sup.
a.s. 2001/2002 - 1° Test Modulo MatCos 1.6 - Gennaio 2002
Istituto ______________________
di _____________________________________
classe
__
_____________________
Docente
sezione ___
Monitoroggio sui singoli quesiti e sul totale delle dieci domande
Insufficente
Sufficiente
Buono
1°
2°
3°
4°
5°
6°
7°
8°
9°
10°
Totale
6
Risposta non data
Totale
Tot.
Al. alunni
Per
dom.