II TEST MATCOS 1

Progetto
"Matematica & Computer "
III Fase - Prima annualità del triennio della scuola secondaria superiore
a.s. 2001/2002
Modulo MatCos 1.6
(Febbraio
Studente __________________________
2° Test
(Maggio 2002)
Cognome
Classe
1°
Nome
_________ Sezione _________
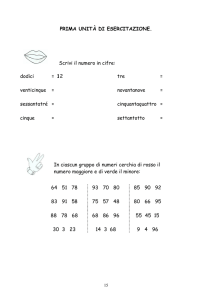
Scrivi un programma che disegni la circonferenza di centro C(1,-1) e raggio 3 e ne stampi i parametri
a,b,c della sua equazione cartesiana.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
I
Giudizio
2°
S
B
ND 
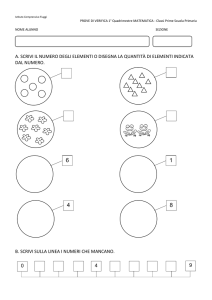
Dopo aver osservato attentamente il disegno riprodotto qui sotto, scrivi il programma che lo esegue.
………………………………………………………...
x
………………………………………………………...
r
………………………………………………………...
(0;4)
(0;2) 

………………………………………………………...
(2;2)
………………………………………………………...
………………………………………………………...

y
(2;0)
Giudizio
I
S
B
ND 
3°
Scrivi un programma che determina le componenti della forza che serve ad equilibrare la risultante
delle due forze F1 (7;2) e F2 (3;11) .
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
4°
I
S
B
ND 
Scrivi un programma che calcoli il valore della seguente espressione:
sen
13
15
20
  cos   sen 
3
4
3
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
5°
I
S
B
ND 
Scrivi un programma che disegna il grafico della seguente funzione: y  cos( x  2 )
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Cosa deduci?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
6°
I
S
B
ND 
Data la circonferenza di equazione x 2  y 2  2 e la retta r di equazione x  1, scrivi un programma
che determini la posizione della retta rispetto alla circonferenza.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
7°
I
S
B
ND 
Descrivi “passo-passo” cosa esegue il seguente programma, alla fine formula un enunciato relativo
ad esso.
………………………………………………………………………….
Rifcart;
A= punto(0,1);
B=punto(2,-1);
C= punto(-4,2);
c= circ(A,B,C,);
x0  c.centrox;
………………………………………………………………………….
………………………………………………………………………….
………………………………………………………………………….
………………………………………………………………………..
y 0  c.centroy;
r = c.raggio;
stampa(“l’ascissa del centro è = ”, x 0 , “l’ordinata del centro è = “, y 0 , “il raggio è =”, r);
Giudizio
8°
I
B
ND 
Descrivi “passo-passo” cosa esegue il seguente programma. Alla fine formula un enunciato
contenga le tue considerazioni.
Rifcart;
O= punto(0,0);
P= punto(3,4);
v =segmento_or(O,P);
A = punto;
B= punto;
colore(9);
r = retta(O,A);
s = retta(O,B);
colore(13);
r1 = parallela(s,P);
s1 = parallela(r,P);
H = intersezione(r,r1);
T = intersezione(s,s1);
Colore(5);
v1 =segmento_or(O,H);
v2 =segmento_or(O,T);
Giudizio
9°
S
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
………………………………………………………………………...
I
S
B
ND 
Descrivi “passo-passo” cosa esegue il seguente programma. Alla fine formula un enunciato che
contenga le tue considerazioni.
x = legginum(“valore dell’arco”);
a = sen(x);
b = cos(x);
k = (a^2+b^2);
stampa(“il valore di k è =”, k);
w = (a+b)^2;
stampa(“il valore di w è =”, w);
Se k<>w allora
che
Stampa (“ la somma dei quadrati è diversa dal quadrato della somma”);
altrimenti
stampa(“ho sbagliato qualcosa nella costruzione dello schema logico del programma”);
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
10°
I
S
B
ND 
Descrivi “passo –passo” cosa esegue il seguente programma.
Rifcart;
Colore(5);
f=funzione(“sin(x)”);
graficofunz(f);
colore (13);
g = funzione(“cos(x)”);
graficofunz(g);
………………………………………………………………………….
………………………………………………………………………….
………………………………………………………………………….
Implementa il programma al computer ed osserva attentamente i grafici delle due funzioni.
Quali analogie presentano? Quali differenze?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
I
S
B
ND 
Quadro sinottico
Progetto "Matematica & Computer"
III Fase - Prima annualità del Triennio della Scuola Secondaria Sup.
a.s. 2001/2002 - 2° Test Modulo MatCos 1.6 - Maggio 2002
classe
Istituto ___________________________________
di
_____________________________________
___
______________________
sezione ___
Docente
Quesiti
Alunno
1°
2°
3°
4°
5°
6°
7°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Legenda:
I = insufficente
S = sufficente
B = buono
ND = non data
8°
9°
10°
Progetto "Matematica & Computer"
III Fase - Prima annualità del Triennio della Scuola Secondaria Sup.
a.s. 2001/2002 - 2° Test Modulo MatCos 1.6 - Maggio 2002
Istituto ______________________
di _____________________________________
classe
__
_____________________
Docente
sezione ___
Monitoroggio sui singoli quesiti e sul totale delle dieci domande
Insufficente
1°
2°
3°
4°
5°
6°
7°
8°
9°
10°
Totale
Sufficiente
Buono
Risposta non data
Totale
Tot.
Al. alunni
Per
dom.
Progetto
"Matematica & Computer "
III Fase - Prima annualità del triennio della scuola secondaria superiore
a.s. 2001/2002
Modulo MatCos 1.6
(Febbraio
1°
Studente __________________________
2° Test
(Maggio 2002)
Per Licei Classici
Cognome
Classe
Nome
_________ Sezione _________
Scrivi un programma che rappresenti nel piano cartesiano il punto P(2, -3) e il grafico della funzione
y=2x-1
……………………………………………………………………………………………..
……………………………………………………………………………………………..
……………………………………………………………………………………………..
……………………………………………………………………………………………..
Giudizio
2°
I
S
B
ND 
Scrivi un programma che disegni nel piano cartesiano il triangolo di vertici A(1,0),
B(-1,-1), C(2,2).
……………………………………………………………………………………………….
……………………………………………………………………………………………….
……………………………………………………………………………………………….
……………………………………………………………………………………………….
Giudizio
3°
I
S
B
ND 
Scrivi un programma che disegni l’equazione della circonferenza di centro C(1,-1) e raggio 3.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
I
S
B
ND 
Date le seguenti rette di equazioni r : 5 x  15 y  8  0 e s: 6 x  2 y  1 , scrivi un programma che
verifichi l’incidenza tra le due rette.
4°
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
I
S
B
ND 
Data la seguente equazione di II grado x 2  2 x  3  0 , scrivi un programma che ne calcoli le
radici reali.
5°
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
6°
I
S
B
ND 
Siano A(0,3) e B(-1/3,0) due punti che individuano la retta r, scrivi un programma che disegni tale
retta.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Giudizio
7°
I
S
B
ND 
Dopo aver osservato attentamente il disegno riprodotto qui sotto, scrivi il programma che lo esegue.
y
……………………………………………………………
……………………………………………………………
……………………………………………………………
(0,3)
x
……………………………………………………………
……………………………………………………………
……………………………………………………………
Giudizio
I
S  ……………………………………………………………
B
ND 
8°
Descrivi “passo – passo” cosa esegue il seguente programma
a = legginum(“I coeff di x”);
b = legginum(“I coeff di y”);
c = legginum(“I termine noto”);
a1 = legginum(“II coeff di x”);
b1 = legginum(“IIcoeff di y”);
c 1= legginum(“II termine noto”);
d = a*b1-a1*b;
Se (d<>0) allora esegui;
xi = (c*b1-b*c1)/d;
yi= (a*c1-c*a1)/d;
stampa(“x = “, xi,” y= ”, yi);
fine;
altrimenti
stampa(“sistema senza soluzione”);
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
…………………………………………………………..
Giudizio
9°
I
S
B
ND 
Descrivi “passo-passo” cosa esegue il seguente programma.
Alla fine formula un enunciato che contenga le tue considerazioni.
Rifcart;
m=0;
n=1;
esegui finquando (n<= 7);
f = funzione(“m*x+n”);
grafico funz(f);
n = n+1;
colore(n);
fine;
…………………………………………………………………….
…………………………………………………………………….
…………………………………………………………………….
…………………………………………………………………….
…………………………………………………………………….
Giudizio
10°
I
S
B
ND 
Descrivi “passo-passo” cosa esegue il seguente programma.
Alla fine formula un enunciato che contenga le tue considerazioni.
Rifcart;
A= punto(0,1);
B=punto(2,-1);
C= punto(-4,2);
c= circ(A,B,C,);
x0  c.centrox;
…………………………………………………………………………….
…………………………………………………………………………….
…………………………………………………………………………….
y 0  c.centroy;
…………………………………………………………………………….
r = c.raggio;
stampa(“l’ascissa del centro è = ”, x 0 , “l’ordinata del centro è = “, y 0 , “il raggio è =”, r);
Giudizio
I
S
B
ND 
Quadro sinottico
Progetto "Matematica & Computer"
III Fase - Prima annualità del Triennio della Scuola Secondaria Sup.
a.s. 2001/2002 - 2° Test Modulo MatCos 1.6 - Maggio 2002
classe
Istituto ___________________________________
di
_____________________________________
___
______________________
sezione ___
Docente
Quesiti
Alunno
1°
2°
3°
4°
5°
6°
7°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Legenda:
I = insufficente
S = sufficente
B = buono
ND = non data
8°
9°
10°
Progetto "Matematica & Computer"
III Fase - Prima annualità del Triennio della Scuola Secondaria Sup.
a.s. 2001/2002 - 2° Test Modulo MatCos 1.6 - Maggio 2002
Istituto ______________________
di _____________________________________
classe
__
_____________________
Docente
sezione ___
Monitoroggio sui singoli quesiti e sul totale delle dieci domande
Insufficente
1°
2°
3°
4°
5°
6°
7°
8°
9°
10°
Totale
Sufficiente
Buono
Risposta non data
Totale
Tot.
Al. alunni
Per
dom.