Risoluzione Numerica delle Equazioni

appunti java – Capitolo 13
pag.
1
13. Risoluzione Numerica delle Equazioni.
Data l'equazione nella forma f(x) = 0 , a seconda della natura della f le equazioni si classificano in:
 Algebriche
 Trascendenti
Le equazioni algebriche a loro volta si distinguono in:
 Razionali
 Irrazionali
Quando si risolve una equazione si deve specificare l'insieme nel quale si ricercano le soluzioni o
radici; se l'insieme non viene indicato, di solito si sottintende R .
In R siamo in grado di risolvere equazioni di:
 1° grado
 2° grado
 riconducibili a 1° grado e 2° grado.
Si dimostra che una equazione algebrica razionale intera di grado n ha n soluzioni, non
necessariamente tutte reali.
Per risolvere le equazioni di 1° grado sono sufficienti i principi delle equazioni, per quelle di 2°
esiste la formula risolutiva.
Esistono formule risolutive per le equazioni algebriche di grado n superiore a 2?
Per n = 3 si hanno le formule di Cardano (1545); il metodo risolutivo è dovuto a Scipione Dal
Ferro(1515).
Per n = 4 si ha la formula di Ludovico Ferrari (1540 circa).
Per n  5 Paolo Ruffini (1765  1822) stabilì che non esistono formule generali; la dimostrazione di
Ruffini era incompleta, ma Niels Abel fornì una dimostrazione rigorosa nel 1826.
Se non esistono formule risolutive generali per le equazioni algebriche … non esistono certo
formule risolutive per le equazioni trascendenti.
Quando non è possibile conoscere il valore esatto delle soluzioni ci si accontenta di conoscere un
valore approssimato delle soluzioni stesse ottenuto applicando uno dei metodi numerici per la
risoluzione numerica delle equazioni.
Prima di applicare un algoritmo per ottenere un valore approssimato delle soluzioni reali di una
equazione del tipo f(x) = 0 , occorre stabilire
1. se le soluzioni esistono
2. quante sono le soluzioni.
Le soluzioni dell'equazione f(x) = 0 si possono interpretare graficamente come le ascisse dei punti
di intersezione con l'asse delle x della funzione a variabili reali di equazione y = f(x) .
appunti java – Capitolo 13
pag.
2
Uno studio qualitativo di y = f(x) permette di
1. conoscere il numero delle soluzioni
2. localizzare le soluzioni.
13.1 La separazione delle soluzioni
In particolare si parla di limitazione delle soluzioni quando si è determinato l'intervallo [a, b] cui
appartengono tutte le soluzioni dell'equazione, non esistono, cioè, soluzioni non appartenenti
all'intervallo [a, b].
Si parla, invece, di separazione delle soluzioni quando si individua un insieme di sottointervalli di
[a, b] disgiunti, non necessariamente chiusi, all'interno dei quali cade una e una sola soluzione.
y
a
y = f(x)
d
c
x1
x2
b
x3
x
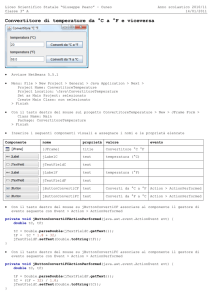
Con riferimento alla figura l'intervallo [a, b] rappresenta una limitazione delle soluzioni, mentre i
sottointervalli [a, c] , [c, d] e [d, b] rappresentano una separazione delle soluzioni.
13.2 Teorema dell'Esistenza degli zeri
Per la limitazione delle radici si può utilizzare il Teorema dell'Esistenza degli zeri
Teorema dell'Esistenza degli zeri
Sia f una funzione continua in [a, b], se essa assume negli estremi dell'intervallo valori di segno
discorde, cioè f(a) f(b) < 0 , allora esiste almeno un punto, c, interno all'intervallo [a, b] in cui
annulla, cioè f(c) = 0.
Se, inoltre, f è anche monotona in [a, b] essa si annulla in un unico punto interno all'intervallo [a,b].
Se per c]a, b[ si ha f(c) = 0 allora c è chiamato zero della funzione f.
Esempio
Data l'equazione trascendente 3sin x – x = 0 limitare e separare le radici.
appunti java – Capitolo 13
pag.
3
Si osserva che x = 0 è soluzione dell'equazione, ma è l'unica soluzione o ne esistono altre?
Nella figura seguente si riporta il grafico di y = 3sin x – x.
Dal grafico si osserva che la curva interseca l'asse x in tre punti: uno di ascissa 0 e gli altri due di
ascissa  e .
Le tre radici cadono nell'intervallo [5, +5] infatti f(5) = 7.876772… > 0 e f(5) = –7.876772…< 0
[5, 5] è una limitazione delle radici.
Anche [4, 4] è una limitazione delle radici infatti f(4) = 6.270407… > 0 e f(4) = –6.270407…< 0
e così [, ] infatti f() =  > 0 e f() =  < 0.
   



Considerando l'ultima limitazione [, ] i sottointervalli   ,   ,  ,  e  ,  
2  2 2

2

costituiscono una separazione delle radici.
Non è molto immediata la costruzione del grafico di y = 3sin x – x e di solito si procede nel modo
seguente.
Scritta l'equazione nella forma 3sin x= x essa può essere interpretata come l'equazione risolvente il
sistema
 y  3sinx

y  x
Le soluzioni dell'equazione data saranno le ascisse degli eventuali punti di intersezione delle due
curve di equazione y = 3sin x e y = x , i grafici delle quali sono sicuramente più semplici da
tracciare.
Le due curve si intersecano in tre punti: uno di ascissa 0 e gli altri due di ascissa  e 
con 0 <  <  .
appunti java – Capitolo 13
pag.
y
4
y=x
y = 3sinx
x
Infatti per x = 0 si ha sin 0 = 0 , per x =  si ha sin  = 0 e per x =  si ha sin () = 0 , la
funzione y = x è sempre crescente nel suo dominio e y = 3sin x ha per codominio  3, 3 .
   
 
 



Inoltre 3sin     3 e 3sin    3 pertanto gli intervalli   ,   ,  ,  e  ,  
2  2 2
2
 2

2

costituiscono una separazione delle radici.
13.3 Metodi Numerici per la risoluzione delle equazioni
13.3.1 Metodo di Bisezione o Dicotomico
Sia data l’equazione f(x) = 0 e sia s l’unica soluzione appartenente all’intervallo [a, b], cioè f(s) =
0 con s[a, b] ; s si può interpretare come l’ascissa del punto di intersezione del grafico della
funzione di equazione y = f(x) con l’asse delle x .
Condizioni per applicare il metodo
y = f(x)
s[a, b]
f(a) e f(b)
continua in [a, b]
unica
discordi
y
y=f(x)
(b, f(b))
(x3, f(x3))
a
x1
x2
x3
(a, f(a))
(x2, f(x2))
(x1, f(x1))
b
x
appunti java – Capitolo 13
Si calcola x1 
pag.
ab
2
se
f(x1) = 0
f(x1)  0
x1 è soluzione dell'equazione soluzione
si determina l’intervallo cui appartiene s
f(a) f(x1)<0
f(x1) f(b) <0
s[a, x1]
s[x1,b]
se
Si ripete il procedimento e si ottiene così una successione di intervalli cui appartiene s.
Se si indica con ai l’estremo sinistro e con bi l’estremo destro si ha:
[an, bn]  [an-1 , bn-1]  ... [a1 ,b1]  [a, b]
Quando si arresta il procedimento?
 a  bn 
Se f  n
  0,
 2 
s
a n  bn
.
2
 a  bn 
Se f  n
  0?
 2 
Fissata una precisione  il procedimento si può arrestare quando |an - bn |<  .
È possibile stimare a priori il valore di n.
Poiché bn  a n 
2n 1 
ba

n  1  log 2
ba
, si ha
2n
ba

2n
e
ba
  da cui si ottiene
2 n 1
 2n
ba

n
Quindi la relazione
n  1  log 2
ba
  è verificata per
2n
ba

Un altra condizione di arresto potrebbe essere:
 b  an 
f n
 
 2 
È un buon criterio di arresto ? Non sempre. Dipende dall’andamento della funzione f.
5
appunti java – Capitolo 13
pag.
6
Sono poche le condizioni su y = f(x) per l’applicabilità del metodo: solo la continuità.
Vantaggi e Svantaggi del metodo
Vantaggi
Semplicità
Svantaggi
Convergenza lenta; con altri metodi la precisione richiesta si raggiunge in un numero
inferiore di iterazione del metodo.
13.3.2 Metodo della Corda
Sia data l’equazione f(x) = 0 e sia s l’unica soluzione appartenente all’intervallo [a, b], cioè f(s) =
0 con s[a, b] ; s si può interpretare come l’ascissa del punto di intersezione del grafico della
funzione di equazione y = f(x) con l’asse delle x .
Condizioni per applicare il metodo
y = f(x)
s[a, b]
f(a) e f(b)
continua in [a, b]
unica
discordi
y=f(x)
y
(x1,f(x1))
(b,f(b))
a
x2
x3
x1
b
x
(x2,f(x2))
(a,f(a))
Si calcola l'equazione della retta passante per i punti (a, f(a)) e (b, f(b))
xa
y  f (a)

b  a f (b)  f (a)
che intersecherà l’asse x in un punto di ascissa x1, interno all’intervallo [a, b]
e si determina quindi il valore di x1 ponendo y=0
x1  a
f (a)

ba
f (b)  f (a)
ba
x1  a 
f (a)
f (b)  f (a)
Se
f(x1) = 0
f(x1)  0
x1 è soluzione dell'equazione
si determina l’intervallo cui appartiene s
f(a) f(x1)<0
f(x1) f(b) <0
s[a, x1]
s[x1,b]
Se
appunti java – Capitolo 13
pag.
7
si ripete il procedimento e si ottiene così una successione di valori xn ognuno dei quali approssima s.
xn n
 s

Quando si arresta il procedimento?
Fissata una precisione , il procedimento si può arrestare quando, presi due valori consecutivi della
sequenza, xn e xn-1 , risulta |xn - xn-1 |< 
Si consideri ora il seguente caso
y
y=f(x)
(b,f(b))
a
x1
x2
x3
b
x
(x3,f(x3))
(a,f(a)
)
(x2,f(x2))
(x1,f(x1))
Se si applica il procedimento si osserva che un estremo dell'intervallo in cui cade s non è mai
modificato, con riferimento alla figura precedente l'estremo b .
Se si calcola l'equazione della retta passante per i punti (x1, f(x1)) e (b, f(b)) si ha
x  x1
y  f ( x1 )

b  x1 f (b)  f ( x1 )
e l'ascissa, x2, del suo punto d'intersezione con l'asse delle x vale
x2  x1 
b  x1
f ( x1 )
f (b)  f ( x1 )
Se si ripete ancora il procedimento si avrà
x3  x 2 
b  x2
f ( x2 )
f (b)  f ( x2 )
…
Procedendo si ha la formula ricorrente xn  xn1 
b  xn1
f ( xn1 )
f (b)  f ( xn1 )
Qualora non si modifichi l'estremo sinistro a si avrà
a  xn 1
xn  xn 1 
f ( xn 1 )
f (a)  f ( xn1 )
Per avere una formula ricorrente, un estremo dell’intervallo iniziale cui appartiene s deve rimanere
fisso e questo si verifica se la funzione y = f(x) nell’intervallo [a,b] non modifica mai la sua
concavità.
appunti java – Capitolo 13
8
pag.
La funzione y = f(x) dovrà pertanto essere anche derivabile due volte in [a,b] con f ’’(x) di segno
costante in [a,b].
13.3.3 Metodo di Newton o della Tangente
Sia data l’equazione f(x) = 0 e sia s l’unica soluzione appartenente all’intervallo [a, b], cioè f(s) =
0 con s[a, b] ; s si può interpretare come l’ascissa del punto di intersezione del grafico della
funzione di equazione y = f(x) con l'asse delle ascisse.
Si consideri la situazione rappresentata nella figura seguente:
y=f(x)
y
(b,f(b))
a
x1 x2 x3
b
(x2,f(x2))
x
(x1,f(x1))
(a,f(a))
Dal punto (a, f(a)) si è tracciata la retta tangente alla curva di equazione y = f(x) e con x1 si è
indicata l’ascissa del punto di intersezione della tangente con l'asse x : x1 è una prima
approssimazione di s .
Poiché f(x1)  0 , dal punto(x1, f(x1)) si è tracciata la retta tangente alla curva e si è indicata con x2
l’ascissa del punto di intersezione della tangente con l'asse x : x2 è ancora una approssimazione di s .
Reiterando il procedimento si ottiene una successione di valori xn ognuno dei quali approssima s e,
 s .
al tendere di n all'infinito, xn converge ad s: xn n

Si osserva che per applicare il metodo, non solo si deve avere y = f(x) continua in [a, b], s[a, b]
unica e f(a) e f(b) discordi, ma deve esistere la tangente alla curva in ogni suo punto e pertanto la
funzione deve essere derivabile in ogni punto dell'intervallo ]a, b[ (anche in un intorno di a e di b).
Non si devono, inoltre, verificare situazioni come quelle rappresentate nei diagrammi seguenti
y
y
y=f(x)
(b,f(b))
(b,f(b))
a
a
b
(a,f(a)
)
x
b
(a,f(a))
x
appunti java – Capitolo 13
pag.
9
Affinché non si verifichino situazioni come quelle rappresentate, la funzione deve essere:
a) derivabile due volte in ogni punto dell'intervallo ]a, b[ (anche in un intorno di a e di b)
b) avere derivata prima e derivata seconda diverse da zero e con segno costante in ]a, b[ .
Si calcola l'equazione della retta tangente alla curva nel punto (a, f(a))
y  f (a)  f ' (a)( x  a)
e quindi l'ascissa, x1, del suo punto d'intersezione con l'asse delle x .
x1  a 
f (a)
f ' (a)
Si può ripetere il procedimento e calcolare l'equazione della tangente alla curva nel punto (x1, f(x1))
y  f ( x1 )  f ' ( x1 )( x  x1 ) e quindi l'ascissa, x2, del suo punto d'intersezione con l'asse delle x .
x2  x1 
Si ha
f ( x1 )
f ' ( x1 )
f ( xn 1 )
nella quale ogni
f ' ( xn 1 )
valore è espresso in funzione del valore precedente, partendo da un valore iniziale x0 che può
coincidere con a o con b . Ogni valore della successione xn approssima s .
Si dimostra che la successione ottenuta converge a s
xn n
 s .

Non si può procedere all'infinito. Quando si arresta il procedimento?
Fissata una precisione , il procedimento si può arrestare quando, presi due valori consecutivi della
sequenza, xn e xn-1 , risulta|xn - xn-1 |< 
Da quale estremo partire (a, f(a)) o (b, f(b)) ?
Reiterando il procedimento si ha la formula ricorrente
xn  xn 1 
Si considerino i seguenti grafici:
y
y
x
y
x
y
x
x
appunti java – Capitolo 13
pag.
10
Dall'osservazione dei grafici riportati si può concludere che il procedimento può iniziare
dall'estremo nel quale la funzione ha lo stesso segno della derivata seconda.
Dal punto di vista pratico, se si verificano le condizioni per applicare il metodo (derivata prima e
seconda diverse da zero e con segno costante), il procedimento numerico può avere inizio da uno
qualsiasi dei due estremi dell’intervallo purché, se il primo valore calcolato, x1, non appartiene
all’intervallo, si ripeta il procedimento partendo dall’altro estremo.
13.4. Progetto di algoritmi per la determinazione degli zeri
13.4.1. Algoritmo di Bisezione semplificato
Con la parola “semplificato” si intende un algoritmo che termina solo se sono verificate
strettamente le condizioni di convergenza.
CONDIZIONI di Convergenza:
 E’ certo che f(x) è definita e continua in [a, b]
 E’ certo che f(a)*f(b)<0 ( Se ho delimitato una sola soluzione ancora meglio)
 E’certo che ε (tol), che è il massimo errore assoluto con cui si desidera determinare la
soluzione NON è inferiore all’ultima cifra significativa con cui un double è rappresentabile
nel linguaggio (circa 13 cifre circa in Java, avvero tol>10-13 )
La successione che converge alla soluzione è la seguente
x1=(a+b)/2
x2= (a+x1)/2
se f(a)*f(x1)<0 oppure x2= (b+x1)/2 se f(b)*f(x1)<0
…..
xn=(xn-1+xn-2)/2
se f(xn-1)*f(xn-2) <0
La condizione di terminazione dell’iterazione ciclica è | xn-xn-1| < tol
13.4.2. Il progetto di una classe java per contenere gli algoritmi.
Si tratta di un gruppo di algoritmi numerici che possono essere utilizzati da un programma main che
li invoca e saranno progettati come metodi Java statici.
La classe Zeri sarà il nome del contenitore. Il seguente disegno mostra i soli metodi necessari. Il
metodo bisez implementa quello che abbiamo chiamato algoritmo di bisezione “semplificato”.
Zeri
- static double f(double x)
+static double bisez(double a, b, tol)
Si noti che la classe non ha costruttori e non ha attributi in quanto semplice contenitore di metodi
statici.
Il metodo privato - static double f(double x) deve contenere l’espressione analitica della funzione di
cui si desidera determinare lo zero approssimato.
Il metodo pubblico +static double bisez(double a, b, tol) implementa l’algoritmo con l’evidente
significato dei parametri che riceve.
appunti java – Capitolo 13
pag.
11
La codifica che segue è quella più banale date le condizione restrittive imposte per la terminazione.
Si è supposto di voler determinare lo zero della funzione y=sen x delimitata dall’intervallo
[a=1, b=4] si ricorda che sen x ha una zero a pigreco che vale circa 3,14
public class Zeri {
public static double f(double x) {
return Math.sin(x);
}
public static double bisez(double a, double b, double tol) {
boolean trovato=false;
double yc=0,xc=0,delta=Math.abs(b-a);
double ya=f(a), yb=f(b);
while ((delta>=tol && !trovato)) {
xc=(a+b)/2;
yc=f(xc);
if (yc*ya<0) { b=xc; yb=yc; /* nuovi estremi a, c */ }
else
if (yc*yb<0) { a=xc; ya=yc; /* nuovi estremi c, b */
else if (yc==0) trovato=true;
delta=Math.abs(b-a);
}
return xc;
}
}
di seguito il main() di prova:
public class banale{
public static void main(String arg[]) {
double tol=0.0001, a=1,b=4;
double r=Zeri.bisez(a,b,tol);
System.out.println("la radice vale "+r+"+-"+tol);
}
}
13.4.3. Algoritmo di Bisezione meno banale
Con la parola “meno banale” si intende un algoritmo che termina anche se NON sono verificate
TUTTE le condizioni di convergenza e anche se la f(x) NON ha zeri nell’intervallo.
CONDIZIONI di TERMINAZIONE:
 Se f(x) non è definita in [a, b] termina con la restituzione di una segnalazione adeguata.
 Se f(a)*f(b)>0 termina con la restituzione di una segnalazione adeguata.
 Se ε (tol) o inferiore all’ultima cifra significativa con cui un double è rappresentabile nel
linguaggio (circa 13 cifre circa in Java, avvero tol>10-13 ), termina con la restituzione di una
segnalazione adeguata.
 Se trova lo zero termina con la restituzione del valore di xn, di f(xn) e del numero di
iterazioni impiegate per determinare la soluzione.
La successione che converge è identica a quella sopra indicata
appunti java – Capitolo 13
pag.
12
Per far restituire le diverse situazioni di terminazione è necessario progettare una classe Sol che
conterrà un Oggetto Sol stampabile che non consisterà semplicemente un double.
Ampliamento della classe Zeri e progetto della classe Sol
Zeri
- static double f(double x)
+static double bisez(double a, b, tol)
+ static Sol bisez(double a, b, tol, int Maxiter)
Sol
-
double X, Y, TOL;
int IT, MAXITER, E ;
+ Sol(double x, y, tol, int Iter, Maxiter, err)
+ double getX()
+ double getY()
+ String toString()
Gli attributi di Sol corrispondono a tutte le informazioni che può restituire la soluzione
dell’algoritmo:
 se E=0 l’algoritmo è terminato correttamente e i dati x,y,to,it hanno un significato evidente.
Il metodo toString() restituisce la stringa con tutte le informazioni.
 Se E=1 Si è verificato che f(a)*f(b)>0 e il metodo toString() restituisce l’informazione.
 Se E=2 La f(x) non è definta in [a,b].
 Se E=3 l’algoritmo non converge dopo MAXITER iterazioni. (con bisezione l’unica
possibilità e che abbiate assegnato tol=0.


Il costruttore Sol(…) viene invocato da bisez() con gli opportuni parametri di terminazione
String toString() ; restituisce la Stringa stampabile di una Sol
 double getX() ; double getY();
sono stati progettati per restituisce il solo xo o il yo.
La codifica che segue mostra quanto illustrato (si lascia la codifica di Sol come esercizio):
public static Sol bisez(double a, double b, double tol, int maxiter) {
int iter=0; int err=0; boolean trovato=false; double ya,yb,yc=0,xc=0,xb=b,xa=a,delta=(b-a);
if ( f(a)==0) {xc=a; yc=f(a); trovato=true;}
else if ( f(b)==0) {xc=b; yc=f(b); trovato=true;}
else if (f(a)*f(b)>0) err=1;
else if((""+f(a)).equals("NaN") || (""+f(b)).equals("NaN")) err=2;
else { // f(a) and f(b) <0
ya=f(xa); yb=f(xb);
while ((delta>=tol) && (iter<=maxiter)&& (err==0) && (!trovato)) {
xc=(a+b)/2; yc=f(xc);
if ((""+yc).equals("NaN")) err=2;
else { // funzione definita
iter++; delta=Math.abs(xc-a);
if (yc*ya<0) { b=xc; yb=yc; /* nuovi estremi a, c */ }
else if (yc*yb<0) { a=xc; ya=yc; /* nuovi estremi c, b */ }
else if (Math.abs(yc)==0) trovato=true;
else if (ya*yc>0) err=1;
} // end else funzione definta
} // end while
} // end else f(a) and f(b) <0
if (delta<tol) trovato=true;
else if (iter>maxiter) { xc=Double.NaN; yc=Double.NaN; err=3; }
else if (err!=0) { xc=Double.NaN; yc=Double.NaN; }
return new Sol(xc,yc,tol,iter,maxiter,err);
} // end bisez
appunti java – Capitolo 13
pag.
13
13.4.4. Progetto dell’algoritmo di Newton semplificato.
Con la parola “semplificato” si intende un algoritmo che termina solo se sono verificate
strettamente le condizioni di convergenza.
Condizioni di Convergenza:
 E’ certo che f(x) e f’(x) sono definite e continue in [a, b]
 E’ certo che La soluzione esiste in [a,b];
 I metodo converge sicuramente, esempio f(x) e continua e f’’(x) mantiene sempre lo stesso
segno, con x in [a,b])
Controlli da testare :
 Ho trovato la soluzione esatta [y=f(x)=0] quindi interrompo e restituisco la soluzione
 Ho trovato la soluzione approssimata (xn-xn-1)<tol
 La retta tangente ha coefficiente angolare [f’(x)=0] è impossibile continuare. Interrompo con
messaggio.
La successione che converge alla soluzione è la seguente
x0=a
x1=x0-f(x0)/f’(x0)
…..
xn=xn-1- f(xn-1)/f’(xn-1)
La condizione di terminazione dell’algoritmo è | xn-xn-1| < tol
La classe Zeri sarà così ampliata:
Si noti che:
 Il metodo df(..) contiene
l’espressione analitica della
derivata prima di f(x).
 Il metodo newton(..) esige un
solo punto a per avviare il
ciclo iterativo.
Il codice di newton semplificato è:
Zeri
- static double f(double x)
- static double df(double x)
+ static double bisez(double a, b, tol)
+ static Sol bisez(double a, b, tol, int Maxiter)
+ static double newton(double a, tol)
public static double newton (double a, double tol) {
double xn_1=a; boolean err=false, trovato=false;
double y=f(xn_1), dy=df(xn_1);
double xn=xn_1-y/dy ;
if (y==0) trovato=true;
if (dy==0) err=true;
double delta=Math.abs(xn-xn_1) ;
while (delta>tol && !err && !trovato) {
xn_1=xn; y=f(xn_1) ; dy=df(xn_1) ;
xn= xn_1-y/dy ;
if (y==0) trovato=true;
if (dy==0) err=true;
delta=Math.abs(xn-xn_1) ;
}
if (err==true ) {
System.out.println("Tangente orizzontale");
System.exit(1); }
return xn ;
}
appunti java – Capitolo 13
pag.
14
13.4.5. Progetto dell’algoritmo di Newton non banale.
Per progettare l’Algoritmo di Newton in modo che termini quasi sempre, in analogia al caso
Bisezione non banale, si devono prendere in esame le seguenti situazioni:
1) nell’intestazione si deve passare la variabile Maxiter che controlla l’entrata in cicli infiniti
2) restituire un Oggetto Sol (come in Bisezione NON Banale)
3) controllare sia l’esistenza di f(x) che quella di f’(x)
4) verificare che la retta tangente non abbia coefficiente angolare [f’(xn)=0]
5) controllare se xn, f(xn)=0 è uno zero esatto
L’adeguamento della classe Sol, il nuovo metodo newton(…) con la relativa intestazione e il main
di prova sono assegnati come esercizio da svolgere facendo riferimento al codice di Bisezione.
13.4.6 Progetto dell’algoritmo del rapporto incrementale (quasi Newton).
Se non si dispone della f’(x) è possibile utilizzare un metodo “analogo” al metodo di Newton sostituendo alla derivata
di f(x) in un punto il suo rapporto incrementale in tale punto scegliendo con attenzione il valore dell’incremento h.
La successione del metodo del rapporto incrementale diviene:
x0=a
x1=x0-f(x0)/[f(x0+h)- f(x0)]/h
…..
xn=xn-1- f(xn-1)/ [f(xn-1+h)- f(xn-1)]/h
Come deve essere il valore di h ? molto piccolo ma non inferiore alla precisione (numero di cifre significative) dei
numeri double del sistema. Esempio h=1e-10 è corretto con i double di Java, mentre h=1e-20 NO. I double di Java
hanno 15 cifre significative quindi 10-15 è il limite di sicurezza.
Progettare l’algoritmo sia Semplificato che Non Banale con questo metodo.
1.
Metodo semplificato: gli unici controlli da testare sono:
o Ho trovato una soluzione esatta [y=f(x)=0] quindi interrompo e restituisco la soluzione
o La retta “Quasi” tangente ha coefficiente angolare [m=f(x+h)-f(x)/h=0] è impossibile continuare.
Interrompo con messaggio. [Non è necessaria la f’(x) ]
2.
Metodo Non Banale:
o Desumere da bisezione Newton i controlli che è opportuno testare
L’adeguamento della classe Sol, il nuovo metodo newton(…) con la relativa intestazione e il
main di prova sono assegnati come esercizio da svolgere facendo riferimento al codice di
Bisezione.
appunti java – Capitolo 13
pag.
15
13.E – Esercizi
Esercizi sugli zeri
1. progettare un programma che "implementi l’algoritmo della corda”.
Indicazioni: fare l’ipotesi semplificata della convergenza.
Richieste: Ampliare la classe Zeri progettata in precedenza.
2. progettare un programma che "implementi l’algoritmo della corda non banale”.
Indicazioni: fare ipotesi sulle condizioni di terminazione in analogia al precedente algoritmo di
Bisezione.
Richieste: Ampliare la classe Zeri progettata in precedenza e verificare l’adeguatezza della classe Sol.
3. progettare un programma che "implementi l’algoritmo del rapporto incrementale”.
Indicazioni: fare l’ipotesi semplificata della convergenza.
Richieste: Ampliare la classe Zeri progettata in precedenza.
4. progettare un programma che "implementi l’algoritmo del rapporto incrementale non
banale”.
Indicazioni: fare ipotesi sulle condizioni di terminazione in analogia al precedente algoritmo di
Newton non banale.
Richieste: Ampliare la classe Zeri progettata in precedenza e verificare l’adeguatezza della classe Sol.