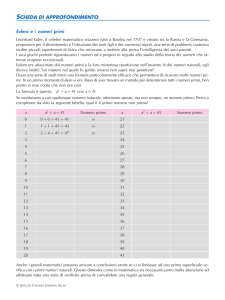
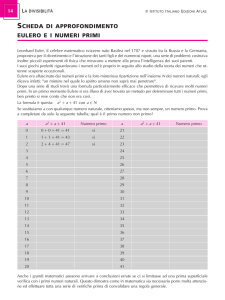
Teoria dei numeri
Lezione del giorno 4 aprile 2008
Esponenziazione modulare
Sia m>1 un intero, fissiamo un esponente intero positivo hm, un elemento [x] in Zm (con 0x<m),
e poniamoci il problema di trovare un algoritmo per calcolare la potenza [x h] (equivalentemente la
riduzione xhmodm).
Esporremo un algoritmo molto efficiente (di complessità polinomiale), detto esponenziazione
modulare.
Siano k=L(m), t=L(h) le lunghezze (binarie) del modulo m e dell’esponente h: essendo hm si ha
tk. Poiché t rappresenta il numero di cifre binarie di h, si ha:
h=at-12t-1+ at-22t-2+….+a12+a0
(con ai=0,1)
Costruiamo una successione y0,y1,...,yt di numeri interi ponendo:
2 a
y0=1; per ogni i>0 yi= (y i1 x t i ) modm
Ogni elemento della successione yi è una riduzione modulo m, dunque 0≤yi<m; inoltre ogni
elemento della successione yi (con i>0) si può calcolare (a partire dal precedente) con la riduzione
di due prodotti con fattori <m (il quadrato di yi-1 e il prodotto del risultato per x a t i , quest’ultimo
uguale ad x oppure ad 1, poiché l’esponente at-1 è =0,1), dunque (come visto esaminando la
complessità del prodotto in Zm) il calcolo di ogni yi con i>0 ha complessità O(k2); il numero degli
elementi della successione da costruire è tk, dunque complessivamente l’algoritmo ha complessità
polinomiale O(k3).
Dimostriamo che tale algoritmo fornisce il valore della riduzione x kmodm: precisamente
dimostriamo che si avrà yt= xkmodn.
Dimostriamo prima per induzione che per ogni i con 1it, si ha:
i -2
i -1
yi x (a t -1 2 a t -2 2 . a t -i1 2 a t -i ) (mod m)
2 a t -1
(*)
a t -1
Si ha y1= (y 0 x ) modm quindi y1 x (mod m), e la (*) è vera per i=1.
Supponiamo (*) vera per i e dimostriamola per i+1: si hanno le seguenti congruenze modulo m
i -1
i -1
i
i
yi+1 (y i 2 x a t i-1 ) x[2(at -1 2 a t -2 2 . a t -i1 2 a t -i ) a t -i-1 ] = x (a t -1 2 a t -2 2 . a t -i 2 a t -i-1 )
quindi la (*) è vera per i+1.
In particolare, per i=t, si ottiene la congruenza:
yt x (a t-1 2 a t-2 2 . a1 2 a 0 ) = xk (mod n)
Poiché, come già notato, si ha 0≤yi<m, la precedente congruenza implica che yt = xkmodm.
Notiamo che nell’algoritmo anche la grandezza dei numeri coinvolti nei calcoli è limitata: ad ogni
passo si moltiplicano fattori <m e si riduce il risultato modulo m, quindi si lavora sempre con
numeri <m2.
t -1
t -2
Esempio.
Siano m=341, x=2, e calcoliamo [2340] in Z341.
Si tratta quindi di calcolare con l’esponenziazione modulare la riduzione 2340mod341.
La rappresentazione binaria dell’esponente 340 è:
340 = 128+027+126+025+124+023+122+021+0 = (101010100)2
Seguendo i passi dell’algoritmo, costruiamo la successione y0,y1,y2,y3,y4,y5,y6,y7,y8,y9 con y0=1 e
per i>0 yi= (yi 12 2a 9i ) mod341 , dove at-i è la cifra binaria coefficiente di 2t-i in 340.
Si ha:
y1= (12 2a 8 ) mod341=2 ; y2= (12 2a 7 ) mod341=4 ; y3= (4 2 2a 6 ) mod341=32 ; y4= (32 2 2a 5 ) mod341=1 ;
y5= (12 2a 4 ) mod341=2 ; y6= (2 2 2a 3 ) mod341=4 ; y7= (4 2 2a 2 ) mod341=32 ; y8= (3222a1 ) mod341=1 ;
y9= (12 2a 0 ) mod341=1=2340mod341.
Possiamo allora concludere che [2340]=[1] in Z341.
Funzione di Eulero
Abbiamo già definito funzione di Eulero dell’intero m>1 la cardinalità (m) del gruppo Zm* degli
elementi invertibili del monoide Zm (rispetto al prodotto), o equivalentemente il numero degli interi
a coprimi con m tali che 1am (in questo senso la funzione è definita anche per m=1: (1)=1).
Esempio.
Se m=pk con p primo e k>0, un numero naturale a non è coprimo con m se e solo se a è multiplo di
p: infatti se mcd(a,m)=d>1, essendo dpk si ha d=ph con 0<hk (per la fattorizzazione unica) da cui
pd e per transitività pa; viceversa se pa allora, posto d=mcd(a,pk), si ha ppk dunque pa.
Dunque, per calcolare (pk), dobbiamo sottrarre al numero pk di tutti i naturali compresi fra 1 e pk il
numero di tutti quelli che sono multipli di p: poiché i multipli di p (compresi fra 1 e pk) sono in
numero di m/p=pk-1, si ottiene la formula per il calcolo della funzione di Eulero per potenze di
primi:
(pk)=pk-pk-1=pk-1(p-1)
In particolare se m=p primo, si ha:
(p)=p-1
Teorema.
Se m,n>1 sono naturali coprimi si ha (mn) = (m)(n).
Dimostrazione:
Definiamo la funzione f: Zmn Zm x Zn ponendo f([x]mn) = ([x]m , [x]n) .
La f è surgettiva: infatti per ogni coppia ([a]m , [b]n) il Teorema Cinese del Resto assicura
l’esistenza di qualche soluzione intera del sistema:
x a (mod m)
x b (mod n)
e si ha f([x]mn) = ([x]m , [x]n)= ([a]m , [b]n).
Avendo dominio e codominio stessa cardinalità mn, la f è biunivoca.
E’ facile verificare che [x]mn è invertibile in Zmn se e solo se [x]m é invertibile in Zm e [x]n é
invertibile in Zn .
Dunque la restrizione di f al gruppo Zmn* fornisce una funzione biunivoca fra Zmn* e Zm* x Zn* ,
per cui si conclude che (mn)= Zmn* = Zm* x Zn*= Zm* Zn*=(m)(n) .
Il Teorema precedente si può estendere facilmente per induzione al caso di più di 2 numeri naturali:
se m1,m2,….,mn sono naturali >1 a 2 a 2 coprimi, si ha (m1m2…mn)= (m1) (m2)… (mn).
Basta infatti procedere per induzione con base n=2 utilizzando (come nella dimostrazione del
Teorema Cinese del Resto) l’osservazione che se m1,m2,….,mn, mn+1 sono a 2 a 2 coprimi anche
(m1m2….mn), mn+1 sono coprimi.
Sia n>1 un numero naturale. Possiamo fattorizzare in modo unico n nel prodotto di numeri primi, e
se raccogliamo sotto forma di potenza i fattori primi uguali, possiamo fattorizzare n in prodotto di
potenze di primi distinti:
n = p1k1 p 2 k 2 ....p r k r
pi primi distinti, ki interi >0 .
Conoscendo la fattorizzazione di n, si può facilmente calcolare la funzione di Eulero (n).
Infatti si può notare che due potenze di primi distinti ph, qk sempre sono numeri coprimi: se per
assurdo fosse d=mcd(ph,qk)>1, considerato un divisore primo p0 di d si avrebbe p0ph, p0qk,
dunque p0p, p0q e infine p0=p=q, contraddizione.
Basta allora applicare il Teorema precedente e la formula per il calcolo della funzione di Eulero per
potenze di primi per ricavare:
(n) = (p1k1 ) (p 2 k 2 ).... (p r k r ) = p1k1 1 (p1 - 1)p 2 k 2 1 (p 2 - 1)....p r k r 1 (p r - 1)
Si può notare che il risultato precedente si può anche riformulare nel modo seguente:
La formula precedente fornisce anche un algoritmo per calcolare la funzione di Eulero di n,
conoscendo la sua fattorizzazione in prodotto di primi.
Attualmente, come già detto, non esiste un algoritmo di complessità polinomiale che, dato un
naturale n>1 in input, calcoli i suoi fattori primi.
Potrebbe naturalmente essere trovato un algoritmo di complessità polinomiale che, dato un naturale
n>1 in input, calcoli la funzione di Eulero (n), senza calcolare i fattori primi di n: tuttavia a
tutt’oggi non esiste un algoritmo di questo tipo.
Anzi molti matematici sono convinti che sia vera la seguente
Congettura: Per un input intero n>1 il problema della fattorizzazione di n in prodotto di primi e del
calcolo della funzione di Eulero (n) sono equivalenti da un punto di vista algoritmico.
Ad avvalorare tale congettura, si può notare che in alcuni casi particolari dalla conoscenza di (n) si
può risalire al calcolo dei fattori primi di n: per esempio se n=pq, con p,q primi distinti, allora
conoscendo (n)=(p-1)(q-1)=pq-(p+q)+1, è possibile calcolare anche p+q=pq-(n)+1=n-(n)+1, da
cui, impostando un classico sistema somma-prodotto:
pq n
p q n - (n) 1
è possibile ricavare i valori dei fattori p, q (come soluzioni di un’equazione di secondo grado).
Una situazione di questo tipo, come vedremo, si verifica nel sistema crittografico RSA.
Il seguente risultato (che dimostreremo nella prossima lezione) permette di ricondurre il calcolo di
(n) al calcolo dei (d) con d<n:
Teorema.
Per ogni naturale n>1 si ha n=
(d )
d n
1 d n
(e in particolare (n)=n -
(d ) )
d n
1 d n