EQUILIBRIO DI MONOPOLIO
L’obiettivo del monopolista è massimizzare il profitto, ossia
MAX = TR(Q) – TC(Q)
Ricordiamo che massimizzare una funzione (in questo caso ci occupiamo della funzione
di profitto!) significa trovarne il punto di massimo ponendo la derivata prima della
funzione considerata uguale a zero.
Ricordando le definizioni di ricavo marginale e di costo marginale, arriviamo alla regola
che ci permette di trovare l’equilibrio di monopolio:
TR TC
0
Q Q Q
MR = MC
Il che, in pratica, significa che:
-
porre MR = MC ci permette di trovare la quantità di equilibrio Q*.
-
mentre per trovare il prezzo di equilibrio p* dobbiamo sostituire Q* nella
curva di domanda (e non nella curva dei ricavi marginali, attenzione!).
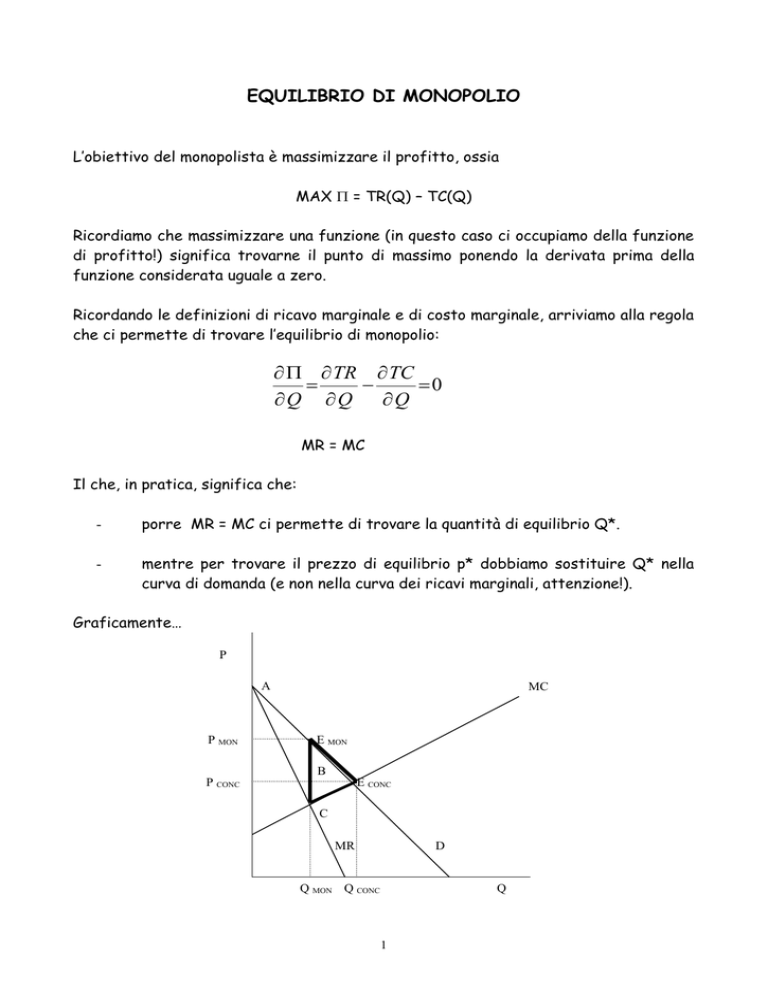
Graficamente…
P
A
P MON
MC
E MON
B
P CONC
E CONC
C
MR
D
Q MON Q CONC
Q
1
Il grafico sovrastante mostra che, in equilibrio:
-
la quantità prodotta è inferiore a quella che sarebbe prodotta in equilibrio in
concorrenza perfetta
-
il prezzo è superiore a quello che si avrebbe in concorrenza perfetta.
Produrre una quantità più bassa ad un prezzo più alto rappresenta una perdita di
benessere per la collettività. Graficamente, tale perdita (detta “perdita netta” di
monopolio) è rappresentata dal triangolo evidenziato.
Nel passaggio da una situazione di concorrenza perfetta (punto ECONC) ad una
situazione di monopolio (punto EMON), si ha una variazione di surplus sia del
consumatore sia del produttore:
- il sovrappiù del consumatore si riduce: in concorrenza perfetta, tale sovrappiù era
rappresentato dall’area del triangolo ApconcEconc; in monopolio, il triangolo che
rappresenta tale sovrappiù è ApmonEmon, che è più piccolo!
Quindi variazione del surplus del consumatore: - area trapezio pmonEmonEconcpconc
- per quanto riguarda il surplus del produttore: il rettangolo pmonEmonBpconc
rappresenta un aumento del suo surplus (aumenta il prezzo da pconc a pmon per tutte le
unità che già vendeva fino a qm e quindi il monopolista si appropria di una parte del
sovrappiù del consumatore), mentre il triangolo BEconcC rappresenta una riduzione del
suo surplus (perdita derivante dalla minor vendita: si passa da qc a qm)
Quindi variazione del surplus del produttore: area rettangolo pmonEmonBpconc – area
triangolo BEconcC
- Variazione di surplus totale: -area triangolo EmonEconcC
Quindi, in seguito alla diminuzione della quantità prodotta, e di un prezzo più elevato,
una parte della produzione non viene realizzata e non può essere appropriata, in
termini di surplus, né dal produttore né dal consumatore!
2
L’unico modo affinché non vi sia la perdita netta di monopolio è che il monopolista
pratichi la discriminazione di prezzo perfetta o del prim’ordine, ossia sia in grado di
far pagare a ciascun consumatore il prezzo massimo che egli è disposto a pagare per il
bene considerato. In questo caso, il sovrappiù del consumatore è nullo (è zero la
differenza tra quanto sarebbe disposto a pagare e quanto paga!) e il monopolista si
appropria di tutto il sovrappiù del consumatore, producendo una quantità pari alla
quantità di equilibrio di concorrenza perfetta.
3
SCELTE IN CONDIZIONI DI INCERTEZZA
VALORE
ATTESO
=
VALORE
MEDIO
ASSUNTO
DALLA
VARIABILE
CONSIDERATA TENENDO CONTO DEI POSSIBILI ESITI DELLA SCOMMESSA
EV = p1 X1 + p2 X2 +…. Pn Xn
dove Xi sono i possibili esiti della scommessa e pi sono le probabilità che tali esiti si
realizzino
UTILITA’
ATTESA
=
UTILITA’
MEDIA
OTTENUTA
DALL’INDIVIDUO
TENENDO CONTO DEI POSSIBILI ESITI DELLA SCOMMESSA
EU = p1 U ( M1 ) + p2 U ( M2 )+…. Pn U ( Mn )
dove Mi è la ricchezza complessiva di cui l’individuo dispone per effetto dei possibili
esiti della scommessa e pi sono le probabilità che tali esiti si realizzino
LA FORMA DI TALE FUNZIONE DI UTILITA’ DIPENDE (COME SEMPRE) DALLE
PREFERENZE DELL’INDIVIDUO, CHE PUO’ ESSERE:
-
AVVERSO AL RISCHIO
-
PROPENSO AL RISCHIO
-
NEUTRALE AL RISCHIO
4
1°caso: AVVERSIONE AL RISCHIO
A PARITA’ DI RICCHEZZA ATTESA, L’INDIVIDUO PREFERISCE:
-
(se deve scegliere se scommettere o no)
RINUNCIARE ALLA POSSIBILITA’ DI AUMENTARE IL PROPRIO DENARO
PARTECIPANDO ALLA SCOMMESSA PUR DI NON SOSTENERE IL RISCHIO
DI PERDERLA
-
(se deve scegliere se assicurarsi o no)
AVERE MENO DENARO – OSSIA PAGARE UN PREMIO
–
PUR DI NON
SOSTENERE IL RISCHIO DI UN EVENTO NEGATIVO.
LA SUA FUNZIONE DI UTILITA’ SARA’ DEL TIPO:
U (M) = M CON
< 1
OSSIA SARA’ UNA FUNZIONE CONCAVA rispetto alla ricchezza totale M
U (M2)
EU
U (M1)
Premio max che individuo è
disposto a pagare per evitare rischio
di evento sfavorevole = valore max EC
M1
EC EM
M2
5
2°caso: PROPENSIONE AL RISCHIO
A PARITA’ DI RICCHEZZA ATTESA, L’INDIVIDUO PREFERISCE:
-
(se deve scegliere se scommettere o no)
SOSTENERE IL RISCHIO DI PERDERE LA SCOMMESSA PUR DI AVERE LA
POSSIBILITA’ DI AUMENTARE IL PROPRIO DENARO PARTECIPANDO AD
ESSA.
-
(se deve scegliere se assicurarsi o no)
SOSTENERE IL RISCHIO DI UN EVENTO NEGATIVO PUR DI NON VEDERE
DIMINUIRE IL PROPRIO DENARO MEDIANTE IL PAGAMENTO DEL
PREMIO.
LA SUA FUNZIONE DI UTILITA’ SARA’ DEL TIPO:
U (M) =M CON
> 1
OSSIA SARA’ UNA FUNZIONE CONVESSA rispetto alla ricchezza totale M
U (M2)
Premio max che individuo è
disposto a pagare per evitare rischio
di evento sfavorevole = valore max EC
EU
U (M1)
M1
EM EC
EC
M2
6
3°caso:
NEUTRALITA’ AL RISCHIO
A PARITA’ DI RICCHEZZA ATTESA, L’INDIVIDUO E’ INDIFFERENTE TRA:
-
(se deve scegliere se scommettere o no)
MANTENERE INVARIATA LA PROPRIA QUANTITA’ DI DENARO NON
SCOMMETTENDO E VEDERLA
AUMENTARE SOSTENENDO IL RISCHIO
DELLA SCOMMESSA
-
(se deve scegliere se assicurarsi o no)
ASSICURARSI RINUNCIANDO AD UNA QUANTITA’ DI DENARO PARI AL
PREMIO E NON ASSICURARSI SOSTENENDO IL RISCHIO CHE SI
VERIFICHI UN EVENTO NEGATIVO
LA SUA FUNZIONE DI UTILITA’ SARA’ DEL TIPO:
U (M) = M CON
= 1
OSSIA SARA’ UNA FUNZIONE LINEARE rispetto alla ricchezza totale M
U (M2)
EU
Premio max che individuo è
disposto a pagare per evitare rischio
di evento sfavorevole = valore max EC
U (M1)
M1
EC = EM
M2
7
EQUIVALENTE CERTO (E.C.) DI UNA SCOMMESSA:
DEFINIZIONE
E’ L’AMMONTARE DI DENARO CERTO CHE CONFERISCE ALL’INDIVIDUO LA
STESSA UTILITA’ DELLA SCOMMESSA CONSIDERATA.
INTERPRETAZIONE GEOMETRICA
E’ RAPPRESENTATO DALL’ASCISSA DEL PUNTO SULLA FUNZIONE DI UTILITA’
U(M) AVENTE PER ORDINATA L’UTILITA’ ATTESA DELLA SCOMMESSA.
CALCOLO DELL’EQUIVALENTE CERTO DI UNA SCOMMESSA
SE LA FUNZIONE DI UTILITA’ E’
U (M) = M
E L’UTILITA’ ATTESA DELLA SCOMMESSA E’ PARI A U* (cioè è data da un valore
numerico che ho precedentemente calcolato o mi viene dato dall’esercizio)
L’EQUIVALENTE CERTO della scommessa SARA’ DATO DA:
M = (U*)
-
1/
SE L’INDIVIDUO E’ AVVERSO AL RISCHIO L’E.C. SI TROVA A SINISTRA
DELLA RICCHEZZA ATTESA DELLA SCOMMESSA
-
SE L’INDIVIDUO E’ PROPENSO AL RISCHIO L’E.C. SI TROVA A DESTRA
DELLA RICCHEZZA ATTESA DELLA SCOMMESSA
-
SE L’INDIVIDUO E’ NEUTRALE AL RISCHIO L’E.C COINCIDE CON LA
RICCHEZZA ATTESA DELLA SCOMMESSA
8
QUANDO MI SERVE L’EQUIVALENTE CERTO?
QUANDO DEVO STABILIRE SE UN INDIVIDUO SCEGLIE SE ASSICURARSI O
NO: CONFRONTO IL PREMIO DELL’ASSICURAZIONE CON LA DIFFERENZA TRA
VALORE MASSIMO ED EQUIVALENTE CERTO.
INFATTI:
IL prezzo MASSIMO CHE L’INDIVIDUO E’ DISPOSTO A PAGARE (SOTTOFORMA
DI PREMIO AL RISCHIO) PUR DI EVITARE IL RISCHIO DI SUBIRE UN EVENTO
ALEATORIO
SFAVOREVOLE
E’
DATO
DALLA
DIFFERENZA
TRA
VALORE
MASSIMO ED EQUIVALENTE CERTO!
-
SE L’INDIVIDUO E’ AVVERSO AL RISCHIO, SCEGLIERA’ DI ASSICURARSI
COMPLETAMENTE SE:
premio < valore massimo – E.C.
9
ESTERNALITA’
Si parla di esternalità negativa (o positiva) di produzione quando i costi dell’impresa A
aumentano (o, rispettivamente, diminuiscono) come conseguenza dell’attività
dell’impresa B senza che i prezzi di mercato tengano conto di tale effetto, cioè:
-
se qA aumenta CTB aumenta, allora ho esternalità negativa di A nei confronti di B
-
se qA aumenta CTB diminuisce, allora ho esternalità positiva di A nei confronti di
B
Se le imprese A e B agiscono in modo indipendente, si procede nel modo consueto,
ossia massimizzando il profitto rispetto alla/e variabile/i di scelta (di solito si tratta
della quantità da produrre) dell’impresa considerata separatamente per entrambe le
imprese.
Si ha, quindi:
Pr ofittoA
0
qA
Pr ofittoB
0
qB
(che equivale ad applicare la regola MRA = MC A ed MRB = MC B)
In questo caso (e, cioè, se le due imprese operano separatamente), la scelta ottima
che ciascuna compie è efficiente a livello privato; tuttavia, essa non coincide con la
scelta socialmente ottima.
Se le imprese A e B agiscono in modo congiunto, invece, si massimizza il
CONGIUNTO
(Profittototale = ProfittoA + ProfittoB)
delle due imprese rispetto a
TUTTE
le variabili di scelta e cioè:
10
PROFITTO
Pr ofittototale
0
qA
Pr ofittototale
0
qB
N.B. Il numero di equazioni che compongono il sistema sarà pari al numero di variabili
rispetto alle quali l’impresa risultante dalla fusione può scegliere.
11
ASIMMETRIA INFORMATIVA
La disponibilità a pagare di un soggetto che non dispone di informazione completa sul
bene (ossia non sa se il bene è “buono” o “cattivo” prima di averlo acquistato) coincide
con il valore atteso del prezzo attribuito al bene, e cioè:
PD = E(p) = probabilitàbuono * prezzobuono + probabilitàcattivo * prezzocattivo
Il mercato del bene “buono” scompare solo se:
PD < PSbuono, a cui i venditori sono disposti ad offrire il bene buono (che possiamo
considerare come costo marginale)
Questo è il caso in cui si verifica la cosiddetta SELEZIONE AVVERSA.
Se, invece, si ha che
PD > PSbuono > PScattivo
allora entrambi i beni verranno venduti sul mercato.
12