Filtro RC passa-basso

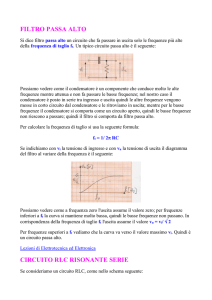
I Filtri di Frequenza
Filtri passivi RC
I filtri di frequenza (o semplicemente Filtri) sono dei dispositivi atti a selezionare i segnali in funzione della
loro frequenza.
Chiamiamo
A0 
vu
l’attenuazione subita dal segnale nell’attraversare il Filtro, con ve il segnale applicato
ve
all’ingresso (segnale di entrata) e vu il segnale prelevato all’uscita del Filtro.
Si hanno i seguenti quattro tipi di filtri:
1. Filtri passa-basso PB: questi Filtri hanno A0 ≠ 0 solo per i segnali di ingresso a frequenze inferiori
ad un determinato valore di ft, chiamata frequenza di taglio superiore. Per f > ft si ha invece A0 = 0.
2. Filtri passa-alto PA: questi Filtri hanno A0 ≠ 0 solo per i segnali di ingresso a frequenze superiori ad
un determinato valore di ft, chiamata frequenza di taglio inferiore. Per f < ft si ha invece A0 = 0.
3. Filtri passa-banda Pbanda: questi Filtri hanno A0 ≠ 0 solo per i segnali di ingresso la cui frequenza
è interna a due determinati valori f1 (chiamata frequenza di taglio inferiore) ed f2 (chiamata frequenza
di taglio superiore) con f1 < f2. Per f < f1 e f > f2 si ha invece A0 = 0.
4. Filtri elimina-banda Ebanda: questi Filtri hanno A0 ≠ 0 solo per i segnali di ingresso la cui frequenza
è esterna a due determinati valori f1 (chiamata frequenza di taglio inferiore) ed f2 (chiamata
frequenza di taglio superiore) con f1 < f2. Per f1 < f < f2 si ha invece A0 = 0.
Filtro
ve
vu
f
A
A
ft
f
A
f
ft
A
f1
f2
f
f1
f2
f
In figura sono riportate le curve di risposta dei Filtri rispettivamente passa-basso, passa-alto, passabanda e elimina-banda. I fronti ripidi di discesa e salita sono puramente ideali. In pratica le curve si
discostano da quelle sopra riportate e la bontà di un filtro è tanto maggiore quanto più esso approssima le
curve ideali.
I Filtri si dividono in:
a) Filtri passivi: se sono composti da soli componenti passivi
b) Filtri attivi: se sono compresi anche componenti attivi, BJT, FET e Operazionali.
Studieremo innanzitutto i Filtri passivi.
Filtro RC passa-basso
R
R
Vu
Ve
C
Come si può osservare dalla figura la tensione di uscita V u viene prelevata ai capi di C.
La caratteristica del filtro passa-basso è quella di privilegiare la trasmissione delle frequenze basse, infatti
dalla figura si ricava che:
1
1
Ve
jC
Vu 

1
1  jRC
R
jC
Ve
Il modulo di A0 vale:
A0 
e la fase:
Vu
1

Ve
1  (RC ) 2
  arctg (RC )
Dal modulo si ricava che per frequenze basse e tali che 2 π f R C « 1, il rapporto V u / Ve rimane
sensibilmente costante e uguale a 1 (cioè l’uscita è uguale in ampiezza all’ingresso), ma non appena la
frequenza aumenta in modo tale che la quantità 2 π f R C incomincia ad assumere valori non trascurabili
rispetto l’unità, il rapporto Vu / Ve incomincia a decrescere. I limiti sono i seguenti: per f = 0 è Vu = Ve, per f
→ ∞ è Vu = 0.
Vu/Ve
A0 
1
1/√2
Vu
1

Ve
1  (RC ) 2
ft
Curva di risposta dell’ampiezza del Filtro Passa-Basso
ft
f
f
φ
-45°
-90°
Curva di risposta delle Fasi del Filtro Passa-Basso
Quindi se un segnale di ingresso ha frequenza variabile il circuito RC di figura fa passare le frequenze basse
e taglia quelle alte, cioè si comporta da filtro passa-basso. In altre parole, prelevando l’uscita ai capi di C, si
ha una risposta Vu = Ve e φ = 0 per frequenze basse tali che
2 π f R C « 1, mentre per frequenze man
mano crescenti, la tensione di uscita si riduce in ampiezza fino a quasi annullarsi, mentre si va generando un
ritardo di fase di Vu rispetto Ve, che da 0° va crescendo fino a –90°. Dalle formule si ricavano i grafici sopra
riportati che prendono il nome di Curva di risposta del filtro Passa-Basso.
La frequenza più alta, che rappresenta il limite massimo in corrispondenza del quale l’attenuazione della
tensione di uscita rispetto alla tensione di ingresso si può ritenere trascurabile, viene chiamata frequenza di
taglio superore e si indica con ft. Essa viene definita come la frequenza in corrispondenza della quale è:
Vu 
Ve
2
 0,707 Ve
Per ricavare ft basta imporre nell’equazione del modulo di A0 sia:
2
Vu
1
1


2
Ve
2
1  (RC )
e cioè:
(RC ) 2  1
da cui si ricava la frequenza di taglio superiore:
ft 
1
2RC
In pratica i dispositivi di filtraggio vanno interposti fra una sorgente, simulabile con un generatore di tensione
a frequenza variabile avente in serie la resistenza interna Ri, ed un carico utilizzatore Rc.
Il dimensionamento del filtro si effettua imponendo che:
R >> Ri
Rc >> R + Ri
E’ sufficiente in pratica che sia:
R = 10 Ri
Rc = 10 R
R
Rc
Ri
Vu
Ve
C
Filtro Passa-Basso
Filtro RC passa-alto
Vu
Ve
C
R
Si consideri adesso il circuito RC di figura nel quale la tensione di uscita viene prelevata ai capi di R. Si
dimostra che questa configurazione del circuito RC privilegia la trasmissione delle alte frequenze.
R
Vu  Ve
R
1
jC
 Ve
jRC
1  jRC
Il modulo di A0 vale:
Vu
(RC ) 2

Ve
1  (RC ) 2
e la fase:
  90 0  arctg (RC )
3
Vu
(RC ) 2

Ve
1  (RC ) 2
A0
1
1/√2
ft
Curva di risposta dell’ampiezza del Filtro Passa-Alto
f
φ
90°
45°
00
ft
f
Curva di risposta delle Fasi del Filtro Passa-Alto
I valori limiti della funzione modulo sono:
Vu / Ve = 0 per f → 0
Vu / Ve = 1 per f → ∞
Cioè il filtro taglia le basse frequenze e fa passare solo quelle alte, comportandosi quindi come un filtro
Passa-Alto.
Si definisce frequenza di taglio inferiore quella frequenza che rende il modulo
Vu 
Ve
2
 0,707 Ve , cioè
quella frequenza per cui:
(RC ) 2  1
da cui:
ft 
1
2RC
Come per il Filtro Passa-Basso, anche per il Filtro Passa-Alto in genere si usa come dispositivo intercalato
tra una sorgente di segnale ve e un carico Rc
C
Ve
R
Filtro Passa-Alto
Il dimensionamento del filtro si effettua imponendo che:
4
Rc
Vu
Ri
R >> Ri
Rc >> R
E’ sufficiente in pratica che sia:
R = 10 Ri
Rc = 10 R
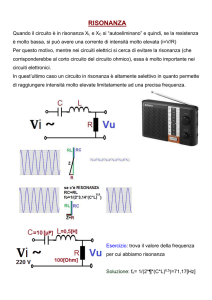
Circuiti risonanti
La risonanza può avvenire nei circuiti contenenti reattanze induttive e capacitive. La sua caratteristica è che
ad una determinata frequenza, chiamata frequenza di risonanza, l’impedenza del circuito è puramente
resistiva. Di conseguenza lo sfasamento tra la tensione applicata e corrente di ingresso è zero. Si hanno due
tipi di risonanza:
1. risonanza serie quando l’impedenza di ingresso (resistiva) è minima alla frequenza di risonanza;
2. risonanza parallelo quando l’impedenza di ingresso (resistiva) è massima alla frequenza di
risonanza.
Risonanza serie
Quando la reattanza capacitiva è in serie a quella induttiva si ha un circuito risonante serie come in figura.
Vu
Ve
C
R
L
L’impedenza del circuito vale:
Z  R
1
1
 jL  R  j (L 
)
jC
C
Il modulo dell’impedenza vale:
Z  R 2  (L 
1 2
)
C
Nel circuito circolerà la corrente data dalla:
Ve
I
R  j (L 
1
)
C
Se analizziamo il modulo dell’impedenza notiamo che essa diventa mima e completamente resistiva quando:
0L 
e vale
1
 0C
Z0  R
cioè a quella frequenza
f0 
1
2 LC
che viene chiamata frequenza di risonanza. In corrispondenza di questa frequenza nel circuito circola la
massima corrente
I0 
Ve
.
R
Per frequenze inferiori o superiori a f 0 il circuito è reattivo, e precisamente:
5
 per ω < ω0 comportamento capacitivo
 per ω > ω0 comportamento induttivo
Lo sfasamento tra la tensione e la corrente che circola nel circuito è:
  arctg (
L 
R
1
C )
Alla risonanza si ha quindi:
 0
C’è un intorno della frequenza f 0 dentro il quale l’impedenza si può ritenere resistiva e quasi costante.
Questo intorno è limitato superiormente da una frequenza f 2 chiamata frequenza di taglio superiore, e
inferiormente da un frequenza f 1 chiamata frequenza di taglio inferiore. A queste due frequenze
corrisponde una attenuazione della I0 del fattore 0,707 e uno sfasamento di  45 °. L’intervallo B = f2 – f1 è
chiamata Banda passante.
Si hanno le seguenti relazioni:
B
2
B
f2  f0 
2
f2  f0 
Nelle figure successive vengono rappresentate le curve caratteristiche del circuito risonante serie chiamate
curve di risonanza.
capacitivo
resistivo
induttivo
I
I0
I0/√2
B
f1
f0
f2
f
f1
f0
f2
f
φ
90°
45°
0°
-45°
-90°
Un’altra caratteristica del circuito di risonante è il coefficiente di risonanza ε, il quale caratterizza la
selettività del circuito stesso. Sussiste la seguente relazione:

6
f0
B
Infatti quanto più piccola è la banda passante B tanto più selettivo è il circuito nei confronti delle frequenze
presenti all’ingresso del circuito, e tanto più alto e ε.
Il valore di ε è dato pure dal rapporto fra la reattanza, alla frequenza di risonanza, e la resistenza serie
presente nel circuito:

0 L
R

1
 0 CR
Quanto più è prevalente la reattanza sulla Rs, tanto più alto è ε e quindi tanto più selettivo è il circuito; ε
viene chiamato anche coefficiente di sovratensione.In fatti la tensione ai capi di L e C alla risonanza vale:
Ve
 jVe
R
I
1 Ve
VC  0 
  jVe
j 0 C j 0 C R
VL  j 0 LI 0  j 0 L
Cioè alla risonanza le due tensioni VL e VC sono sfasate di 90° in anticipo e in ritardo rispetto alla tensione V0
applicata e la loro ampiezza ha un valore ε volte maggiore della V0 applicata.
Risonanza parallelo
R
C
L
Vu
I
La configurazione del circuito risonante parallelo è quello della figura successiva. Come si vede è alimentato
da un generatore di corrente I.
La tensione Vu di uscita è funzione della frequenza del segnale applicato all’ingresso, secondo la legge:
Vu 
I
I

1
Y 1
 j (C 
)
R
L
Si ha la risonanza parallelo e l’impedenza Z
Z
1
1

1
Y 1
 j (C 
)
R
L
Il modulo dell’impedenza vale:
Z 
Assume il suo massimo valore per
1
1
1 2
 (C 
)
2
L
R
Z 0  R per quella particolare frequenza, chiamata frequenza di
risonanza, per cui:
 0C 
1
0L
cioè alla frequenza:
f0 
1
2 LC
Come si vede dall’equazione dell’impedenza, per frequenze diverse da f0 le caratteristiche del circuito sono:
7
 comportamento induttivo per ω < ω0
 comportamento capacitivo per ω > ω0
L’equazione che rappresenta la curva delle fasi è:
  arctg (
C 
alla risonanza è φ = 0, alle frequenze di taglio è φ = ± 45°
induttivo
1
R
1
L )
resistivo
capacitivo
V
V0
V0/√2
B
f1
f0
f2
f
f1
f0
f2
f
φ
90°
45°
0°
-45°
-90°
Le definizioni sono le stesse date per il circuito risonante serie.
Il coefficiente di risonanza vale:
   0 CR 
R
0L
e vale sempre la relazione:

f0
B
Il coefficiente ε viene chiamato (per i circuiti risonanti parallelo) “coefficiente di sovracorrente”. Infatti la
corrente che passa in L e C alla risonanza vale:
I0R
  jI 0
j 0 L j 0 L
I C  j 0 CVu  j 0 CRI 0  jI 0
IL 
Vu

Cioè ciascuna corrente reattiva è ε volte la corrente del generatore.
8