Circuito passa-banda RLC parallelo
Scopo dell’esperienza
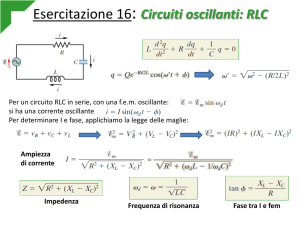
Il circuito RLC parallelo ai capi del parallelo LC si comporta in corrente alternata come un
filtro bassa-banda caratterizzato da due grandezze: la frequenza di risonanza ed il fattore di
merito, che dà una misura della larghezza della banda passante. In questo circuito il modulo
della funzione di trasferimento A e la sua fase ϕ = arg ( A) sono definito in regime
sinusoidale come:
A≡
Vout
=
Vin
1
2
2
⎛ R ⎞
2
1+ ⎜
⎟ (ω LC − 1)
⎝ ωL ⎠
⎡ R
⎤
ω 2 LC − 1) ⎥
(
⎣ωL
⎦
ϕ = − arctan ⎢
si determinino sia la pulsazione di risonanza ω0 per cui A =1:
ω0 =
1
LC
che il fattore di merito alla risonanza Q0 definito come:
Q0 =
ω0
L
= ω0
R
ω1 − ω2
dove ω1 ed ω2 sono i punti in cui A vale 1
Materiali principali
1.
Cassetta di base
2.
Due tester
3.
Una resistenza nota
4.
Una capacità nota
5.
Un’induttanza nota
6.
Oscilloscopio
2.
Procedura
■ Scegliere i valori dell’induttanza e della capacità affinché la frequenza di taglio sia
compresa tra 1 e 10 kHz e scegliere la resistenza in modo che il fattore di merito sia compreso
tra 0,5 e 1.
■ Misurare la resistenza, la capacità e l’induttanza.
■ Calcolare la pulsazione di taglio ω0, la frequenza di taglio ν 0 =
ω0
e il fattore di merito Q0.
2π
■ Misurare alcuni valori della tensione di ingresso e ai capi della resistenza ed utilizzando
l’oscilloscopio misurare il periodo e da questo ricavarsi la pulsazione.
■ Mettere i dati in una tabella con le relative indeterminazioni.
■ Calcolare la funzione di trasferimento
A
e la fase ϕ = arg ( A) con relative
indeterminazioni.
■ Disegnare in un grafico l’andamento delle precedenti grandezze in funzione della
pulsazione.
■ Ricavare L e C dai valori misurati di ω0 e Q0 e confrontarli con quelli nominali, discutere
eventuali discrepanze.
■ Discutere i risultati ottenuti.