2 esercitazione2

Alunno : Lamacchia Cosimo
Classe : 5^ A inf
Data consegna : 12/12/2007
OGGETTO: Progettazione, sperimentazione e simulazione di circuiti elettronici
con OP-AMP 741
Fase 1: Verifica dell’amplificatore sommatore invertente
Fase 2: Verifica del comparatore Trigger di Schmitt invertente
Fase 3: Verifica del circuito integratore e derivatore
INTRODUZIONE
 Sommatore realizzato con OP-AMP
L’amplificatore sommatore è un dispositivo realizzato con una serie di resistenze e un OP-AMP,
ed è in grado di sommare delle tensioni in ingresso.
Come nel caso di amplificatori e comparatori, ne esistono di due tipi:
o Sommatore invertente
o Sommatore non invertente
o Sommatore algebrico
► Sommatore invertente
Il sommatore invertente è realizzato collegando l’ingresso non invertente a massa, mentre
all’ingresso invertente vengono collegate le tensioni in esame da sommare. Ovviamente in uscita si
avrà una tensione amplificata e inversa.
V1
R4
R1
I1
V2
I4
R2
[esempio di amplificatore sommatore
invertente]
I2
OP-AMP
V3
VU
R3
I3
La figura riporta un esempio di sommatore invertente, in cui si richiede la somma delle tensioni in
ingresso, quindi tendo presente anche del guadagno di ogni tensione ed essendo invertente il
segnale in uscita sarà:
n
VU   AiVi
i 1
nel caso in esempio ci sono 3 tensioni in ingresso (V1,V2,V3), quindi:
VU  ( A1V1  A2V2  A3V3 )
La verifica del circuito si può ricavare tramite applicazione del:
- 1° principio di Kirchoff
RV RV
RV 
V
V
V V
I4 = I1 + I2 + I3
→
→
VU   4 1  4 2  4 3 
 U  1  2  3
R2
R3 
R4 R1 R2 R3
 R1
I guadagni saranno:
R
R
R
A1   4
A2   4
A3   4
R1
R2
R3
- Principio di sovrapposizione degli effetti
In questo caso si fa agire un segnale per volta mettendo a massa le resistenze non prese in
esame. In tal caso si avrà:
RV RV
RV 
VU  VUI  VUII  VUIII   4 1  4 2  4 3 
R2
R3 
 R1
-1-
► Sommatore non invertente
Realizzato applicando all’ingresso non invertente le tensioni da esaminare, mentre l’ingresso
invertente è posto a massa, per non avere un guadagno infinito si applica la rete e retroazione
negativa. In uscita si avrà un segnale amplificato che conterrà la somma dei segnali in ingresso.
R5
R4
OP-AMP
V1
V2
V3
VU
R1
[esempio di amplificatore sommatore
invertente]
R2
R3
Il segnale in uscita sarà determinato dalla somma delle tensioni in ingresso, anche in questo caso
influenzata dal guadagno di ogni segnale, tenendo presente che è un amplificatore non invertente:
n
VU   AiVi
i 1
nel caso in esempio ci sono 3 tensioni in ingresso (V1,V2,V3), quindi:
VU  A1V1  A2V2  A3V3
Il valore del segnale in uscita lo si può ricavare applicando il principio di sovrapposizione degli
effetti.
VU  VUI  VUII  VUIII
Facendo agire un solo segnale per volta, quindi collegando i segnali non presi in esame a massa, si
forma un parallelo tra due resistenze e trovata la resistenza equivalente si può applicare il partitore
di tensione:
R2 , 3 
R1,3 
R1, 2 



R 
R 
R 
II
I



1  5 V2
1  5 V3
VUI  1  5 V1
V

V

U
U
R4  R2,3  R1 
R4  R1,3  R2 
R4  R1, 2  R3 



In questo caso l’uscita assumerà il seguente valore:
R2 , 3  
R1,3  
R2,1 

R 
   V2
  V3

VU  1  5 V1
  R R   R R 
R
R

R
4 
2,3
1 
1, 3
2 
2 ,1
3 



Da qui si nota che i guadagni di ogni segnale saranno influenzati anche dalla rete a reazione
negativa.



R  R2,3 
R  R1,3 
R  R1, 2 



1  5 
1  5 
A1  1  5 
A

A

2
3

R R 
R R 
R
R

R
R
R
4  2 , 3
1 
4  1, 3
2 
4  1, 2
3 



► Sommatore algebrico
Questo tipo di sommatore è in grado di effettuare la somma algebrica tra più segnali, taluni applicati
all’ingresso non invertente, altri applicati all’ingresso invertente.
-2-
 Comparatore Trigger di Schmitt
Comparatore trigger di Schmitt, chiamato anche comparatore con isteresi, è un comparatore a cui è
stata aggiunta una rete resistiva a reazione positiva.
Vi
VU
OP-AMP
[ comparatore trigger di Schmitt invertente]
R2
I
VRif
R1
Questo tipo di comparatore ha le stesse applicazioni del comparatore semplice, ma solitamente è
utilizzato in situazioni in cui si richiede maggiore sicurezza e immunità riguardo hai disturbi.
Tale sicurezza è data dal fatto che la rete resistiva porta ad avere in uscita il cambiamento di stato
logico solo nel caso in cui si raggiunge il segnale in ingresso raggiunge una determinata tensione di
riferimento e la particolarità che questa tensione è differente nei due momenti in cui il segnale passa
da un valore di picco all’altro.
Nel caso di un Trigger di Schmitt invertente il segnale in ingresso Vi viene collegato all’ingresso
invertente e il valore della tensione di riferimento è determinato dalle 2 resistenze che formano la
rete, e può essere calcolato nel seguente modo:
V Rif  R1  I
applicando la formula del partitore di tensione avremo:
R1
VRif 
* VU
R1  R2
Essendo un comparatore l’uscita ( VU ) sarà un segnale a due livelli quindi potrà assumere solo i
valori +VSat e –VSat(tensione di saturazione), quindi la VRif potrà variare tra due tensioni, indicate
con VT+ e VT- :
R1
VT   VSat
R1  R2
VRif
R1
u
VT   VSat
R1  R2
+VSat
[curva di trasferimento del comparatore TS invertente]
VT-
VT+
O
-VSat
Vi
Dalla curva di trasferimento si può notare come
l’uscita cambia stato logico non appena la Vi
raggiunge una delle soglie di riferimento.
Precisamente Vu assumerà valore +VSat finché la Vi
sarà minore di VT+. Raggiunta tale soglia la Vu
assumerà valore –VSat finché la Vi sarà maggiore di
VT-3-
Nel caso in cui il comparatore trigger di Schmitt sia non invertente il segnale in ingresso Vi è
collegato all’ingresso non invertente, mentre l’altro ingresso viene posto a massa.
VU
OP-AMP
[ comparatore trigger di Schmitt non invertente]
R2
I
VRif
R1
Vi
Il funzionamento è identico al comparatore invertente solo la VRif assumerà valori differenti.
R1
R2
VRif 
*VU 
*Vi
R1  R2
R1  R2
Tenendo presente che Vu assumerà solo valori pari a –VSat e +VSat, i du valori di VRif saranno:
R1
R2
VT   VSat
 Vi
R1  R2
R1  R2
VRif
R1
R2
VT   VSat
 Vi
R1  R2
R1  R2
u
+VSat
[curva di trasferiemto comparatore TS non invertente]
VT-
VT+
O
Vi
Allo stesso modo delll’invertente, l’uscita di questo
comparatore TS cambia stato logico non appena la
Vi raggiunge una delle soglie di riferimento. In
questo caso la Vu avrà valore –VSat finché la Vi non
raggiunge il valore VT+, mentre avrà valore +VSat
finché la Vi non raggiunge il valore VT-.
-VSat
-4-
 Derivatore
Il circuito derivatore è un circuito che genera la derivata di ogni segnale in ingresso
R
IR
C
Vi
IC
[Circuito derivatore]
VU
OP-AMP
Come si può vedere nella figura, il derivatore è realizzato mediante l’utilizzo di un OP-AMP,a cui
viene aggiunta una rete RC, come rete a retroazione.
Il circuito è in grado di generare la derivata del segnale, in quanto il grazie al condensatore viene
generata una corrente che varia in funzione della quantità di carica e del tempo.
dQ C * dVi

dt
dt
[ dVi e dt rappresentano le variazioni di tensione e tempo]
IC 
Sulla resistenza passa un’altra corrente
IR  
Vu
R
Dato che il punto M è un punto di massa virtuale, perchè i due ingressi del OP-AMP hanno lo
stesso potenziale, le due correnti sono uguali, quindi potremo scrivere:
IC  I R
→
C  dVi
Vu

dt
R
A questo punto si può ricavare il valore del segnale in uscita:
Vu   RC
dVi
dt
-5-
 Integratore
Il circuito integratore è in grado di generare l’integrale del segnale in ingresso.
C
IC
Vi
R
[Circuito integratore]
IR
VU
OP-AMP
L’integratore è realizzato con un OP-AMP a cui, come nel derivatore, è stata collegata una rete RC
a retroazione, ma la contrario del derivatore, come si può vedere in figura, si invertono le posizioni
della resistenza e del condensatore.
Anche in questo caso le correnti che passano sulla resistenza R e sul condensatore C sono uguali,
dato che anche in questo caso c’è un punto di massa virtuale.
Quindi avremo:
IC 
dQ
C * dVu

dt
dt
IC  I R
IR 

→
Vi
R
C  dVu Vi

dt
R
Da cui si può ricavare la tensione in uscita che sarà:
Vu  
1
Vi  t
RC 
-6-
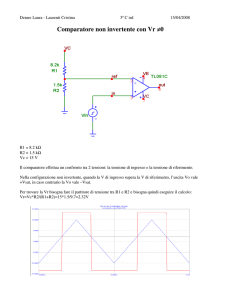
FASE 1:
VERIFICA DELL’AMPLIFICATORE SOMMATORE INVERTENTE
L’esercitazione richiede l’utilizzo di un sommatore invertente che, sommando due segnali, converta
un segnale triangolare alternativo di 0,2 V da picco a picco (VPP),ovvero il segnale Vi, in un
segnale triangolare unipolare positivo di 2 VPP. Pertanto bisogna generare un guadagno pari a 10,
quindi determinare il valore, delle tre resistenze da utilizzare e del secondo segnale (VX).
L’OP-AMP utilizzato per l’esercitazione è il 741 che è alimentato con tensione continua di +12V
(+VCC) e -12V (-VCC).
Vi
R1
R3
+Vcc
VX
R2
2
[schema del circuito e pin di collegamento
dell’integrato 741]
7
OP-AMP
6
VU
3
4
-Vcc
Segnali
Vi
Vu
VMAX = +1V VMAX = +2V
VMIN = -1V
VMIN = 0V
VPP = 2V
VPP = 2V
 Progettazione
Per determinare il valore delle resistenze e del segnale in ingresso VX è stato applicato il principio
di sovrapposizione degli effetti. Quindi si supposto di far agire un segnale per volta, determinando
l’effetto di ogni segnale.
Applicazione del principio di sovrapposizione degli effetti:
Vu  VuI  VuII
VuI   A1 * Vi
Dalla teoria sul sommatore sappiamo che A1 
R3
R1
VuII   A2 * V X
A2 
e
R3
R2
R3
R
 10 e 3  1; a questo punto sono stati scelti dei valori delle
R1
R2
resistenze che risolvevano le uguaglianze: R3 = 22 KΩ , R2 = 22KΩ e R1 = 2,2 KΩ
A questo punto sapendo il valore della tensione VUII  1V si può ricavare il valore della VX:
Inoltre A1 = 10 e A2 = 1, quindi
VuII   A2 * V X
→
1V  1*VX
→
VX  1V
-7-
+1
+0,1
-0,1
V'u
Vi
t
[diagramma raffigurante la
tensione Vi e la tensione
VUI ]
-1
V''
u
+1
t
[diagramma raffigurante
la tensione VUII ]
u
+2
[diagramma raffigurante
la tensione di uscita del
sommatore Vu]
t
[Diagrammi teorici in correlazione]
-8-
 Sperimentazione
La verifica dei calcoli teorici è stata fatta con l’utilizzo di OP-AMP 741.
Inizialmente è stato verificato il segnale di ingresso Vi generato da un generatore di funzioni e
visualizzato su uno oscilloscopio:
Teorici
VPP  0,2V
Pratici
VPP  0,1V
div
VMAX  0,1V
VMAX  0,1V
div
VMIN  0,1V
VMIN  0,1V
div
T  1ms
T  0,2 ms
F
F  1K Hz
div
* 2div  0,2V
*1div  0,1V
* (1)div  0,1V
* 5,2div  1,04ms
1
1

 0,96 K Hz
T 1,04ms
[sopra: tabella dei valori di Vi.
destra:segnale sull’oscilloscopio]
In secondo luogo è stata applicata la sovrapposizione degli effetti facendo agire:
- per primo il segnale Vi, quindi il segnale VUI
Teorici
VPP  2V
Pratici
VPP
 0,5V
VMAX  1V
VMAX  0,5V
VMIN  1V
VMIN  0,5V
T  1ms
div
* 3,9div  1,95V
div
*1,9div  0,95V
* (2)div  1V
div
T  0,2 ms
* 5div  1ms
div
[sopra: tabella dei valori di VUI .
destra:immagine del segnale sull’oscilloscopio]
-9-
-
in secondo il segnale VX, quindi il segnale VUII
Teorici
II
U
V
 1V
Pratici
II
U
V
 0,5V
div
* 2  1V
[sopra: tabella dei valori di VUII .
destra:immagine del segnale sull’oscilloscopio]
Infine è stata verificata l’uscita del sommatore mettendo i diagrammi in correlazione di Vi e Vu
Teorici
Pratici
VPP  2V
VPP  0,5V
div
VMAX  2V
VMAX  0,5V
div
VMIN  0V
VMIN  0,5V
div
T  1ms
T  0,2 ms
div
* 4div  2V
* 4div  2V
* 0div  0V
* 5div  1ms
[sopra: tabella dei valori di VUI .
destra: immagine diagrammi in correlazione Vi , Vu]
- 10 -
 Simulazione
- 11 -
FASE 2:
VERIFICA DEL COMPARATORE TRIGGER DI SCHMITT INVERTENTE
Nell’esercitazione il comparatore trigger di Schmitt è stato realizzato con l’aggiunta della rete
resistiva a reazione positiva formata a da due resistenze, R1 e R2 che, in questo caso, hanno lo stesso
valore (R1=R2 =10KΩ). Il comparatore è invertente e, per verificarlo, il segnale di ingresso (Vi) è
un segnale sinusoidale con 14V da picco a picco e una frequenza di 1KHz
+Vcc
Vi
7
2
OP-AMP
VU
6
[schema del comparatore TS con pin di collegamento
dell’integrato 714]
3
4
R2
-Vcc
I
VRif
R1
 Progettazione
Per ricavare le due tensioni di riferimento è stata applicata la formula, precedentemente citata:
VRif 
R1
* VU
R1  R2
Come gia descritto la Vu sarà un segnale ad onda quadra con tensioni di massimo e di minimo
coincidenti con la tensione di saturazione del comparatore. Nel caso preso in esame le tensioni sono
di +10V (+VSat) e -10V (-VSat), queste corrispondono alla tensione di alimentazione a cui vengono
sottratti 2 V. (+VSat = +VCC – 2V.).
Quindi le tensioni di riferimento saranno:
VT   VSat
R1
10 K
 10V
 5V
R1  R2
10 K  10 K
VT   VSat
R1
10 K
 10V
 5V
R1  R2
10 K  10 K
- 12 -
Vi(V)
+7
VT+
+5
t
VT -
-5
-7
Vi(V)
+10
t
-10
[Diagrammi temporali in correlazione di Vi e Vu]
u
+10
-5
0
+5
Vi
[curva di trasferimento]
-10
- 13 -
 Sperimentazione
Nella sperimentazione pratica, prima si è verificato il segnale di ingresso Vi,:
Teorici
VPP  14V
VMAX  7V
VMIN  7V
T  1ms
F  1KHz
Pratici
VPP  2V
VPP  2V
div
div
* 7div  14V
* 3,5div  7V
VPP  2V
* (3,5)div  7V
div
T  0,2 ms
* 5,1div  1,02ms
div
F 1
 0,980KHz
1,02ms
[segnale Vi. Sopra; tabella dei valori
Sinistra: immagine del segnale]
Dopo è stata verificata l’uscita del comparatore Vu.
Teorici
VPP  20V
VMAX  10V
VMIN  10V
T  1ms
TH  0,5ms
TL  0,5ms
Pratici
VPP  5V
* 4,2div  21V
div
VMAX  5V
* 2,2div  11V
div
VMIN  5V
* (2)div  10V
div
T  0,2 ms
* 5,2div  1,04ms
div
TH  0,2 ms * 2,7div  0,54ms
div
TL  0,2 ms
* 2,5div  0,5ms
div
[segnale Vu. Sopra; tabella dei valori
Destra: immagine del segnale]
- 14 -
I segnali sono stati visualizzati su un oscilloscopio, grazie al quale è stato possibile anche
visualizzare la curva di trasferimento caratteristica, con ciclo di isteresi.
Per ricavare la caratteristica il segnale di ingresso (Vi) è stato posizionato sul canale 1
dell’oscilloscopio (CH1), mentre il segnale di uscita (Vu) sul canale 2 (CH2). Inoltre il CH1 è stato
fissato su 2V/div mentre il CH2 su 5V/div. Premendo il pulsante XY sull’oscilloscopio è possibile
vedere la curva, in questo modo il segnale collegato a CH1 rappresenta l’ascissa del grafico, mente
quello collegato a CH2 rappresenta l’ordinata.
[immagine della curva di trasferimento sull’oscilloscopio]
Dall’immagine della curva di trasferimento si nota in che momento avviene il passaggio, già
spiegato nell’introduzione, da livello alto a livello basso e viceversa. Ed è proprio grazie a questo
passaggio che si elimina il disturbo che si può presentare sul segnale in ingresso.
- 15 -
 Simulazione
- 16 -
FASE 3:
VERIFICA DEL CIRCUITO INTEGRATORE E DERIVATORE
Questa verifica è svolta in 2 parti distinte, in quanto ognuno di questi circuiti è stato studiato
singolarmente dato che oltre ad essere 2 dispositivi distinti sono anche state utilizzate diverse
componenti.
 INTEGRATORE
L’integratore è stato realizzato con un condensatore ( C ) da 3,3 nF, una resistenza ( R1 ) da 10KΩ,
inoltre è stata aggiunta, in parallelo al condensatore, un’altra resistenza ( R2 )da 100 KΩ, creando in
questo modo un filtro che evita che l’integratore vada in saturazione perché si può integrare una
corrente continua casuale. L’utilità del filtro è quella di far passare una corrente continua media
annullando l’effetto della parte alternata della corrente. In ingresso è stato mandato un segnale a
onda quadra con 10 V picco-picco ( VPP ) e frequenza ( F ) da 8 KHz, quindi periodo ( T ) da 125μs.
R1
C
[schema dell’integratore con pin di
collegamento dell’OP-AMP]
+Vcc
Vi
R2
2
7
OP-AMP
6
VU
3
4
-Vcc
 Progettazione
Per determinare il segnale in uscita dall’integratore bisogna tener presente il che l’integrale di una
costante è una retta che tende a + ∞ se la costante e positiva, tende a - ∞ se la costante è negativa,
pertanto, dato che il segnale in ingresso presenta due livelli di tensioni costanti, in un certo periodo
di tempo, l’uscita sarà un segnale triangolare.
Per determinare il valore da picco a picco dell’uscita ( VuPP ) si utilizza la formula ricavata
precedentemente:
1
Vu  
Vi  dt
RC 
Di questa si considera il tempo in cui il segnale Vi rimane costante, ovvero il tempo in cui si ha il
livello alto del segnale ( VMAX ). Dato che il segnale ha un D.C del 50% il tempo in cui rimane
costante è la metà del periodo ( T/2) che indicheremo con TH ( durata del livello alto). Di
conseguenza la formula sopra descritta diventerà:
Vi  TH
Vu PP  
RC
A questo punto si può ricavare il valore da picco a picco del segnale in uscita:
T 125s
TH  
 62,5s
2
2
5V  62,5 10 6 s
Vu PP  
 9,47V  10V
10 10 3   3,3 10 9 F
- 17 -
V
i (V)
+5
TH
T
t
TL
-5
Vu (V)
+5
t
-5
[diagrammi Vi e Vu in correlazione]
 Sperimentazione
Verifica del segnale Vi:
Teorici
VPP  10V
VMAX  5V
VMIN  5V
T  125s
TH  62,5s
TL  62,5s
DC 
T
125s
 100 
 100  50%
TH
62,5s
F  8KHz
Pratici
VPP  5V
* 2div  10V
div
VMAX  5V
*1div  5V
div
VMIN  5V
* (1)div  5V
div
T  20 s
* 6,4div  128s
div
TH  20 s
* 3,2div  6,4ms
div
TL  20 s
* 3,2div  6,4ms
div
- 18 -
[immagine sull’oscilloscopio del segnale Vi]
Verifica del segnale Vu:
Teorici
VPP  10V
VMAX  5V
VMIN  5V
T  125s
Pratici
VPP  5V
* 2div  10V
div
VMAX  5V
*1div  5V
div
VMIN  5V
* (1)div  5V
div
T  20 s
* 6,4div  128s
div
[immagine dell’oscilloscopio raffigurante i diagrammi di Vi e Vu in correlazione]
- 19 -
 Simulazione
Come precedentemente progettato il segnale in uscita è un segnale triangolare con valore da picco a
picco quasi uguale al segnale in ingresso.
- 20 -
 DERIVATORE
Il derivatore è stato realizzato con un condensatore ( C ) da 3,3nF, una resistenza ( R1 ) da 10 KΩ e
come nel caso dell’integratore un’altra resistenza ( R2 ) da 1 KΩ, questa volta però posizionata in
serie al condensatore, utilizzata anche in questo caso come filtro per evitare gli effetti del disturbo.
In ingresso è stato mandato un segnale triangolare con 10 V picco-picco ( VPP ) e frequenza ( F ) da
2 KHz quindi periodo ( T ) di 500μs
R1
Vi
R2
+Vcc
C
2
[schema del derivatore con pin di collegamento
dell’OP-AMP]
7
OP-AMP
6
VU
3
4
-Vcc
 Progettazione
La derivata rappresenta il coefficiente angolare di una retta tangente a una funzione.
Nel caso specifico per calcolare la derivata del segnale in ingresso (Vi) si utilizza una formula,
precedentemente descritta, del tipo :
dVi
Vu   RC
dt
dVi
coefficiente angolare della retta
dt
Quindi avremo :
Vi
dVi
 tg  PP
T
dt
2
A questo punto si possono calcolare le due correnti di picco del segnale in uscita ( Vu )
Vi
10V
Vu MIN   RC PP  10  10 3   3,3  10 9 F
 1,32V
T
500  10 6 s
2
2
Vi
10V
Vu MAX   RC PP  10  10 3   3,3  10 9 F
 1,32V
T
500  10 6 s
2
2
Vu PP  Vu MAX  Vu MIN  2,64V
- 21 -
i (V)
+5
T
2
T
t
-5
Vu (V)
+1,32
t
-1,32
[diagrammi Vi e Vu in correlazione]
 Sperimentazione
Verifica del segnale Vi:
Teorici
Pratici
VPP  10V
VPP  2V
div
VMAX  5V
VMAX  2V
div
VMIN  5V
VMIN  2V
T  500 s
T  0,2 ms
F  2 KHz
F 1
div
div
* 5div  10V
* 2,5div  5V
* (2,5)div  5V
* 2,7div  0,54ms
0,54ms
 1,85KHz
[immagine sull’oscilloscopio del segnale Vi]
- 22 -
Verifica del segnale Vi:
Teorici
Pratici
VPP  2,64V
VPP  0,5V
div
VMAX  1,32V
VMAX  0,5V
div
VMIN  1,32V
* 3,7div  1,85V
VMIN  0,5V
T  500s
TH  250s
TL  250s
DC 
* 7,4div  3,8V
T
500 s
 100 
 100  50%
TH
250 s
* (3,7)div  1,85V
div
T  0,2 ms * 2,7div  0,54ms
div
TH  0,2 ms
*1,4div  0,28ms
div
TL  0,2 ms *1,4div  0,28ms
div
F  2 KHz
[immagine sull’oscilloscopio del segnale Vi]
[immagine dell’oscilloscopio raffigurante i diagrammi di Vi e Vu in correlazione]
- 23 -
 Simulazione
- 24 -
CONCLUSIONI
Considerando le difficoltà trovate in alcuni casi, l’esercitazione è avvenuta con successo. Tutti i
valori ottenuti dalla progettazione delle fasi sono stati verificati dalle sperimentazioni pratiche e
dalle simulazioni ( effettuate tutte con softwere EWB ).
- 25 -