IL GRAFICO SPAZIO-TEMPO
Ormai dovreste aver già capito una cosa fondamentale: la Fisica studia soltanto proprietà che possono
essere espresse o con numeri o con grandezze geometriche come ad esempio i vettori. Finora
abbiamo trattato il movimento attraverso numeri: è giunta l’ora di descriverlo anche con la geometria.
Lo strumento con cui si geometrizza il movimento è il Grafico Spazio-Tempo (Grafico S-t), cioè quel
grafico che riporta sull'asse delle X il tempo (t) e sull'asse delle Y la posizione del corpo in
movimento (S).
Possiamo affermare che il Grafico S-t è l'espressione geometrica del movimento: in altre parole, ciò
che in Fisica appare come movimento in Geometria diventa il Grafico S-t. Posso dire di piu': qualsiasi proprietà
cinematica è esprimibile all'interno del Grafico S-t ; all'opposto, dal Grafico S-t è ottenibile ogni proprietà
cinematica del movimento. Vediamo adesso di mettere in pratica con qualche esempio quello che abbiamo
appena affermato.
Durante le Olimpiadi di Pechino, Usain Bolt stabilì il record del mondo dei 100 m col tempo di 9,69 s.
La tabella riporta i suoi tempi di passaggio ogni 10 m.
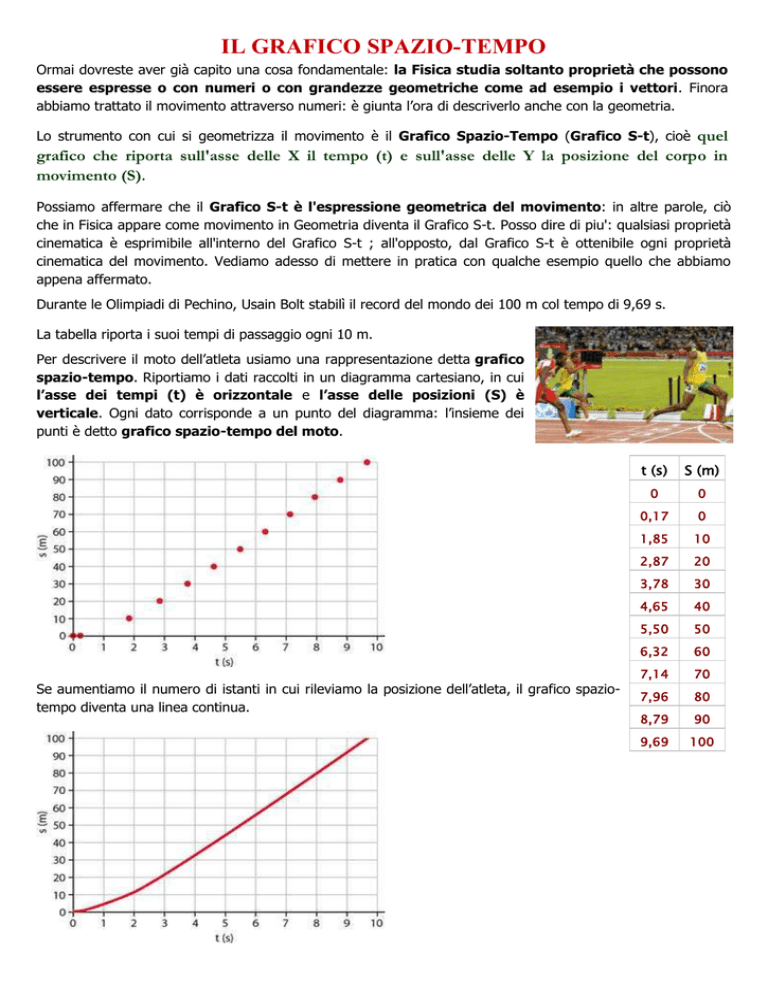
Per descrivere il moto dell’atleta usiamo una rappresentazione detta grafico
spazio-tempo. Riportiamo i dati raccolti in un diagramma cartesiano, in cui
l’asse dei tempi (t) è orizzontale e l’asse delle posizioni (S) è
verticale. Ogni dato corrisponde a un punto del diagramma: l’insieme dei
punti è detto grafico spazio-tempo del moto.
Se aumentiamo il numero di istanti in cui rileviamo la posizione dell’atleta, il grafico spaziotempo diventa una linea continua.
t (s)
S (m)
0
0
0,17
0
1,85
10
2,87
20
3,78
30
4,65
40
5,50
50
6,32
60
7,14
70
7,96
80
8,79
90
9,69
100
Pendenza e velocità media
Il grafico spazio-tempo contiene molte informazioni sul moto di un corpo. In particolare, permette di calcolare
la velocità media (e poi anche la velocità istantanea, come dimostreremo fra breve) con semplici
considerazioni geometriche.
Consideriamo per esempio il moto di Bolt tra gli istanti tA = 5,5s e tB = 8,0s , cioè nell’intervallo di tempo
Δt= tB − tA = 8,0s − 5,5s = 2,5s. Durante questo intervallo la posizione dell’atleta cambia da sA = 50m a sB =
80m, quindi lo spostamento è Δs = sB − sA = 80m − 50m =+30m. Il rapporto Δs/Δt
è
chiamato pendenza o coefficiente angolare della retta secante passante per A e B:
Pendenza della secante = Δs/Δt = +30m/2,5s = +12m/s
Come voi già sapete, il rapporto Δs/Δt è proprio la definizione di velocità media. Quindi:
la velocità media di un certo intervallo di tempo è uguale alla pendenza della secante che
congiunge i punti iniziale e finale del movimento nel grafico spazio-tempo
Nel caso di un corpo che si muove nel verso positivo del sistema di riferimento, la velocità è positiva. In
questo caso, minore è la pendenza del grafico spazio-tempo, minore è la sua velocità. La pendenza del grafico
spazio-tempo fra i punti O e C è minore di quella fra i punti A e B. Infatti, la velocità media nei primi 2,0 s di
gara è solo
Vm = Δs/Δt = [12m−0m]/[2,0s−0,0s] = 12m/2,0s = 6,0m/s
Il testo è una rielaborazione di materiale estratto dall’e-book “Fisica e realtà” di Romeni
Claudio, Zanichelli ed.












