Matematica Discreta I - Matematica e Informatica

Matematica Discreta
Lezione del giorno 18dicembre 2009
Colorazione di una mappa geografica e di un grafo
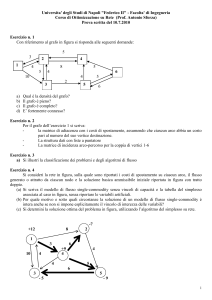
Nell’800 fu posto il seguente problema: qual è il minimo numero di colori necessario per colorare le
regioni di una qualunque mappa geografica, con la condizione che regioni confinanti abbiano colori
diversi ?
Tale problema fu risolto nel 1977 da Appel e Haken, con la dimostrazione del “teorema dei 4
colori”, il quale afferma che 4 colori bastano per qualunque mappa geografica.
Si può interpretare tale problema nel linguaggio della teoria dei grafi: infatti a una mappa
geografica si può associare un grafo in cui ogni vertice rappresenta una regione, e due vertici sono
collegati da un arco se le regioni corrispondenti sono confinanti.
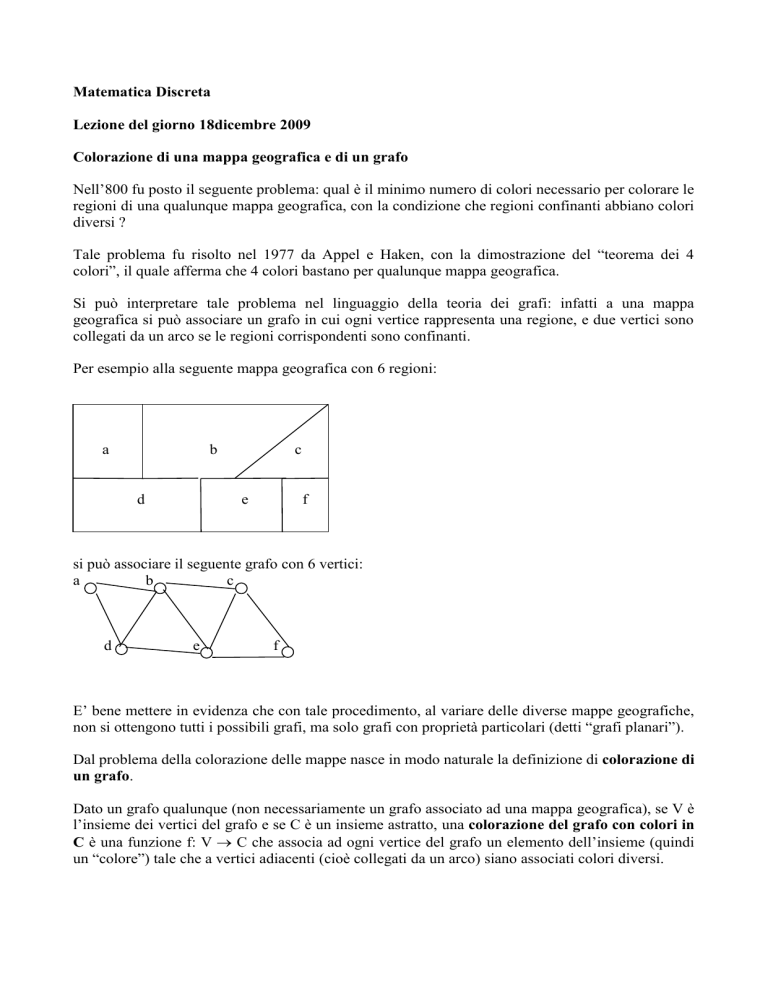
Per esempio alla seguente mappa geografica con 6 regioni:
a
b
d
c
e
f
si può associare il seguente grafo con 6 vertici:
a
b
c
d
e
f
E’ bene mettere in evidenza che con tale procedimento, al variare delle diverse mappe geografiche,
non si ottengono tutti i possibili grafi, ma solo grafi con proprietà particolari (detti “grafi planari”).
Dal problema della colorazione delle mappe nasce in modo naturale la definizione di colorazione di
un grafo.
Dato un grafo qualunque (non necessariamente un grafo associato ad una mappa geografica), se V è
l’insieme dei vertici del grafo e se C è un insieme astratto, una colorazione del grafo con colori in
C è una funzione f: V  C che associa ad ogni vertice del grafo un elemento dell’insieme (quindi
un “colore”) tale che a vertici adiacenti (cioè collegati da un arco) siano associati colori diversi.
Il numero cromatico di un grafo è il minimo numero di colori che servono per ottenere una
colorazione del grafo, quindi è la minima cardinalità di un insieme C tale che esista una colorazione
del grafo con colori in C.
Con questo linguaggio il “teorema dei 4 colori” afferma che: il numero cromatico del grafo
associato ad una qualunque carta geografica è  4.
Esempio: nel seguente grafo con 5 vertici
e
a
b
c
d
si può ottenere per esempio una colorazione con 5 colori (con C={1,2,3,4,5}) associando al vertice
a il colore 1, al vertice b il colore 2, al vertice c il colore 3, al vertice d il colore 4, al vertice e il
colore 5.
Ma si può ottenere anche una colorazione con 4 colori (con C={1,2,3,4}) associando al vertice a il
colore 1, al vertice b il colore 2, al vertice c il colore 3, al vertice d il colore 4, al vertice e il colore
2.
Possiamo ancora risparmiare sul numero di colori, ed ottenere una colorazione con 3 colori (con
C={1,2,3}) associando al vertice a il colore 1, al vertice b il colore 2, al vertice c il colore 3, al
vertice d il colore 1, al vertice e il colore 2.
D’altra parte è impossibile ottenere una colorazione con 2 colori perché i 3 vertici b,c,d (essendo a 2
a 2 adiacenti fra loro) necessitano di 3 colori differenti. Dunque si conclude che il numero
cromatico di questo grafo è 3.
Caratterizziamo i grafi con “basso” numero cromatico. E’ ovvio che un grafo ha numero cromatico
1 se e solo se ha solo vertici isolati (quindi se e solo se non vi sono archi nel grafo). Per il numero
cromatico 2 vi è il seguente risultato:
Teorema. Sia dato un grafo in cui non tutti i vertici sono isolati (quindi con numero cromatico >1) .
Allora:
il numero cromatico del grafo è 2  tutti i cammini ciclici nel grafo hanno lunghezza pari.
Per dimostrare tale teorema dobbiamo però introdurre il concetto di componente connessa in un
grafo.
Dato un grafo, definiamo componente connessa un grafo ottenuto considerando come vertici tutti
quelli del grafo che sono fra loro uniti da qualche cammino, e come archi tutti quelli del grafo che
uniscono tali vertici.
Esempio: dato il seguente grafo con 9 vertici a,b,c,d,e,f,g,h,i, e 7 archi 1,2,3,4,5,6,7:
1
a
2
b
c
3
d
4
g
e
5
6
h
f
7
i
esso ha 3 componenti connesse formate rispettivamente dai vertici {a,b} (e dall’arco 1), dai vertici
{c,d,g} (e dagli archi 2,4), dai vertici {e,f,h,i} (e dagli archi 3,5,6,7).
E’ ovvio che ognuna delle componenti connesse di un grafo, considerata come grafo a sé stante, è
un grafo connesso, anche se il grafo originario non è connesso: infatti per costruzione fra 2 vertici
qualunque della stessa componente connessa esiste sempre almeno un cammino.
E’ ovvio anche che un grafo connesso ha 1 sola componente connessa, coincidente con l’intero
grafo.
Infine notiamo che v,w sono vertici del grafo in componenti connesse diverse allora non esiste un
cammino che li unisce (altrimenti apparterrebbero alla stessa componente) e in particolare non
esiste un arco che ha v,w come estremi (un arco è un cammino di lunghezza 1) dunque v,w non
sono adiacenti.
Da questa ultima osservazione segue che per calcolare il numero cromatico di un grafo, possiamo
servirci delle sue componenti connesse nel modo seguente: nella colorazione dei vertici del grafo
possiamo colorare i vertici di ogni componente connessa, potendo riutilizzare gli stessi colori nelle
diverse componenti (perché vertici in componenti diverse non sono mai adiacenti). Da tale
ragionamento segue allora che il numero cromatico del grafo sarà il più grande dei numeri cromatici
delle singole componenti connesse (la componente connessa che “pretende” più colori ha la
prevalenza).
Nel grafo esaminato nell’esempio precedente:
1
2
a
b
c
d
4
g
3
e
5
h
6
f
7
i
si verifica facilmente che i numeri cromatici delle 4 componenti connesse sono rispettivamente 2, 2,
3, dunque il numero cromatico dell’intero grafo è 3.