LICEO SCIENTIFICO “CAVOUR”
Compito di Fisica per la classe 3F . Recupero Durata della prova 1 ora
1) Achille e la tartaruga gareggiano ai giorni nostri e la tartaruga parte col vantaggio di 2 metri
Il << piè-veloce>> corre alla velocità di 10 m/s, la tartaruga, che in effetti è una tartaruga elettronica ,
corre con la velocità di 6 m/s. Traccia il grafico delle due leggi orarie e determina dopo quanto tempo
avverrà l’incontro
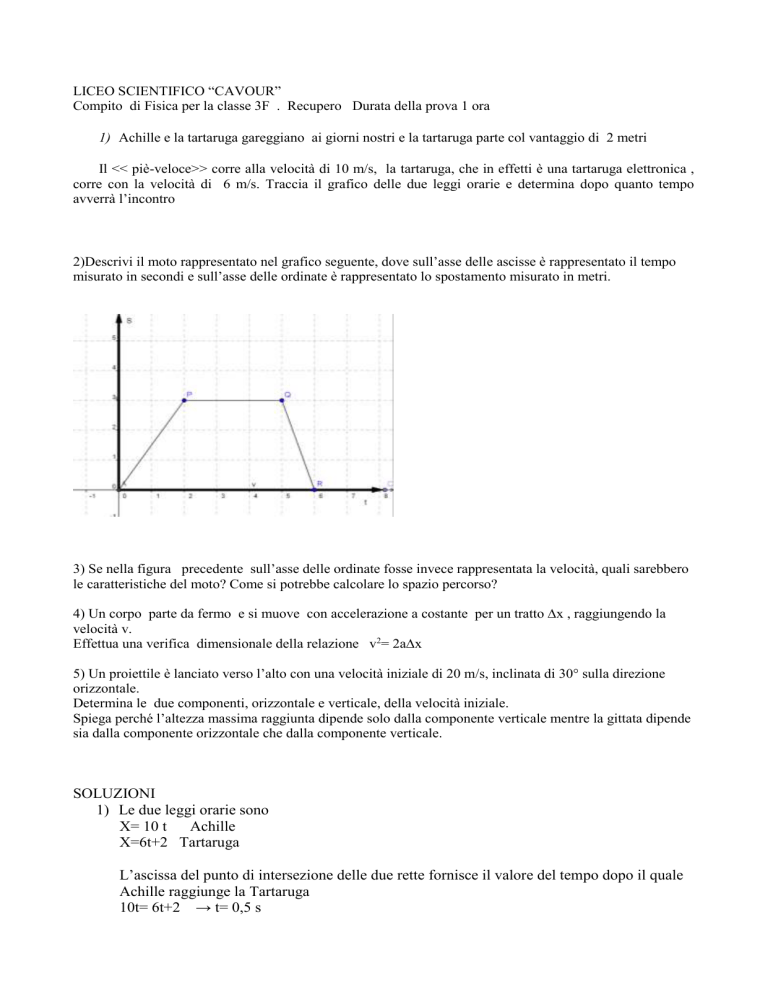
2)Descrivi il moto rappresentato nel grafico seguente, dove sull’asse delle ascisse è rappresentato il tempo
misurato in secondi e sull’asse delle ordinate è rappresentato lo spostamento misurato in metri.
3) Se nella figura precedente sull’asse delle ordinate fosse invece rappresentata la velocità, quali sarebbero
le caratteristiche del moto? Come si potrebbe calcolare lo spazio percorso?
4) Un corpo parte da fermo e si muove con accelerazione a costante per un tratto ∆x , raggiungendo la
velocità v.
Effettua una verifica dimensionale della relazione v2= 2a∆x
5) Un proiettile è lanciato verso l’alto con una velocità iniziale di 20 m/s, inclinata di 30° sulla direzione
orizzontale.
Determina le due componenti, orizzontale e verticale, della velocità iniziale.
Spiega perché l’altezza massima raggiunta dipende solo dalla componente verticale mentre la gittata dipende
sia dalla componente orizzontale che dalla componente verticale.
SOLUZIONI
1) Le due leggi orarie sono
X= 10 t
Achille
X=6t+2 Tartaruga
L’ascissa del punto di intersezione delle due rette fornisce il valore del tempo dopo il quale
Achille raggiunge la Tartaruga
10t= 6t+2 → t= 0,5 s
2) Il punto, partendo dall’origine del riferimento, si muove inizialmente , per 2s, di moto
uniforme con v= 1,5 m/s (tratto AP), poi si ferma per 3 secondi (tratto PQ) e riprende a
muoversi in verso contrario con velocità pari a -3 m/s ( il segno (-) indica che il punto si
avvicina all’origine), ritornando al punto di partenza (tratto QR)
3)Se i valori delle ordinate rappresentano la velocità ( supponiamo in m/s) possiamo dire invece
che:
Il moto è accelerato nei primi 2secondi ( a=1,5 m/s2), uniforme nel tratto PQ ( v=3 m/s) e
decelerato nel tratto QR ( a= -3 m/s2) .
Il punto parte da fermo e si fermerà di nuovo dopo 6 secondi.
Il modo più semplice per calcolare lo spazio percorso consiste nel calcolare l’area sottesa dal
grafico rappresenta la velocità , il trapezio APQR.
Spazio = Area = (6+3)3/2 = 13,5 m.
Allo stesso risultato ovviamente si perviene scrivendo la legge oraria del moto relativamente a
ciascun intervallo di tempo ( avendo l’accortezza di calcolare ∆x e non x)
∆x= ½ a t2 = 3m nei primi 2 secondi
∆x= vt = 9 m nei successivi 3 secondi
∆x=vo + t½ a t2 =( 3- 1,5) m = 1,5 m nell’’ultimo intervallo
∆S = (3+9+1,5) m = 13,5 m.
4)Verifica dimensionale v2= 2a∆x
( L lunghezza t tempo)
(L*t-1)2 = (L*t -2) *L
L2 t -2= L2 t -2
5) Vox = Vo cos 30° = 17,3 m/s circa Voy = V sen 30° = 10 m/s
Le equazioni parametriche del moto sono
I due moti, orizzontale e verticale, non si influenzano a vicenda, quindi l’altezza massima raggiunta
( Il proiettile si ferma in aria dopo t = Voy/ g secondi e raggiunge una quota h = ½ Voy 2/g
La gittata sarà x= Vox* Voy /g))
Dipende solo da Voy. Poiché da quest’ultima però dipende anche il tempo in cui il proiettile resta
in volo, la gittata dipende da entrambe le componenti












