Esercizi cinematica
1. In un grafico v-t un moto rettilineo uniforme è
rappresentato da:
A. una retta orizzontale
B. una retta qualsiasi
C. una parabola
D. una retta verticale
10. Achille corre a 10km/h, la Tartaruga a 0.5
km/h. La tartaruga parte con un vantaggio di
1000 m su Achille.
2. Un corpo cade partendo da fermo per 3 s. Qual
è la velocità finale?
A. 3 m/s
B. 29,4 m/s
C. 0,31 m/s
D. 3,27 m/s
i. Scrivi le leggi orarie del moto di Achille e
della Tartaruga e fai un grafico s-t dei due
moti.
ii. Dopo quanto tempo Achille supererà la tartaruga?
iii. Dove Achille supererà la tartaruga?
3. Un corpo inizialmente a velocità di 1 m/s accelera con accelerazione costante di 2 m/s2. Quanto
spazio percorre in 2 s
A. 6 m
B. 4 m
C. 2 m
D. 10 m
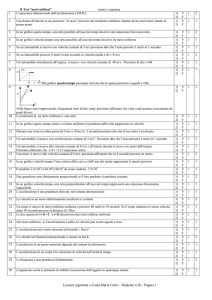
11. Il grafico velocità-tempo di un ciclista è riportato in figura. Calcolare lo spazio percorso dopo
2.0 s e dopo 4.0 s e la velocità media nei primi
4.0 s.
𝑣(𝑚/𝑠)
i. Dopo quanto tempo arriva al suolo.
ii. Con che velocità arriva al suolo.
12
10
4. Un macchina si muove a velocità costante di
10 m/s. In 10 minuti percorre un tragitto di:
A. 100 m
B. 6000 m
C. 1000 m
D. 600 m
2
4
𝑡(𝑠)
5. Il grafico v-t di un moto uniformemente accelerato è rappresentato da:
A. una retta
B. una retta orizzontale
C. una parabola
D. nessuna delle risposte precedenti
6. L’unità di misura dell’accelerazione nel SI è:
A. m/s
B. m/s2
C. m2 /s2
D. km/h
7. Se la velocità di un motociclista, in 10, 0 s, passa
da 32, 0 km/h a 59, 0 km/h, la sua accelerazione
media risulta:
A. 0, 750 m/s2
B. 2, 70 m/s2
C. 9, 72 m/s2
D. 972 m/s2
8. In un grafico v-t, una retta orizzontale rappresenta:
A. un corpo fermo
B. un corpo in moto uniformemente accelerato
C. un corpo in moto rettilineo uniforme
D. nessuna delle precedenti
9. Una tegola casca da un tetto alto 20 m.
Pagina 1 di 3
mag. 2016 (W19)
Soluzioni
Soluzione 1.
A
Soluzione 2.
B
Soluzione 3.
A
Soluzione 4.
B
Soluzione 5.
A . una retta
Soluzione 6.
B
Soluzione 7.
A
Soluzione 8.
C
Soluzione 9.
La tegola che casca dal tetto effettua un moto uniformemente accelerato con accelerazione
9,8 m/s2 e con velocità iniziale nulla. Il tempo per percorrere un tragitto ℎ è quindi
𝑡=√
2ℎ
= 2, 02 s
𝑔
La velocità con cui arriva al suolo si può quindi calcolare come:
𝑣 = 𝑔 ⋅ 𝑡 = 19, 8 s
Soluzione 10.
i. Legge oraria di Achille:
𝑠u� = 10 km/h ⋅ 𝑡
Legge oraria della Tartaruga:
𝑠(𝑘𝑚)
𝑠u� = 0.5 km/h ⋅ 𝑡 + 1 km
1
0.1
𝑡(ℎ)
Grafico:
ii. Uguagliando 𝑠u� e 𝑠u� e risolvendo l’equazione si ottiene l’istante in cui avviene il sorpasso:
𝑡=
1 km
= 0.105 h
10 km/h − 0.5 km/h
iii. Mettendo il tempo trovato in una delle due leggi orarie si trova la posizione del sorpasso:
𝑠 = 10 km/h ⋅ 0.105 s = 1.05 s
Soluzione 11.
Lo spazio percorso si trova come area sottesa dal grafico v-t. Lo spazio percorso dopo 2 s
è l’area di un rettangolo:
𝑠2u� = 10 m/s ⋅ 2 s = 20 m
Dopo quattro secondi a questo spazio bisogna aggiungere l’area di un trapezio rettangolo:
Pagina 2 di 3
mag. 2016 (W19)
𝑠4u� = 20 m +
(10 m/s + 12 m/s) ⋅ 2 s
= 20 m + 22 m = 44 m
2
La veocità media nei primi 4 s è:
𝑣u� =
Δ𝑠
44m
=
= 11m/s
Δ𝑡
4s
Pagina 3 di 3
mag. 2016 (W19)