esame 16 luglio 2012 - INFN-CS

MECCANICA E TERMODINAMICA
16 luglio 2012
(Per l’ esame di “Meccanica e Termodinamica” esercizi n. 1 - 2 – 3)
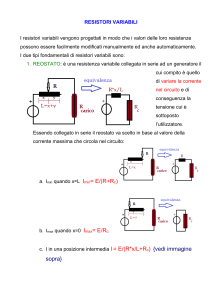
1.
Una molla, di costante elastica K = 200 N/m e lunghezza a riposo L = 1 m, è vincolata al
suolo per un estremo e disposta verticalmente. Un corpo di massa M = 2 kg cade (ossia è
nulla la velocità iniziale) sulla molla da un’altezza, calcolata dall’estremo libero, h=2 m.
A seguito dell’urto il corpo rimane attaccato alla molla che inizia ad oscillare mantenendo
l’assetto verticale. Si determini, ponendo lo zero dell’energia potenziale gravitazionale
alla quota del suolo, il valore numerico dell’energia potenziale del corpo alla quota
corrispondente alla massima compressione della molla.
(Sono trascurabili tutte le forze di attrito ed è trascurabile la massa della molla.
Si usi come valore dell’accelerazione di gravità g = 9.81 m/s2 )
2. Un oggetto, di dimensioni trascurabili e di massa M = 2 Kg, ruota con velocità angolare ω0 = 3 rad/s.
L’oggetto, poggiato su un piano orizzontale liscio, è connesso al centro della traiettoria tramite un filo di
lunghezza L=2 m. Al tempo t =0 viene applicata all’oggetto una forza di modulo costante, (F = 20 N), la
cui direzione e verso coincidono, in ogni istante, con la direzione e verso della velocità tangenziale.
Si determini dopo quanto tempo, dall’applicazione della forza F, la forza centripeta assumerà un valore
doppio rispetto a quello iniziale.
Si determini il lavoro fatto dalla forza centripeta nell’intervallo di tempo considerato.
3. Una massa M = 1000 g di aria è contenuta in un recipiente cilindrico chiuso da un pistone mobile di
diametro D = 60 cm. Si calcoli di quanto si sposterà il pistone se, mantenendo la pressione costante (P =
1,013 105 Pa) e fornendo all’aria una quantità di calore Q = 9960 J, la temperatura dell’aria aumenta di
10 K.
Si consideri l’aria un gas perfetto biatomico di peso molecolare 29.
Calori specifici molari:
ed R = 8.31 J/ mol K.
4.
Una macchina termica ipotetica opera con un ciclo costituito da due isobare e due
isocore. Il fluido operante è un gas perfetto monoatomico.
Sapendo che i volumi minimo e massimo sono rispettivamente Vmin = 25 m3 e
Vmax = 50 m3 e che le pressioni minima e massima sono rispettivamente
Pmin = 1.01 105 Pa e Pmax =2.02 105 Pa, si determini il rendimento della macchina.
Calori specifici molari: Cv = (3/2) R, Cp = (5/2) R ed R = 8.31 J/ mol K.
Soluzione 1
Applichiamo la conservazione dell’ energia eguagliando l’ energia iniziale (corpo fermo a quota L+h e molla a
riposo) all’ energia del sistema nello stato di massima compressione.
L’ energia iniziale e’ l’ energia potenziale della massa M
M g (h + L)
Nel punto di massima compressione della molla il sistema ha di nuovo solo energia potenziale, ed indicando con
D il tratto di cui si e’ compressa la molla avremo:
Mg (L-D) = energia potenziale del corpo
.5 K D 2 = energia potenziale della molla
2
Da cui:
M g (h + L) = Mg (L-D) + .5 K D  D = .73 m
energia potenziale del corpo = Mg (L-D) = 5.29 J
Soluzione 2.
La forza centripeta e’ inizialmente : Fc1 = M L ω02
Quando questa assume un valore doppio avremo Fc2=2 Fc1 = M L ω 2 . Da cui ω = ω0 √2 ;
ω = ω0 + α t
Dove ω e’ la velocita’ angolare acquistata per effetto della accelerazione angolare α = F/(M L), dovuta all’
applicazione della forza F.
t = (ω - ω0 )/ α = ω0(√2 -1) L M /F = .25 s
La forza centripeta e’ perpendicolare allo spostamento e non fa’ quindi lavoro.
Soluzione 3.
Dal I principio della termodinamica ∆U = Q –L possiamo calcolare il lavoro
L = Q - ∆U
Poiché per un gas perfetto la variazione di energia interna e’ data da : ∆U = n Cv ∆T
Risulta ∆U = (1000/29) x (5/2) x 8.31 x 10 = 7163.8 J
L = 9960 – 7163.8 = 2796.2 J
Essendo la trasformazione a pressione costante: L = P∆V dove ∆V = S ∆H (con S sezione del recipiente ed ∆H
spostamento del pistone.
∆H = L /( P S) = 2796.2/ (1,013 10 5 x 3.1415 x .32 ) = 9.76 cm
Soluzione 4.
Con riferimento alla figura abbiamo:
in A
Pa = Pmax;
Va = Vmin;
Ta = Pmax Vmin /n R
in B
Pb = Pmax;
Vb = Vmax;
Tb = Pmax Vmax /n R
in C
Pc = Pmin;
Vc = Vmax;
Tc = Pmin Vmax /n R
in D
Pd = Pmin;
Vd = Vmin;
Td = Pmin Vmin /n R
Il rendimento e’ dato dal rapporto tra il lavoro L nel ciclo ed il calore Q assorbito: η = L/Q
AB:
BC:
CD:
DA:
Lab = Pmax (Vmax - Vmin)
Lbc = 0
Lcd = - Pmin (Vmax - Vmin)
Lda = 0
Qab = nCp (Tb-Ta) = (5/2) Pmax (Vmax - Vmin)
Qbc = nCv(Tc-Tb) = - (3/2) Vmax (Pmax - Pmin)
Qcd = nCp (Td-Tc) = - (5/2) Pmin (Vmax - Vmin)
Qda = nCv (Ta-Td) = (3/2) Vmin (Pmax - Pmin)
[>0]
[<0]
[<0]
[>0]
Ltot = (Pmax-Pmin) (Vmax – Vmin)
Qass = (5/2)Pmax (Vmax- Vmin) +(3/2) Vmin (Pmax-Pmin)
η = 2 (∆P ∆V) / ( 3 ∆P Vmin + 5 ∆V Pmax) = 0.1538