TEMI D’ESAME 2003-2004
Aprile 2004:
Ingegneria Edile - Fisica sperimetale A+B
I Prova in Itinere 26/04/2004
Problema 1
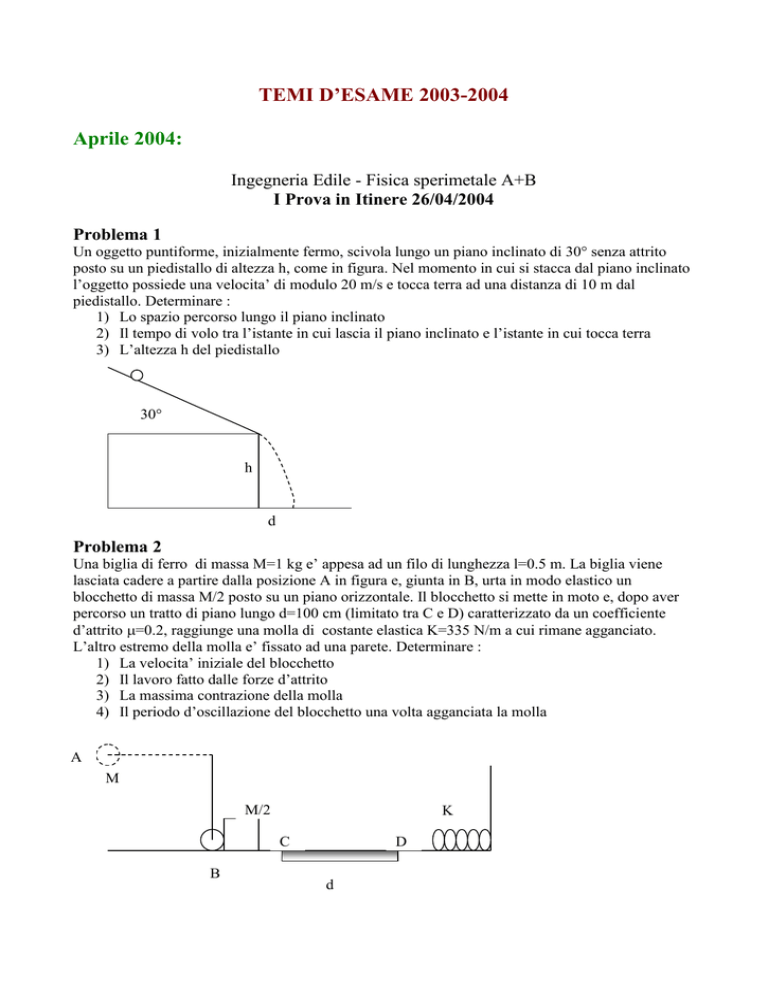
Un oggetto puntiforme, inizialmente fermo, scivola lungo un piano inclinato di 30° senza attrito
posto su un piedistallo di altezza h, come in figura. Nel momento in cui si stacca dal piano inclinato
l’oggetto possiede una velocita’ di modulo 20 m/s e tocca terra ad una distanza di 10 m dal
piedistallo. Determinare :
1) Lo spazio percorso lungo il piano inclinato
2) Il tempo di volo tra l’istante in cui lascia il piano inclinato e l’istante in cui tocca terra
3) L’altezza h del piedistallo
30°
h
d
Problema 2
Una biglia di ferro di massa M=1 kg e’ appesa ad un filo di lunghezza l=0.5 m. La biglia viene
lasciata cadere a partire dalla posizione A in figura e, giunta in B, urta in modo elastico un
blocchetto di massa M/2 posto su un piano orizzontale. Il blocchetto si mette in moto e, dopo aver
percorso un tratto di piano lungo d=100 cm (limitato tra C e D) caratterizzato da un coefficiente
d’attrito =0.2, raggiunge una molla di costante elastica K=335 N/m a cui rimane agganciato.
L’altro estremo della molla e’ fissato ad una parete. Determinare :
1) La velocita’ iniziale del blocchetto
2) Il lavoro fatto dalle forze d’attrito
3) La massima contrazione della molla
4) Il periodo d’oscillazione del blocchetto una volta agganciata la molla
A
M
M/2
K
C
B
D
d
Domanda
Si dia la definizione di forza conservativa, illustrandone le proprietà. Si indichi la relazione tra
lavoro di una forza conservativa e l’energia potenziale. Si dimostri in modo esplicito che la forza
A
gravitazionale e’ conservativa.
Ingegneria Edile - Fisica sperimetale A+B
I Prova in Itinere 26/04/2004
Soluzione Problema 1
1) l = h / sen = v2 / g
2) t = d / (v cos)
3) h = v sen t + 1/2 g t2
l = 40.8 m
t = 0.58 s
h = 7.45 m
Soluzione Problema 2
1) (v1)2 = 2 g l
v1 = v’1 + 1/2 v’2
(v1)2 = (v’1) 2 + 1/2( v’2) 2
2) L = - (g M/2) d
3) E’K = EK + L
E’K = + 1/2 K xmax 2
4) T = 2 (M/2K)
v’2 = 4.17 m/s
L = - 0.98 joule
xmax = 14 cm
T = 0.24 s
A
Giugno 2004:
Ingegneria Edile - Fisica sperimetale A+B
II Prova in Itinere 28/06/2004
Problema 1
Si consideri il circuito in figura :
R1 = 10
+
1 =10V
+
C
R2 = 20
2 =20V
Il condensatore piano C ha superficie S=0.2 cm2, distanza tra le armature d=0.1 cm ed e’ riempito
con un isolante avente costante dielettrica relativa k=2. Si determini :
1) La capacità del condensatore
2) La carica presente sulle armature a interruttore aperto (in condizioni stazionarie)
3) La carica presente sulle armature a interruttore chiuso (in condizioni stazionarie)
4) L’intensita’ e il verso della corrente attraverso R1 a interruttore chiuso (in condizioni
stazionarie)
(La costante dielettrica del vuoto e’ 0 = 8.85 x 10-12 C2/Nm2 )
Problema 2
Tre cariche elettriche sono disposte ai vertici di un triangolo equilatero di lato l = 10cm come in
figura :
Q1 = +q
Q2 = -2q
Q3 = +q
Si calcoli (assumendo q= e = 1.6 10-19 C) :
1) L’energia (potenziale) immagazzinata nel sistema
2) La forza agente sulla particella Q2
3) Il lavoro necessario per una forza esterna per portare Q2 a distanza infinita dalle altre cariche
Domanda
1) Si descriva la forza esercitata su una particella carica in moto in un campo magnetico (Forza
di Lorents)
2) Si indichi intensità, direzione e verso della forza agente sulla particella di carica negativa
(q= -e = -1.6 10-19 C) nella posizione in figura (B e v sono vettori nel piano del foglio):
|B| = 1T
45°
|v| = 1m/s
3) Quale sara’ la traiettoria seguita dalla particella?
4) Dopo aver percorso un metro, qual e’ il lavoro compiuto dal campo B sulla particella?
LUGLIO 2004
Ingegneria Edile - Fisica sperimetale A+B
Recupero 12/07/2004
Fisica A
Problema 1
La molla in figura (costante elastica k=100 N/m), avente un piatto di massa m=0.2 kg, viene
compressa di un tratto L1 (rispetto alla posizione di riposo X0) e successivamente viene lasciata
libera. Il piatto urta quindi (in modo istantaneo ed elastico) un cubo di eguale massa m posto a
distanza L2 =5cm da X0 che sale lungo il trampolino (inclinato di 30 gradi e lungo L3 =4cm) e
ricade a terra. Trascurando gli attriti e sapendo che quando passa per X0 prima dell’urto il piatto ha
una velocita’ di 3 m/s, si determini:
1) La lunghezza del tratto L1
2) La velocita’ del cubo subito dopo l’urto col piatto
3) La velocita’ con cui il cubo lascia il trampolino
4) La massima quota raggiunta dal cubo
L1
L2
L3
X0
Domanda 2
1) Si scriva l’equazione del moto di un corpo di massa m attaccato ad una molla orizzontale
con costante elastica k
2) Si scriva la soluzione generica di tale equazione e si indichi la frequenza delle oscillazioni
3) Si determini ampiezza e fase delle oscillazioni nel caso particolare in cui il corpo al tempo
t=0 si trovi nella posizione di riposo xo della molla con velocita’ v0
Ingegneria Edile - Fisica sperimetale A+B
Recupero 21/07/2004
Fisica A
Problema 1
Un pendolo conico e’ formato da un peso di massa m= 0.5 kg attaccato ad una fune inestensibile di
massa trascurabile e lunghezza s = 1m. Il pendolo, ruotando attorno ad un asse verticale, forma un
cono di semiapertura =30°, la cui base si trova ad un’altezza d di 50 cm da terra. Si determini :
1) La tensione della fune
2) La velocita’ angolare di rotazione
3) L’istante a cui il corpo toccherebbe il suolo se la corda si rompesse al tempo t=0.
d
Domanda 2
Si consideri un corpo puntiforme di massa m avente velocita’ (vettoriale) v e posizione istantanea
individuata dal vettore r, in un sistema inerziale di assi cartesiani aventi origine in O (punto fisso).
Sia F la forza agente sul corpo. Si definisca :
1) Il momento angolare L del corpo rispetto :
a. all’origine O degli assi cartesiani
b. ad un polo individuato dal vettore q
2) Il momento della forza rispetto ad O
3) Si enunci e si dimostri il teorema del momento angolare nel caso particolare in cui il polo
coincida con O
Ingegneria Edile - Fisica sperimetale A+B
Recupero 21/07/2004
TEMA A
Fisica A
Problema 1
1) Dall’equilibrio verticale : mg = Tcos, da cui T = mg/cos = 5.66N
T sin
2) Dall’equilibrio orizzontale : Tsen = m2R, da cui
mR
=3.36 rad/sec
R=s sin = 0.5 m
2d
3) d=1/2gt2 , da cui t
= 0.32 sec
g
g
tan
R
g
s cos
Domanda 2
1) a: Lo = r x mv, b: Lo’ = (r-q) x mv
2) Mo = r x F
3) d Lo/dt = dr/dt x mv + r x mdv/dt = v x mv + r x ma = r x F = Mo (il polo O e’ fisso !)
SETTEMBRE 2004
Ingegneria Edile - Fisica sperimetale A+B
Appello del 21/09/2004
Problema 1
Si consideri il sistema in figura. Il piano, perfettamente liscio, e’ inclinato di 45°. La molla ha
costante elastica k=50 N/m. Le masse valgono m1= 1 kg e m2= 2 kg. La fune e’ inestensibile ed ha
peso trascurabile. Determinare :
1) la tensione della fune all’equilibrio
2) l’energia (potenziale) elastica immagazzinata nella molla all’equilibrio
3) l’accelerazione dei due blocchi nel caso in cui m1 si staccasse dalla molla
m1
R2
m2
R1
Problema 2
Un condensatore sferico ha armature di raggio R1 = 10 cm e R2 = 20 cm ed e’ caricato con carica Q=
10-8 C. Un protone (m=1.7 10-27 kg, q=1.6 10-19 C) ruota uniformemente su un orbita circolare di
raggio R=15 cm tra le armature e concentrica col condensatore. Si calcoli :
1) La capacita’ del condensatore
2) Il valore del campo elettrico sull’orbita del protone
3) Il momento angolare del protone rispetto al centro dell’orbita
(0 = 8.85 10-12 C2/Nm2)
Domanda
1) Si enunci la legge di Ampère per campi magnetici generati nel
vuoto da correnti elettriche
i1
2) Si usi la legge di Ampère per dimostrare la legge di BiotSavart che descrive il campo magnetico generato da un filo
rettilineo indefinito percorso da corrente.
3) Si indichi intensità, direzione e verso della forza per unita’ di
lunghezza presente tra due fili rettilinei paralleli distanti d e
percorsi dalle correnti (equiverse) i1 e i2 come in figura.
Ingegneria Edile - Fisica sperimetale A+B
Appello del 21/09/2004
Soluzione A
Problema 1
T = m2 g
T = m1g /2 + kx da cui si ricavano T e x :
1) T = 19.6 N
2) E = ½ kx2 = 1.6 J
3) a = g(m2 - m1g /2 )/(m1+ m2) = 4.25 m/s2
i2
Problema 2
1) C = 40 R1R2/( R2 - R1) = 22 pF
2) E = Q/(40 R2) = 0.4 104 V/m
3) Eq = mv2/R da cui |L| = Rmv = 0.059 10-21 Nms
Soluzione B
Problema 1
T = m1 g
T + kx = m2g /2 da cui si ricavano T e x :
4) T = 9.8 N
5) E = ½ kx2 = 1.2 J
6) a = g(m2 - m1g /2 )/(m1+ m2) = 2.75 m/s2
Problema 2
4) C/l = 20 / ln(R2 / R1) = 80 pF
5) E = /(20 R) = 0.12 104 V/m
6) Eq = mv2/R da cui |L| = Rmv = 0.033 10-21 Nms












