Matematica

IClasse Seconda Liceo Scientifico Tecnologico
MODULO 0: RIPASSO E RACCORDO
PREREQUISITI
Calcolo numerico e letterale (I anno di corso)
OBIETTIVI
Ripassare insieme alcuni nodi fondamentali del calcolo letterale affrontati durante la prima
ed essenziali per impostare i nuovi contenuti di algebra di quest’anno
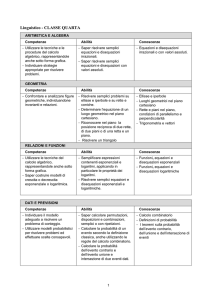
Unità 1: Equazioni lineari: Equazioni lineari numeriche intere e frazionarie. Problemi lineari.
Unità 2: Disequazioni lineari: Disequazioni lineari in una incognita intere. Sistemi di disequazioni
lineari. Disequazioni frazionarie. Disequazioni di grado superiore al primo fattorizzabili.
MODULO 1: SISTEMI LINEARI
PREREQUISITI
- conoscere e saper applicare le regole fondamentali del calcolo algebrico
- conoscere e saper applicare i principi di equivalenza delle equazioni
- saper risolvere equazioni di primo grado
- conoscere le proprietà dell’insieme dei numeri reali e saper operare in esso
- possedere il concetto di funzione
- saper riconoscere l’equazione di una retta
- saper rappresentare graficamente una retta dati i suoi parametri
OBIETTIVI
- saper codificare un problema lineare in due o più incognite con un modello algebrico
- saper risolvere un problema mediante la risoluzione di un sistema lineare in una o più
incognite
- saper verificare la correttezza dei risultati ottenuti sia algebricamente che graficamente
- saper determinare le posizioni relative di due rette nel piano cartesiano
- saper determinare le coordinate del punto di intersezione di due rette
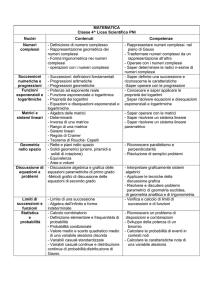
Unità 1: Sistemi numerici interi: Concetto di sistema. Grado di un sistema. Principi di
equivalenza. Risoluzione di un sistema numerico lineare con il metodo di sostituzione, di
confronto, di riduzione, di Cramer. Sistemi determinati, indeterminati , impossibili.
Sistemi numerici di tre equazioni in altrettante incognite. Modello matematico di un
problema aritmetico, geometrico o di altro genere in due o più incognite.
Unità 2: Risoluzione grafica di sistemi: Posizioni reciproche di due rette nel piano cartesiano.
Condizioni di incidenza, parallelismo e coincidenza di due rette rispetto ai coefficienti del
sistema. Risoluzione grafica di un’equazione e di un sistema lineare.
Unità 3: Sistemi letterali e fratti (Cenni): Risoluzione di sistemi lineari numerici fratti, letterali
interi, letterali fratti. Discussione delle soluzioni.
MODULO 2: NUMERI REALI
PREREQUISITI
- conoscere gli insiemi numerici N, Z e Q e saper operare in essi
- possedere il concetto di funzione e di corrispondenza biunivoca
OBIETTIVI
- saper definire e riconoscere un numero reale
- saper fissare un sistema di riferimento cartesiano su una retta
- saper operare con i radicali
- conoscere e saper operare con le potenze razionali di numeri reali
- saper risolvere equazioni e sistemi a coefficienti reali.
Unità 1: Insieme R: Ampliamento dell’insieme dei numeri razionali nell’insieme dei numeri reali.
Unità 2: Radicali: Concetto di radice aritmetica. Radici aritmetiche n-esime e relative proprietà e
operazioni. Concetto di radice algebrica. Razionalizzazione del denominatore di una
frazione. Potenze con esponente razionale e relative operazioni. Calcolo con i radicali.
Unità 3: Calcolo algebrico: Risoluzione di equazioni lineari, sistemi lineari e disequazioni lineari
con coefficienti irrazionali.
MODULO 3: EQUAZIONI E DISEQUAZIONI DI 2° GRADO
PREREQUISITI
- conoscere il calcolo algebrico
- possedere il concetto di equazione
- conoscere e saper applicare i principi di equivalenza delle equazioni
- saper operare con i radicali
- saper operare nel piano cartesiano
- saper rappresentare una retta nel piano cartesiano
- saper risolvere equazioni e disequazioni lineari.
OBIETTIVI
- saper riconoscere l’equazione di una parabola e saperla rappresentare nel piano
cartesiano
- saper risolvere algebricamente e graficamente equazioni e disequazioni di secondo grado
- riconoscere le posizioni relative di una retta e una parabola nel piano cartesiano
- saper risolvere algebricamente e graficamente un sistema di secondo grado
Unità 1: Equazioni di 2° grado: Risoluzione dell’equazione di secondo grado completa e
incompleta. Relazioni tra i coefficienti e le radici. Scomposizione in fattori di un trinomio
di secondo grado.
Unità 2: Funzione di 2° grado: Rappresentazione grafica di una funzione di secondo grado.
Determinazione del suo massimo o minimo. Zeri di una funzione di secondo grado.
Unità 3: Disequazioni di 2° grado: Risoluzione grafica delle disequazioni di secondo grado in una
variabile intere. Disequazioni frazionarie. Sistemi di disequazioni.
MODULO 4: EQUAZIONI E SISTEMI DI GRADO SUPERIORE AL 2°
PREREQUISITI
- saper risolvere equazioni e sistemi di primo e secondo grado
- conoscere il calcolo algebrico
- conoscere e saper applicare i principi di equivalenza delle equazioni
- saper operare con i radicali
OBIETTIVI
- saper riconoscere e risolvere equazioni e sistemi particolari di grado superiore al secondo
- saper riconoscere e risolvere equazioni irrazionali
- saper riconoscere la molteplicità di una soluzione
Unità 1: Equazioni di grado superiore al secondo: Equazioni abbassabili di grado. Equazioni
biquadratiche , binomie, trinomie.
Unità 2: Equazioni irrazionali: Definizione di equazione irrazionale. Equazioni irrazionali con un
solo radicale risolte mediante verifica delle soluzioni. Cenni a equazioni irrazionali con
due radicali.
Unità 3: Sistemi di grado superiore al primo: Sistemi di secondo grado. Sistemi simmetrici.
Sistemi di grado superiore al secondo risolvibili con il metodo di sostituzione.
MODULO 5: GEOMETRIA
Nota: lo scorso anno, a causa della riduzione delle ore settimanali di matematica (3 anziché 5), non
è stato possibile svolgere il modulo di geometria. Pertanto, in questo anno scolastico, la
realizzazione del modulo (eventualmente anche solo parziale) sarà a discrezione dell’insegnante, in
base all’opportunità rispetto alle esigenze specifiche della classe.
PREREQUISITI
Nessuno
OBIETTIVI
- concepire la geometria come uno dei possibili modelli della realtà
- comprendere l’impianto assiomatico-deduttivo della geometria euclidea
- conoscere le proprietà fondamentali delle figure piane notevoli
- saper impostare una dimostrazione secondo le regole della logica
- saper riconoscere figure congruenti, equivalenti, simili.
Unità 1: Il linguaggio della geometria: Enti geometrici fondamentali. Rette perpendicolari e
parallele. Criteri di parallelismo.
Unità 2: Figure piane notevoli: Triangoli e criteri di congruenza. Quadrilateri: trapezi e
parallelogrammi
Unità 3: Circonferenza e cerchio: arco, corda, angoli al centro ed alla circonferenza, proprietà
della circonferenza, posizioni reciproche retta/circonferenza, poligoni inscritti e circoscritti
Unità 4: Equivalenza delle superfici piane: figure equiscomponibili, primo e secondo teorema di
Euclide, teorema di Pitagora, applicazioni ai triangoli con angoli di 30°, 45°, 60°,
problemi di applicazione dell’algebra alla geometria
Unità 5: Triangoli simili: proporzioni tra grandezze, teorema di Talete, criteri di similitudine tra
triangoli, problemi di applicazione dell’algebra alla geometria
OBIETTIVI MINIMI
- Saper risolvere semplici sistemi lineari
- Saper risolvere semplici equazioni e disequazioni di secondo grado
- Saper rappresentare il grafico di una parabola
- Saper risolvere semplici equazioni di grado superiore al secondo