Primi elementi di geometria piana

WWW.MATEMATICAMENTE.IT
1
Primi elementi di geometria piana
Nome: _______________________________________ classe: _________ data: ____________
1. I termini primitivi sono elementi
che è necessario definire
che non si definiscono
che non si dimostrano
la cui definizione è data come nota
2. Un assioma è
un termine che non si definisce
una proposizione che non si dimostra
una proposizione che si dà per nota
una verità di tipo sperimentale
3. Un angolo è
la parte di
la parte di
la parte di
la parte di
piano
piano
piano
piano
delimitata
delimitata
delimitata
delimitata
da
da
da
da
due rette
due semirette
due semirette aventi l'origine in comune
due rette aventi un punto in comune
4. Quali affermazioni sono vere?
Per due punti passa sempre una sola retta
Per tre punti passa sempre una sola retta
Per due punti passa sempre un solo piano
Per tre punti passa sempre un solo piano
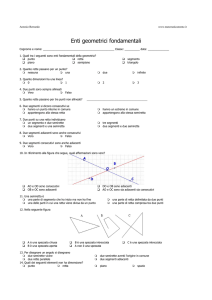
5. Relativamente alla figura
AB
BC
AC
AB
e
e
e
e
BC sono segmenti adiacenti
CD sono segmenti concavi
CE sono segmenti consecutivi
DE sono segmenti adiacenti
6. Quanti punti distinti occorre disegnare su una retta per avere due segmenti adiacenti?
1
2
3
4
7. Se AB e BC sono due segmenti adiacenti, la distanza tra M punto medio di AB e N punto medio di BC è
pari alla metà di AC
al doppio di BC
a un terzo di AC
alla metà della somma di AC e BC
WWW.MATEMATICAMENTE.IT
2
8. La poligonale in figura è
aperta intrecciata
chiusa intrecciata
aperta non intrecciata
chiusa non intrecciata
9. I due angoli rappresentati in figura sono
opposti al vertice
adiacenti
consecutivi
nessuna delle altre risposte
10. Due angoli la cui somma dà un angolo retto si dicono
complementari supplementari
ottusi
esplementari
11. Due angoli si dicono opposti al vertice se
hanno il vertice in comune
i lati di un angolo sono il prolungamento dei lati dell'altro
la loro somma dà 180°
la loro somma dà 360°
12. Quali delle seguenti affermazioni sono vere
Il doppio di un angolo acuto è sempre un angolo ottuso
Un angolo acuto è sempre convesso
Un angolo ottuso è sempre concavo
Se a e b sono angoli supplementari di c allora a e b sono congruenti
13. Un angolo a è i 4/5 del suo adiacente b. Quanto misurano a e b?
a=80°, b=100°
a=40°, b=50°
a=18°, b= 72°
a=30°, b=150°
14. I segmenti AB e CD sono disposti in modo da avere in comune il segmento CB congruente alla metà di AB.
Se ne può dedurre che
C è punto medio di AD
C è punto medio di AB
AB e CD sono adiacenti
I due segmenti giacciono sulla stessa retta
15. Due angoli a e b sono complementari, l'angolo formato dalle loro bisettrici misura
90°
45°
30°
non si può calcolare
WWW.MATEMATICAMENTE.IT
16. Le bisettrici di due angoli adiacenti sono
parallele
perpendicolari
3
coincidenti
opposte
17. Dati tre punti non allineati quante sono tutte le possibili rette distinte che li congiungono a due due?
2
3
4
5
18. M e N sono i punti medi dei due segmenti adiacenti AB e BC. Se BC=2AB allora
MN è la metà di BC
MN è il doppio di AB
MN è 2/3 di AB
MN è 3/2 di AB
WWW.MATEMATICAMENTE.IT
Soluzioni
1. B
2. B
3. C
4. AD
5. AC
6. C
7. A
8. A
9. D
10. A
11. B
12. BD
13. A
14. BD
15. B
16. B
17. B
18. D
4