La fisica quantistica
- Il corpo nero
La fisica classica (1900)
Leggi del mondo macroscopico:
• Equazioni di Newton del 1686 (fenomeni meccanici, acustici e termici)
• Equazioni di Maxwell del 1864 (fenomeni elettrici, magnetici e ottici)
La distinzione fra la natura ondulatoria della radiazione elettromagnetica
(diffrazione e interferenza) e la natura corpuscolare della materia era netta e
indiscutibile.
I problemi che misero in luce i limiti di validità delle leggi classiche furono il
corpo nero e quello della struttura dell’atomo.
Il corpo nero (1900)
Un corpo solido freddo non produce alcuna emissione, ma al crescere della
temperatura T comincia a diventare luminoso e a cambiare colore
emettendo, quindi, della radiazione.
• Esempio: un metallo che diventa incandescente cambia il suo colore e
diventa prima rosso, poi arancione, e infine giallo-bianco abbagliante
In prima approssimazione i corpi riscaldati seguono le stesse leggi di
emissione della radiazione tipiche di un corpo nero
Un corpo nero è un oggetto solido ideale in grado di assorbire
completamente (e poi riemettere) qualsiasi radiazione elettromagnetica
che incida sulla sua superfice
In pratica, però, nessun materiale assorbe tutta la radiazione incidente,
(la grafite ne assorbe il 97%)
Il corpo nero (1900)
Un corpo nero riscaldato ad una temperatura sufficientemente elevata
emette radiazioni
L’ energia emessa dipende solo dalla temperatura del corpo e non dalla
sua forma o dal materiale di cui è costituito
L’energia emessa da un corpo nero riscaldato ad una certa temperatura T
viene chiamata: radiazione di corpo nero
Un esempio pratico di corpo nero
Kirchhoff costruì il primo modello di corpo nero: un forno le cui pareti si
trovano a T costante e con un foro le cui dimensioni sono trascurabili
rispetto a quelle del corpo stesso
Un esempio pratico di corpo nero
L’energia entra da un piccolo foro e viene
assorbita dalle pareti del forno che si
riscaldano ed emettono radiazione
Le leggi sperimentali del corpo nero
Le relazioni cui obbedisce un corpo nero sono principalmente due:
• quella di Stefan-Boltzmann
• quella dello spostamento di Wien
Legge di Stefan-Boltzman
I = es T 4
All’aumentare della temperatura aumenta l’energia totale
La costante σ è detta costante di Stefan-Boltzmann e vale
5, 670 ×10-8 js-1m-2 K -4
Legge dello spostamento di Wien
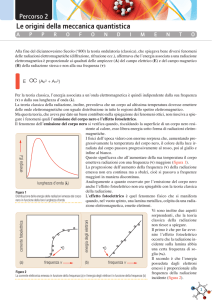
Lo spettro di emissione del corpo nero mostra un massimo di energia ad una
certa lunghezza d’onda (λmax)
All’aumentare della temperatura del corpo, la lunghezza d’onda del massimo
di emissione decresce
lT = k
k = 2,898×10 3 m × K
Spiegazione Wien
Wien trattò la radiazione all’interno di una cavità in modo analogo a un gas di
molecole e riuscì a dedurre una formula che riproduceva l’andamento generale
della curva di corpo nero, inclusa la presenza di un massimo di emissione, ma la
sua teoria falliva nel riprodurre i dati sperimentali alle grandi lunghezze d’onda
Spiegazione Rayleigh - Jeans
Un altro tentativo fu fatto da Lord Rayleigh e James Jeans: il loro risultato
riproduceva bene la curva di corpo nero alle grandi lunghezze d’onda, ma falliva alle
lunghezze d’onda corte e non mostrava nessun massimo di emissione
Spiegazione Planck
Nel 1900, Max Planck riesce a ricavare una formula che riproduce i valori
osservati nello spettro del corpo nero
Spiegazione Planck
Le pareti di una cavità contengono
particelle, che assorbendo energia
dall’esterno aumentano la loro
temperatura e quindi la loro energia
cinetica e iniziano a oscillare.
Oscillando emettono radiazione, ma questa
radiazione non può assumere valori qualsiasi.
L’energia deve essere emessa in quantità definite o
pacchetti.
Alle alte frequenze (piccole lunghezze d’onda) la
radiazione deve essere emessa in pacchetti più “grandi”.
Se le particelle non hanno abbastanza energia non si vedrà
emissione di radiazione ad alta frequenza
Se la temperatura aumenta, le particelle avranno
abbastanza energia per emettere pacchetti di
radiazione a frequenze via via più alte.
Spiegazione Planck
Qual è il legame fra la dimensione dei pacchetti (E) e la frequenza
della radiazione emessa (f) ?
lMAX »
1
Þ fMAX » T
T
Se la temperatura raddoppia, anche la frequenza a cui gli oscillatori
producono la massima energia raddoppia
Se la temperatura raddoppia anche la dimensione dei pacchetti di energia
emessa raddoppia
E = h× f
h = 6, 626 ×10-34 J × s