Dispositivi a stato solido

JFET e MESFET
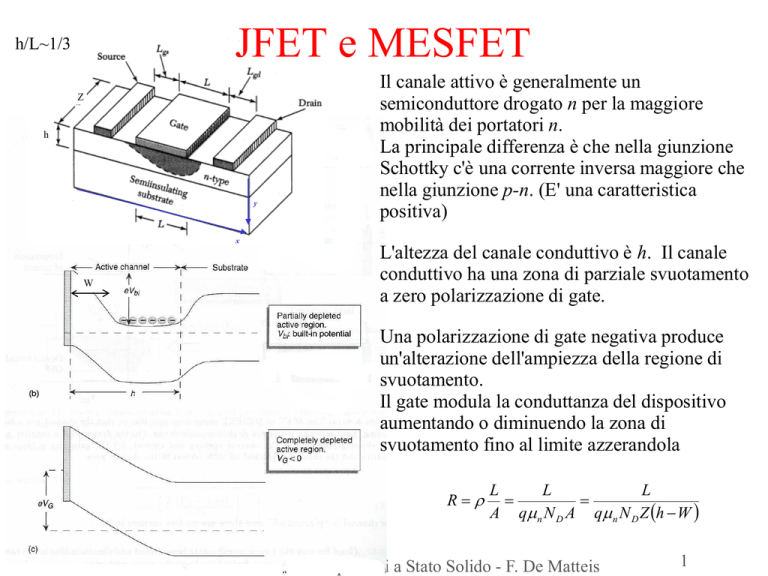
h/L~1/3
Z
h
y
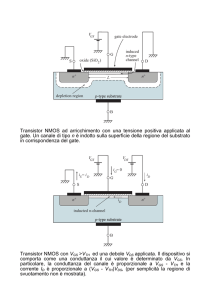
Il canale attivo è generalmente un
semiconduttore drogato n per la maggiore
mobilità dei portatori n.
La principale differenza è che nella giunzione
Schottky c'è una corrente inversa maggiore che
nella giunzione p-n. (E' una caratteristica
positiva)
x
W
L'altezza del canale conduttivo è h. Il canale
conduttivo ha una zona di parziale svuotamento
a zero polarizzazione di gate.
Una polarizzazione di gate negativa produce
un'alterazione dell'ampiezza della regione di
svuotamento.
Il gate modula la conduttanza del dispositivo
aumentando o diminuendo la zona di
svuotamento fino al limite azzerandola
R
LM Fisica A.A.2013/14
L
L
L


A q n N D A q n N D Z h  W 
Fisica dei Dispositivi a Stato Solido - F. De Matteis
1
Modulazione
del canale conduttivo
Z
h
 2 Vbi  VT  
h= 

eN d


1/ 2
VGS=VT polarizzazione di soglia per
inizio dello strozzamento
Vbi-VT=Vp tensione di strozzamento intrinseco
eN d h 2
Vp =
2
eN d h 2
VT = Vbi  V p = Vbi 
2
Se VP è minore del potenziale di costruzione Vbi , il canale del dispositivo è
completamento svuotato in assenza di polarizzazione di gate. Una polarizzazione
di gate positiva può aprire il canale.
Tali dispositivi sono detti in modo aumentato
Al contrario se VP è maggiore del potenziale di costruzione Vbi il canale è
parzialmente svuotato. Un a polarizzazione negativa del gate lo può svuotare
completamente.
Questi dispositivi funzionano in modalità di svuotamento
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
2
Caratteristiche corrente-voltaggio
Un analisi completa dell'andamneto della corrente è complicata (Eq
di Poisson e continuità della corrente risolta in maniera auto
consistente)
Disp4.ppt
Facciamo alcune approssimazioni.
y
La mobilità degli elettroni è costante e indipendente dal campo
elettrico. Vero solo per bassi campi. Per campi alti la velocità
satura. Limite 2-3 kV/cm, non eccessivamente alto. Al di sopra
sovrastimiamo e dovremmo dare una trattazione completa.
Approssimazione di campo graduale (Shockley). In assenza di
 dV  polarizzazione S-D l'ampiezza di svuotamento è quella solita W.
I D = Z h  W x   e N d μn  

 dx  In presenza di polarizzazione S-D dobbiamo assumere W(x).
Assumiamo che il campo lungo x sia minore del campo lungo h.
L'ampiezza W(x) è semplicemente determinata dal potenziale V(x)
Area
Densità di carica Campo
come se fosse costante (giunzione p-n) E' valida se L>>h
e mobilità
Sostituendo e integrando otteniamo
1

VDS 

L






2

V
x
+
V

V
1
2
bi
GS

I D = I D L = eμn N d Z   h  



eN d
 2 VDS x +Vbi  VGS  2

 
0
0

W x  = 



eN



d
Lgo
LM Fisica A.A.2013/14

3/ 2
3/ 2





2
V
+
V

V

V

V
DS
bi
GS
bi
GS
= eμn N d ZhVDS 

3 eN d h 2 / 2

Fisica dei Dispositivi a Stato Solido - F. De Matteis



3
Caratteristiche corrente-voltaggio

3/ 2
3/ 2





2
V
+
V

V

V

V
DS
bi
GS
bi
GS
I D = g o VDS 

3 Vp




Condizione di non-strizzamento
y
W L  =
2 VDS +Vbi  VGS 
<h
eN d
Quando il canale si strizza(in prima approssimazione) la corrente
di drain satura. V L  = V  V V  V
 dV 
I D = Z h  W x   e N d μn  

 dx 
y
bi
GS
DS
p
La tensione di drain a cui avviene la saturazione è
VDS sat  = V p  Vbi +VGS  0
V p VDS = 0  = Vbi  VT
E la corrente di saturazione è


3/ 2
3/ 2






2
V

V
+
V
+
V

V

V

V
p
bi
GS
bi
GS
bi
GS

=
I D sat  = g o V p  Vbi +VGS 


3 Vp


3/ 2
V p
2Vbi  VGS  

= g o   Vbi +VGS +
3
3 Vp


LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
4
Caratteristiche corrente-voltaggio
Il modo in cui il gate controlla la corrente di drain è rappresentata dalla
transconduttanza gm
dI
gm = D
dVGS
 V +V  V  V  V
bi
GS
= g o  DS bi GS

Vp
VDS const





g0 =
eμn N d Zh
L
La transconduttanza è aumentata in materiali con alta mobilità
e/o corte lunghezze di canale L
L'espressione per la corrente si semplifica se assumiamo
VDS<<Vbi-VGS REGIONE LINEARE
Sviluppiamo in serie di Taylor l'espressione della corrente ID

I D = g o 1 

Vbi  VGS  V
Vp


DS
gm =
g oVDS
2 V p Vbi  VGS 
In REGIONE DI SATURAZIONE invece

g m sat  = g o 1 

Vbi  VGS  
Vp


Tutto questo vale fino allo strozzamento, poi per spiegare la saturazione bisogna fare delle
opportune
assunzioni fisicheFisica dei Dispositivi a Stato Solido - F. De Matteis
5
LM
Fisica A.A.2013/14
Effetti in dispositivi reali
Diversi fattori devono essere presi in considerazione nei dispositivi reali che possono
modificare il comportamento fin qui esaminato.
Fondamentalmente le differenze derivano dall'assunzione che la mobilità dell'elettrone è
costante indipendentemente dal campo applicato.
In realtà si ha saturazione della velocità vs Come avevamo detto le correnti sono
sovrastimate. Diversi approcci sono stati adottati per correggere questo errore.
μn F
 Si assume v  F  =
I D0
μn F
1+
ID =
vs
μnVDS
1+
Questo risulta in una diminuzione della corrente di un fattore


vs L
Per piccoli dispositivi (≤1 m) assume che la velocità è sempre al valore di
saturazione
Si assume un modello a due regioni dove la mobilità è costante in una regione fino a
valori di campo inferiori a Fp e poi diventa costante vs
La questione è delicata e richiederebbe modelli bidimensionali che possono essere risolti
con approcci di calcolo numerico e con software dedicati estremamente sofisticati.
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
6
Modulazione della lunghezza del canale
Corrente è inversamente proporzionale alla lunghezza del canale L.

3/ 2
3/ 2

2 VDS +Vbi  VGS   Vbi  VGS 

I D = g o VDS 

3 Vp

L  L  DL  L'



g0 =
eμn N d Zh
L
gD =
I D
VDS
0
VGS
=cost
Lunghezza effettiva del canale
Quando si arriva a VDS(sat) il canale si strizza sul lato
del drain. Se VDS aumenta la zona di strozzamento si
allarga verso il source e il VDS(sat) è sopportato da
una lunghezza L' mentre sul resto DL=L-L' il
potenziale percepito è (VDS-VDS(sat) )
ΔL =
2 VDS  VDS sat 
eN d
1
1
ΔL 
Realisticamente questa lunghezza 1 =
  1+

1
L'
L
2
L


di svuotamento DL si estenderà in eff L  ΔL
2
egual misura nella regione del
canale e in quella del drain. Così
la diminuzione effettiva della
lunghezza del canale attivo è ~ ½
DL
LM Fisica A.A.2013/14
ΔL VDS  

I' D VDS > VDS sat  = I D sat  1 +

2
L


Fisica dei Dispositivi a Stato Solido - F. De Matteis
7
Effetto della modulazione del canale
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
8
Modello di risposta in frequenza
La carica DQ che si accumula sul Gate è la stessa
variazione che si genera nel canale. Se Dt è il tempo
impiegato dal dispositivo a rispondere a questo
cambiamento, possiamo definire una corrente dID
δQ
δI D =
Δt
gm =
I D
VGS
VDS
=cost
Il tempo Dt è il tempo impiegato mediamente dai portatori
per attraversare il dispositivo ttr
gm =
=
I D
Q
VDS
Q
VG
VDS
CG CGS  CGD

ttr
ttr
CG è la capacità gate-canale e
descrive la relazione tra
tensione di gate e carica di
gate
C'è poi la conduttanza di uscita gD che
descrive la dipendenza della corrente
di drain dal suo potenziale
gD =
I D
VDS
A completare il quadro ci sono poi le resistenze dei contatti ohmici RG, RD e RS e le capacità CDS
drain-substrato e CDC drain-canale e la resistenza del canale Rl
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
9
VGS
Modello di risposta in frequenza
Un'importante parametro che caratterizza i FET è la frequenza di cut-off di
guadagno di corrente diretta fT che definisce la massima frequenza al quale il
guadagno di corrente diventa unitario. Il fattore che limita la risposta del
dispositivo è il tempo di carica della capacità. Allora alla frequenza di cutoff la
corrente di gate Iin è uguale alla grandezza della corrente di uscita dal canale gmVGS
Iin = d/dt Qin = jw CG VGS = gmVGS
fT =
gm =
g oVDS
2 V p Vbi  VGS 

g m sat  = g o 1 

Vbi  VGS  
Vp
gm
1
=
2πCG 2πttr
Quindi la risposta in frequenza del dispositivo è ottimizzata usando materiali con migliori
proprietà di trasporto e minori lunghezze di canale.
Rimanendo nel modello di mobilità costante, il massimo valore della transconduttanza é
(prendendo Vbi = VGS):
eμn N d Zh h
ZL
C
=


f
max
=

T

Vbi  VGS   G
h
L
2ZL
g sat  = g 1 
m
o


= go =
Vp
eμn N d Zh
L


eμn N d h 2
fT max 
2πL2
L'espressione è sovrastimata per i limiti del modello a mobilità costante. Assumendo che i portatori si
muovono alla velocità saturata vs, il tempo di transito ttr è semplicemente L/vs
vs
fT max =
2πL
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
10


Scelta materiale
2/3 vs(InP)=vs(GaAs)=2 vs(Si)
LM Fisica A.A.2013/14
Fisica dei Dispositivi a Stato Solido - F. De Matteis
11
Applicazioni a grandi segnali analogici
Un importante utilizzo dei dispositivi FET è quello di
amplificazione di grandi segnali per amplificatori di
potenza.
In questo caso si fa operare il FET in regime di
saturazione. Il variare della polarizazione di gate fa
variare la polarizzazione di drain dalla tensione di
breakdown VB a VDS(sat).
La massima potenza di uscita è data da (media nel
tempo da cui il fattore 8 a denominatore)
Pm =
I m VB  VDS sat 
8
Si vorrebbe VDS (sat), il punto al quale la linea di carico interseca la regione lineare della curva I-V, più
basso possibile. Questo richiede materiali ad alta mobilità (GaAs) con bassa resistenza di source e di
drain.
Si vorrebbe anche una tensione di breakdown VB più alta possibile, e quindi la necessità di materiali ad
alta gap.
Un compromesso tra alto VB e alto ft per il dispositivo è dato da
VB fT  VB
LM Fisica A.A.2013/14
vs
F v
 crit s
2πL
2π
Fisica dei Dispositivi a Stato Solido - F. De Matteis
12