Trasformazioni
termodinamiche
Lo stato di un gas perfetto è descritto dall’equazione di
stato (PV = nRT = NkBT).
P = pressione del gas all’interno di un cilindro;
V = volume del gas;
T = temperatura del gas;
n = numero di moli di gas
R = 8,3144621 Jmol-1K-1 = Costante dei gas perfetti;
kB = 1,380648810-23 JK-1= Costante di Boltzmann
N = numero di particelle contenute nel cilindro.
Lo stato del sistema è conoscibile mediante due delle tre
variabili presenti nell’equazione.
Si abbia un cilindro contenente un gas. Le
grandezze che caratterizzano lo stato del gas sono
la pressione, P, il volume, V, e la temperatura, T.
Nel piano di Clapeyron lo stato del gas è
rappresentato da un punto.
Mediante interazione con l’ambiente circostante,
si fa evolvere il gas, il quale passa dallo stato A,
descritto dai parametri P1, V1 e T1, allo stato B,
descritto dai parametri P2, V2 e T2.
Nel passare dallo stato A allo stato B, il gas avrà
assunto infiniti stati fisici intermedi, successivi e
diversi, che costituiscono una trasformazione
termodinamica aperta.
Quindi quando un
sistema muta il
proprio stato fisico,
forzatamente o no,
subisce
una
trasformazione.
Ciclo termico
Quando il sistema, dopo una successione di diversi ed infiniti
stati intermedi, si riporta allo stato iniziale allora esso ha
subito una trasformazione chiusa o, più comunemente, un
ciclo termico.
2
1
Il gas, mediante una serie
di
trasformazioni
termodinamiche,
passa
dallo stato A allo B
seguendo il cammino 1.
Successivamente
passa
dallo stato B allo stato A
seguendo il cammino 2. I
due cammini, insieme ,
formano un ciclo termico.
Equilibrio di un sistema
Uno stato termodinamico (gas all’inyerno di un
cilindro) è caratterizzato dai valori dei parametri
volume, pressione e temperatura, legati
dall’equazione dei stato dei gas perfetti.
Quando su ogni punto del sistema la risultante
delle forze è nulla, allora il sistema si dice che è in
equilibrio meccanico, anche se può subire delle
variazioni chimiche.
Se non avvengono variazioni chimiche, allora il
sistema si dice che è in equilibrio chimico.
Equilibrio di un sistema
Se tutti i punti di un sistema si trovano alla stessa
temperatura si dice che è in equilibrio termico.
Se il sistema è contemporaneamente in equilibrio
meccanico, chimico e termico allora si dice che è
in equilibrio termodinamico.
Trasformazione quasi statica
Nel passare da uno stato, A, ad un altro, B, la
trasformazione deve essere quasi statica. Cosa
significa? Un gas si trova in equilibrio termico
quando in tutti i suoi punti la pressione e la
temperatura hanno gli stessi valori. Quando il gas
passa da uno stato ad uno vicinissimo, nel senso che i
valori della pressione,
del volume e della
temperatura sono variati di quantità infinitesime, i
due stati devono essere in equilibrio termico (quasi
statico). Ciò significa che il passaggio del gas dallo
stato A allo stato B deve avvenire in modo molto
lento.
Trasformazione reversibile
Il gas nel passare dallo stato A allo stato B, ha dovuto
interagire con l’ambiente circostante. Quest’ultimo ha pertanto
subito delle modifiche, poiché ha scambiato energia con il
sistema. Quindi nell’ambiente circostante è rimasta la traccia
della trasformazione.
Trasformazione reversibile
Successivamente, al sistema si fa compiere una
trasformazione che lo porti dallo stato B allo stato A
percorrendo a ritroso il cammino, cioè passando per gli stessi
stati.
Se
quest’ultima
trasformazione
riesce
a
cancellare la traccia lasciata
nell’ambiente
circostante
dalla prima trasformazione,
allora la trasformazione è
detta
reversibile.
Una
trasformazione reversibile è
una trasformazione ideale e
non reale.
Trasformazioni irreversibili
Se, invece, l’ambiente circostante contiene traccia lasciate
dal sistema nel compiere le due trasformazioni, allora le
trasformazioni si dicono irreversibili.
Le trasformazioni irreversibili sono quelle reali che si
verificano in natura. Considerando un gas all’interno di un
cilindro, la traccia è, nel caso reale, l’attrito tra la parete
del cilindro ed il pistone.
Altro esempio: Se la sorgente di calore è una fiamma
ottenuta facendo bruciare del combustibile (ambiente
circostante), dopo la trasformazione l’ambiente circostante
è cambiato poiché all’inizio si aveva il combustibile, al
termine sia hanno fumi ed altri prodotti di combustione.
Trasformazioni reversibili ed irreversibili
Quindi in un sistema chiuso (il sistema scambia
energia ma non materia con l’ambiente
circostante) a composizione chimica costante,
senza azioni elettromagnetiche, le condizioni
necessarie e sufficienti alla reversibilità sono:
assenza di attriti, equilibrio fra le pressioni e fra
le temperature interne ed esterne.
Processi irreversibili
In natura tutte le trasformazioni spontanee sono
irreversibili. Ogni processo spontaneo, che avviene in
natura, corrisponde al passaggio di un sistema da una
posizione di disequilibrio ad una situazione di equilibrio.
Il verso naturale dell’evoluzione di un sistema non è
arbitrario ma tende ad evolvere da situazioni in cui i
molti corpi, che compongono il sistema, presentano
diversi valori nelle grandezze fisiche verso situazioni in
cui questi valori sono uniformizzati, cioè tutti uguali.
Processi irreversibili
Pertanto il sistema che evolve spontaneamente non può
più tornare spontaneamente indietro. Allora si dice che un
processo spontaneo una volta avvenuto è irreversibile. In
generale, un processo si definisce irreversibile quando
gli effetti del processo sul sistema e sul suo ambiente non
possono essere cancellati.
Processi irreversibili
Principali categorie di processi irreversibili sono tutti i
processi in cui interviene l’attrito, l’espansione libera,
passaggio di calore dovuto a una differenza di
temperatura, combustione, diffusione per mescolamento
di due fluidi di diversa composizione oppure diversa
pressione o temperatura. Dato che nessun processo in
natura è completamento esente dai fenomeni sopracitati,
tutti i processi reali sono in qualche misura irreversibili.
Ciclo termico
Un ciclo termico si dice reversibile se sono reversibili
tutte le trasformazioni che lo compongono.
Invece, se almeno una trasformazione è irreversibile,
allora tutto il ciclo è irreversibile.
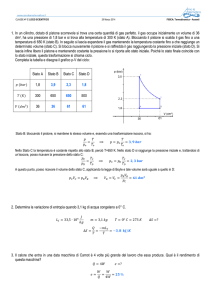
Lavoro in una trasformazione termodinamica
Un gas, nel subire una trasformazione termodinamica,
passa da uno stato descritto dai parametri P1, V1 e T1, ad
uno stato i cui parametri sono P2, V2 e T2.
Nel caso descritto
dalla figura, il gas si
espande e cambia il
suo volume
V V2 V1
Lavoro in una trasformazione termodinamica
Il pistone si alza a causa della pressione, P, che viene
esercitata sulla sua base.
F
F
Per definizione, la
pressione, P, è il
rapporto tra la forza,
F, esercitata dal gas
alla base del pistone e
la superficie, S, del
pistone.
F
P
S
Lavoro in una trasformazione termodinamica
La forza, F, che il gas esercita sul pistone è:
F Pr essione sup erficie P S
F
F
La forza, F, viene
applicata per un tratto di
cammino pari ad h e
compie
un
lavoro
elementare pari a L.
Lavoro in una trasformazione termodinamica
Il lavoro, L, che il gas nel’espandersi compie
sull’ambiente circostante è:
L Forza spostament o F s F h
Elaborando si ha:
F
F
L P S h P S h
Dove l’espressione Sh è
la variazione di volume
subita dal gas:
S h V V2 V1
Lavoro in una trasformazione termodinamica
In conclusione, il lavoro elementare fatto dal gas è:
L P S h P S h P V P V2 V1
F
F
In una espansione il
lavoro è positivo poiché
il volume finale è
maggiore del volume
iniziale, V2>V1.
Lavoro in una trasformazione termodinamica
Se il pistone si abbassa si ottiene una compressione. Ciò
significa che il lavoro è stato compiuto dall’ambiente
circostante sul sistema-gas.
Festerna
Festerna
In una compressione
il lavoro è negativo,
poiché il volume
finale è minore del
volume
iniziale,
V2<V1.
L P S h P V2 V1 0
Lavoro in una trasformazione termodinamica
Se il pistone si abbassa si ottiene una compressione. Ciò
significa che il lavoro è stato compiuto dall’ambiente
circostante sul sistema-gas.
Festerna
Festerna
In una compressione
il lavoro è negativo,
poiché il volume
finale è minore del
volume
iniziale,
V2<V1.
L P S h P V2 V1 0
Lavoro – grafico
Si considera una trasformazione che porta il gas dallo stato A
(P1, V1, T1) allo stato B (P2, V2, T2). Nella espansione il gas
compie un lavoro dell’ambiente circostante. Il lavoro vale:
L=PV.
In riferimento al grafico,
geometricamente
il
prodotto PV non è
altro che l’area di un
rettangolo; ovvero, in
senso generale, è l’area
(colore giallo) della
porzione di piano che si
trova sotto la curva della
trasformazione.
Lavoro – grafico
Quindi se nel piano di Clapeyron, P-V, è rappresentato una
trasformazione termodinamica, il lavoro fatto dal gas
sull’ambiente circostante oppure dall’ambiente sul gas si ricava
calcolando l’area sotto la curva della trasformazione
termodinamica.
Ciclo termico – grafico
Un ciclo termico è una successione di trasformazioni
termodinamiche che riportano il gas allo stato iniziale. Se il gas si
trova, all’inizio, nello stato A, dopo una serie di trasformazioni, che
sono sintetizzate rappresentate dai cammini 1 e 2, il gas ritorna allo
stato iniziale A.
I due cammini, 1 e 2,
delimitano una regione
finita di piano.
Ciclo termico – grafico
Graficamente si nota che le trasformazioni si susseguono in senso
orario.
Quando si verifica questa situazione, il lavoro è
positivo ed è fatto dal gas sull’ambiente circostante.
Inoltre, graficamente, il
valore del lavoro si trova
calcolando
l’area
racchiusa dal ciclo, ovvero
l’area del piano racchiusa
tra i due cammini 1 e 2
(parte gialla del grafico.)
Ciclo termico – grafico
Se le trasformazioni si susseguono in senso antiorario, allora
il lavoro è negativo ed è fatto dall’ambiente circostante sul
gas.
Anche
in
questa
situazione, il valore
del lavoro si trova
calcolando
l’area
racchiusa dal ciclo,
ovvero l’area del
piano racchiusa tra i
due cammini 1 e 2
(parte
gialla
del
grafico.)
Trasformazione isobara
Un gas, contenuto in un recipiente, subisce una
trasformazione isobara quando la sua pressione si
mantiene costante, mentre la sua temperatura ed il suo
volume variano. La legge di Gay-Lussac che regola tale
trasformazione è la seguente:
V nR N k
=
= costante
T
P
P
V1 V2 n R N k
=
= costante
T1 T2
P
P
Se
P1V
,V
e T1 sonole
Se P,
1 1e T1 sono
le
condizioni
iniziali,
condizioni
iniziali,
e
eP,PV2,2 V
T2 le
e 2Te2 le
condizioni
condizioni finali,
finali, con
alloraPl’equazione
= P = P è:
1
2
allora l’equazione è:
Trasformazione isobara
Un gas perfetto è contenuto in un cilindro ed all’inizio si
trova nello stato A, descritto dai parametri P=P1, V1 e T1. Il
cilindro è poggiato sul termostato che si trova alla
temperatura T1.
Trasformazione isobara
Successivamente si mette a contatto il cilindro con un secondo
termostato che si trova alla temperatura T2. Il gas assorbe calore e
l’energia cinetica media delle particelle aumenta. Poiché la pressione
si mantiene costante, il gas si espande aumentando il suo volume. Il
nuovo stato B del gas è descritto dai seguenti parametri: P=P2, V2, T2.
Trasformazione isobara
Nel piano di Clapeyron, la trasformazione isobara è
rappresentata nel grafico da un segmento, [AB], parallelo
all’asse del volume.
Nel grafico il gas si
espande ed il lavoro è
positivo ed è fatto dal gas
sull’ambiente circostante.
Se il verso fosse stato
opposto (compressione), il
lavoro
sarebbe
stato
negativo.
Trasformazione isobara
Nel caso in esame, il gas si espande, il pistone si alza e
viene compiuto un lavoro dal sistema sull’ambiente
circostante. Il lavoro che viene compiuto per portare il gas
dallo stato iniziale A allo stato finale B è:
L AB P V P V2 V1
La misura dell’area sotto
il segmento [AB] è il
lavoro fatto dal gas
sull’ambiente circostante.
Trasformazione isobara
Il calore che il gas assorbe vale:
Q n cp T2 T1
dove:
n = numero di moli
cP = calore specifico del gas a pressione costante
Trasformazione isobara
Applicando alla trasformazione isobara il primo principio
della termodinamica, la variazione di energia interna, U,
è:
U Q L n cp T2 T1 P V2 V1
dove:
n = numero di moli
cP = calore specifico del gas a pressione costante
Trasformazione isocora
L’isocora è una trasformazione in cui il volume si mantiene
costante, mentre la pressione e la temperatura variano. La
legge che regola tale trasformazione è la seguente:
P n R N k
=
= costante
T
V
V
Se
Se P
P11,, V
V11 ee T
T11 sono
sono le
le
condizioni
condizioni iniziali,
iniziali, ee P
P22,,
V
V22 ee T
T22 le
le condizioni
condizioni
finali,
finali, con
con
V
V11=V
=V22=V
=V
P1 P2 n R N k
=
= costante
allora
allora l’equazione
l’equazione è:
è:
T1 T2
V
V
Trasformazione isocora
Un gas perfetto è contenuto in un cilindro ed all’inizio si
trova nello stato A, descritto dai parametri P1, V1=V e T1. Il
cilindro è poggiato sul termostato che si trova alla
temperatura T1.
Trasformazione isocora
Successivamente si mette a contatto il cilindro con un secondo
termostato che si trova alla temperatura T2. Il gas assorbe calore e
l’energia cinetica media delle particelle aumenta. Poiché il volume si
mantiene costante, il gas né si espande né si comprime. Il nuovo stato
B del gas è descritto dai seguenti parametri: P2, V2=V, T2.
Trasformazione isocora
Nel piano di Clapeyron, la trasformazione isocora è
rappresentata nel grafico da un segmento, [AB], parallelo
all’asse della pressione.
Trasformazione isocora
Nel caso in esame, il pistone né si alza né si abbassa, a
causa delle dimensioni inalterate del cilindro+pistone, per
cui il lavoro è nullo.
L AB 0
Trasformazione isocora
Il calore che il gas assorbe vale:
Q n c V T2 T1
dove:
n = numero di moli
cV = calore specifico del gas a volume costante
Trasformazione isocora
Applicando alla trasformazione isocora il primo principio
della termodinamica, la variazione di energia interna, U,
è:
U Q L n c V T2 T1
dove:
n = numero di moli
cV = calore specifico del gas a pressione costante
Trasformazione isoterma
Una isoterma è una trasformazione in cui la temperatura del
gas si mantiene costante. La legge, detta di Boyle-Mariotte,
che regola tale trasformazione è la seguente:
P V = n R T N k T = cost
Se P1, V1 e T1 sono le condizioni iniziali, e P2, V2 e
T2 le condizioni finali, con
T1=T2=T
allora l’equazione è:
P1 V1 = P2 V2 n R T N k B T cost
Trasformazione isoterma
Un gas perfetto è contenuto in un cilindro ed all’inizio si
trova nello stato A, descritto dai parametri P1, V1 e T1=T. Il
cilindro è poggiato sul termostato che si trova alla
temperatura T1.
Trasformazione isoterma
Il gas, messo a contatto con il termostato, che si trova a temperatura
T, scambia calore. Poiché la temperatura deve rimanere costante, il
calore scambiato deve essere convertito interamente in lavoro
meccanico.
Trasformazione isoterma
Se il gas assorbe calore e si espande. Il volume aumenta
(espansione), il lavoro è fatto dal sistema sull’ambiente circostante, e
la pressione diminuisce.
Trasformazione isoterma
Se avviene una compressione, il volume diminuisce, il
lavoro è fatto dall’ambiente circostante sul sistema, la
pressione aumenta ed il sistema cede calore alla sorgente
Trasformazione isoterma
Il nuovo stato, A, del gas è descritto dai seguenti parametri:
P2,
V2,
T2 = T (costante)
Trasformazione isoterma
Nel piano di Clapeyron, la trasformazione è rappresentata
da un ramo di iperbole equilatera.
Trasformazione isoterma
La temperatura costante implica che l’energia interna
del sistema rimanga costante. Pertanto:
U 0
Dal primo principio della termodinamica (U=Q-L) si
deduce che:
QL
Trasformazione isoterma
V2
L = n R T ln
V1
Il lavoro compiuto dal gas è:
Dalla legge di Boyle-Mariotte si ha che:
P1 V1 P2 V2
P1 V2
P2 V1
pertanto:
V2
P1
L = n R T ln
n R T ln
V1
P2
Trasformazione adiabatica
Una trasformazione è adiabatica se il sistema non
scambia calore con l’ambiente circostante, cioè non è a
contatto con nessuna sorgente di calore.
L’equazione che regola una trasformazione adiabatica è
l’equazione di Poisson:
P V costante
Trasformazione adiabatica
Varianti dell’equazione sono:
TV
T
1
1
TP
costante
P costante
1
costante
T P
T
1
1
1
costante
V costante
Trasformazione adiabatica
Il fattore γ che compare nelle formule si chiama indice
adiabatico. Il suo valore è:
cP
cV
dove cP e cV sono rispettivamente il calore specifico a
pressione costante ed il calore specifico a volume
costante.
Trasformazione adiabatica
Il valore dei calori specifici, cP e cV, dipendono dalla struttura
molecolare delle particelle che compongono il gas.
Per un gas monoatomico, come l’elio, il neon, l’argon, i
valori dei calori specifici sono:
3
cV R
2
5
cP R
2
Dove R è la costante dei gas perfetti. Dalle due
equazioni si ha che:
cP cV R
Trasformazione adiabatica
Per molecole biatomiche, come l’idrogeno,
l’ossigeno, i valori dei calori specifici sono:
5
cV R
2
7
cP R
2
l’azoto,
Trasformazione adiabatica
L’indice adiabatico, γ, per un gas monoatomico è:
5
R
cP 2
5
cV 3 R 3
2
L’indice adiabatico, γ, per un gas biatomico è:
7
R
cP 2
7
cV 5 R 5
2
Trasformazione adiabatica - grafico
Un cilindro è poggiato su di un supporto isolate (non scambia
calore) è le sue condizioni iniziali sono: P1, V1, T1.
Meccanicamente si fa
compiere
una
espansione al gas. Le
condizioni
finali
sono: P2, V2, T2.
Trasformazione adiabatica - grafico
Nel piano di Clapeyron la trasformazione adiabatica è una
curva che interseca delle isoterme (quindi la curva non è un
ramo di iperbole). L’equazione che descrive una adiabatica
è:
P V costante
P1 V 1 P2 V2 cost
Trasformazione adiabatica - energia
Nella trasformazione adiabatica non vi scambio di calore, per
cui si ha:
Q0
Pertanto applicando il primo principio della termodinamica si
ha:
U L
Trasformazione adiabatica - energia
Osservazione: Se il gas si espande, il sistema compie un
lavoro sull’ambiente circostante, cioè il lavoro è positivo.
Dal primo principio si deduce che l’energia interna
diminuisce. Poiché l’energia interna è collegata alla
temperatura, questa diminuisce.
Se si ha una compressione il lavoro è fatto dall’ambiente
circostante sul gas. Il lavoro è negativo e la variazione di
energia interna è positiva. Di conseguenza la temperatura
aumenta.
L 0 U 0 Temperatur a dim inuisce
L 0 U 0 Temperatur a aumenta
Trasformazione adiabatica - lavoro
Adoperando l’equazione di Poisson si calcola il lavoro
fatto dal o sul sistema che è uguale a:
P1 V1 1
1 n R T1 V1
L=
- -1
1
-1
- 1 V1
1
V2
V2
Alcune varianti del lavoro sono:
1
L=
P1 V1 - P2 V2
-1
L = n c V R T2 T1
L’ultima espressione è la più semplice.
1
Energia interna – funzione di
stato
Sulla energia interna è opportuno effettuare un
approfondimento.
In un gas perfetto l’energia interna è associata alla
temperatura; cioè la variazione di energia interna è
associata alla variazione di temperatura.
U interna
3
3
= N Ec = N k T = n N A k T
2
2
Energia interna – funzione di stato
Si considera un gas perfetto che si trova nello stato A
caratterizzato dalle variabili termodinamiche P1, V1, T1.
Mediante
scambi
energetici (calore e
lavoro) si fa evolvere
il gas verso uno stato
B caratterizzato dalle
variabili
termodinamiche P2,
V2, T2.
Energia interna – funzione di stato
In quanti modi può evolvere il gas nell’andare dallo stato
A allo stato B? Vi sono infiniti modi.
Nella figura
è
rappresentato
uno
degli infiniti cammini
che portano il gas
dallo stato A allo stato
B.
Energia interna – funzione di stato
Nella figura sono rappresentati altri due cammini, 2 e 3,
che portano il gas dallo stato A allo stato B.
Energia interna – funzione di stato
In tutti e tre i cammini, la variazione di temperatura,
T=T2-T1, è la stessa. Ciò significa che anche la
variazione di energia interna, U, è la stessa.
Energia interna – funzione di stato
Quindi la variazione di
energia interna, U,
non dipende dal tipo
di cammino che ha
dovuto compiere il gas
per andare dallo stato
A allo stato B, ma
dipende solo dallo
stato iniziale, A, e
dallo stato finale, B.
Energia interna – funzione di stato
Una grandezza fisico-matematica, che soddisfa alla
condizione che la sua variazione dipende solo dallo
stato iniziale e finale, ma non dipende da come si è
evoluto nell’andare dallo stato iniziale e finale, si
chiama funzione di stato.
Quindi l’energia interna è una funzione di stato
Energia potenziale – funzione di stato
Altro esempio: In una regione in cui è presente
l’interazione gravitazionale ed in assenza di attrito, la
variazione di energia potenziale subita da un corpo, che
si sposta da un punto ad un altro, dipende solo dalla
posizione iniziale e finale occupata dal corpo ma non dal
cammino che ha dovuto compiere per andare dalla
posizione iniziale e finale. Ebbene, l’energia potenziale
gravitazionale è una funzione di stato.
Anche l’energia potenziale elettrica è una funzione di
stato.