Motore asincrono

MOTORE ASINCRONO
Allievi Meccanici
Motore asincrono
Campo rotante, circuito equiv.nte,
caratt.ca meccanica, avviamento
e regolazione
Un sistema elettromeccanico
Se il rotore ruota con
velocità  r
c
Rotore fermo
   M cos c t
d
e
  M  c sin  c t
dt
   M cos(c  r )t
e   M (c  r ) sin( c  r )t
Scorrimento
c   r
s
c
Genesi statica campo rotante;
avvolgimento trifase concentrato
i1  I M cos(t )
i2  I M cos(t  120) i3  I M cos(t  240)
Poli creati da un avvolgimento
monofase concentrato
Campo creato da un avvolgimento
monofase concentrato
Legge di Ampére
Nel caso di N spire in serie di un
avvolgimento attraversate dalla corrente i
e concatenate con λ, si ha:
H

t
dl


Ni


Se supponiamo  ferro   nel ferro si ha:
H 0
Campo magnetico creato da un
avvolgimento concentrato
H  tdl
su linea a →
H 2  H1  0  H 2  H1
su linea b
H 2  H1   Ni
H 2  H1   Ni / 
Su linea c
H 2  H1  Ni 
H 2  H1  Ni / 

Campo magnetico creato da un
avvolgimento concentrato
Il diagramma di H (componente di H
secondo la normale entrante nella superf.
interna di statore) a meno di μ0 fornisce
anche l’analoga compon.te B di B nel
traferro Tale diagramma è definito a meno
di una costante poiché deriva da
un’integrazione. La posizione di tale
diagramma rispetto all’asse delle ascisse
può essere dedotta considerando la
soleoinodalità di B .
Campo magnetico creato da un
avvolgimento concentrato
Per la soleinodalità di B il flusso dello stesso
uscente dalla superficie chiusa S costituita dalla
superficie interna di statore e dalle sue basi
frontali è nullo:

 
 B  ndS  RL0  Hd  0
S

Il valore medio di B o di H è quindi nullo.
R e L sono il raggio e la lunghezza della
superficie interna di statore
Campo magnetico creato da un
avvolgimento concentrato
Campo magnetico creato da un
avvolgimento concentrato
I sinusoidale i  I M cos t
Ni 4
B  0
cos   BM cos t cos 
2 
BM   0
NI M 2
 
Campo magnetico creato da un
avvolgimento concentrato
L’avvolgim.to crea un
campo a distribuzione
spaziale sinusoidale.
I massimi delle
semionde positiva e
negativa coincidono
con la mezzeria dei
poli sud e nord.
L’asse neutro (B=0)
con il piano dello
avvolgim. concentrato
Campo magnetico creato da un
avvolgimento distribuito
Campo magnetico creato da un
avvolgimento distribuito
Avvolgimento concentr.
NS IM 2
BM   0
 
N S numero di spire in
serie=N condut. x cava
Avvolgim. distribuito
B=B1+B2+B3→
K w N S I M 2 dove
BM   0

B  BM cos t cos 

Kw fattore d’avvolg.<1 e
N S  3N
Campo magnetico creato da un
avvolgimento distribuito
Il fattore di avvolgimento Kw dato da:
ampiezza ( B1  B2  B3 )
Kw 
ampiezza (3B2 )
consente di sostituire un avvolgimento
distribuito di N S spire con un avvolgimento
concentrato equivalente di K w  N S spire
Avvolgimento distribuito trifase
Genesi statica campo rotante;
avvolgimento trifase (1 N e 1 S)
i1  I M cos(t )
i2  I M cos(t  120) i3  I M cos(t  240)
Calcolo campo risultante
Il campo risultante deriva dalla somma dei
3 campi pulsanti di ciascuna fase
B( , t )  B1 ( , t )  B2 ( , t )  B3 ( , t )
B1 ( , t )  BM cos t cos 
B2 ( , t )  BM cos(t  120) cos(  120)
B3 ( , t )  BM cos(t  240) cos(   240)
Calcolo campo risultante
Applicando la relaz.ne trigonometrica
si ottiene:
1
cos( a) cos(b)  [cos( a  b)  cos( a  b)]
2
B( , t )  B1 ( , t )  B2 ( , t )  B3 ( , t )  B' ( , t )  B" ( , t ) dove
1
B' (  , t )  BM [cos(t   )  cos(t   )  cos(t   )] 
2
3
 BM cos(   t )
2
1
B" (  , t )  BM [cos(t   )  cos(t    240)  cos(t    480)]  0
2
3
 B(  , t )  BM cos(   t )
2
Campo rotante (Teorema di Galileo
Ferraris)
La relazione:
3
B(  , t )  BM cos(   t )
2
esprime il teorema di
Galileo Ferraris e
rappresenta un campo
rotante. Lo spostam. 
tra le curve (1) e (2) nel
tempo t è tale che:

  t  0   c 

t
 c è la velocità del
campo rotante
3
(1)  BM cos(  )
2
(2) 
3
BM cos(   t )
2
Coppie polari p > 1
Num. di poli=num. di semi onde=2p
B  BM cos t cos p
Campo rotante per p>1
Teorema di G. Ferraris
3
B(  , t )  BM cos( p  t )
2
Lo spostam.  tra le
curve (1) e (2) nel
tempo t è tale che:
 
p  t  0   c 

t
p
3
(1)  BM cos( p )
2
3
(2)  BM cos( p  t )
2
Teorema di Galileo Ferraris
3
B(  , t )  BM cos( p  t )
2
Rappresenta una distribuzione di p onde
sinusoidali (corrispondenti a p poli Nord e a p
poli Sud) viaggianti in senso orario lungo il
traferro con velocità angolare:
c 

p
[rad / sec]
Velocità del campo rotante
Esprimendo la velocità  c in giri al minuto:
 2f 2nc [rad / sec]
c  

p
si ottiene per nc
p
60
:
nc  60 f / p
[giri/min]
 c e nc vengono dette velocità di sincronismo del
motore. Se f=50 Hz si ha:
nc  3000 / p
se p=1 o p=2 o p=3 si ha rispettivamente
nc =3000 o 1500 o 750 giri al minuto
Flusso e f.e.m nello statore per
effetto del campo rotante
Flusso concatenato con una spira ϒ della fase 1
 /2p
 
3
(dS  RLd  )
    B  ndS  BM RL  cos( p  t )d
2
S
 / 2 p
1


     M [sin(  t )  sin(   t )]   M cos t
2
2
2
 M  RLBM 3 / p
La f.e.m. e indotta nella stessa spira è data da:
d 
e
  M sin t
dt
dove
Flusso e f.e.m nello statore per
effetto del campo rotante
La velocità relativa tra campo rotante e statore è ωc e la
pulsazione della f.e.m. e è data dal prodotto di tale
velocità relativa per p e cioè da ω=pωc.
Analogamente si calcolano il flusso e la corrispondente
f.e.m. per le fasi 2 e 3.
I flussi concatenati con una spira delle fasi 1,2 e 3
costituiscono una terna simmetrica diretta; anche le
corrispondenti f.e.m. costuiscono una terna simmetrica
diretta.
Il funzionamento del motore
Tipologie di rotore
Motore a rotore avvolto
Motore a gabbia
Motore a doppia gabbia
Il numero di poli del rotore
Il numero di poli del rotore nel caso di
motore a gabbia semplice e doppia è
eguale a quello dello statore, poiché
nell’avvolgimento rotorico i poli sono
automaticamente indotti dal campo rotante
statorico. Nel caso del rotore avvolto il
numero di poli è determinato dalle
modalità con cui sono collegati tra loro i
conduttori nelle cave e quindi può essere
anche diverso da quello di statore.
Funzionamento a macchina
ferma
Flusso e f.e.m nel rotore a
macchina ferma
Il campo rotante produce un flusso di B
concatenato con una spira della fase 1 di
rotore, supposta allineata con quella di
statore, ancora dato da:
    M cos t
dove  M  RLBM 3 / p
avendo supposto il numero delle coppie
polari del rotore eguali a quello dello statore.
La pulsazione della fem (-dφϒ/dt) è ancora
pari a ω.
Effetti delle f.e.m. nello statore e
nel rotore a macchina ferma
Il campo rotante statorico induce nello statore e
nel rotore le f.e.m, espresse nel dominio dei
fasori:
E S   jN S K ws 
E R   jN R K wR 
dove  è il flusso concat. con una spira,N S e N R
le spire in serie per fase di statore e rotore,K wS e K wR
i corrispondenti fattori d’avvolgimento. Le f.e.m
indotte fanno circolare correnti nell’avvolgimento
rotorico polifase, che, come nello statore,
costituiscono un sistema simmetrico diretto%
Effetti delle f.e.m. nello statore e
nel rotore a macchina ferma
→nasce un campo rotante di reaz. avente la stessa
velocità e lunghezza d’onda di quello statorico, se il
numero di poli di statore e rotore sono eguali. I due
campi rotanti sono pertanto sommabili e il campo
risultante, sostenuto dalle correnti statoriche e
rotoriche, ruota con la stessa velocità ωc. Si ha
pertanto un accoppiamento trasformatorico tra
statore e rotore. Le LKT di fase sono identiche a
quelle del trasformatore in corto circuito
V S  (rS  jlS ) I S  E S
0  (rR  jlR ) I R  E R
Effetti delle f.e.m. nello statore e
nel rotore a macchina ferma
che sono rappresentate da un circuito equiv. analogo a
quello del trasformatore. In tali equazioni:
rS è la resistenza di fase dell’avvolgimento statorico;
lS l’induttanza di dispersione di fase dell’avvolgimento
statorico;
rR la resistenza di fase dell’avvolgimento rotorico;
lR l’induttanza di dispersione di fase dell’avvolgimento
rotorico.
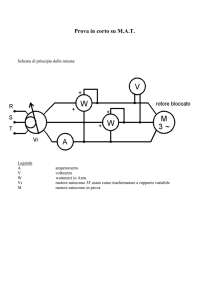
Circuito equivalente a rotore fermo
IS
rS
lS
VS
ES
N S K wS
ES
a
N R K wR
ER
r' R
I 'R
Lm
l 'R
Rm
rapp. di trasformaz.
Lm induttanza principale di statore Rm porta in conto le Pfe
I 'R  I R / a
r ' R  rR a
2
l 'R  lR a 2
Funzionamento a macchina in
movimento
Un sistema elettromeccanico
Se rotore ruota con
velocità  r
c
Rotore fermo
   M cos c t
d
e
  M  c sin  c t
dt
   M cos(c  r )t
e   M (c  r ) sin( c  r )t
Scorrimento
c   r
s
c
F.e.m in un motore con p coppie
polari
Si è già visto che il flusso concat. con una
spira dello statore e la f.e.m. in essa
hanno una pulsazione data dal prodotto
della velocità relativa tra campo rotante e
stat. per il numero di coppie polari p dello
statore ( p c   ) . Un risultato analogo
vale per il rotore.
Campo di reazione rotorico
Se il numero di coppie polari del rotore è
eguale a quello dello statore p, la pulsaz.
delle f.e.m. indotte nel rotore è data da

 
c 
p(c   r )  s dove s 

p
Se l’avvolgimento del rotore è polifase
nasce un campo rotante di reazione
rotorico, la cui velocità rispetto al rotore è
s
s
ed allo statore
%
  r  c
c
r
c
p
p
Campo di reazione rotorico
I due campi statorico e rotorico hanno la
stessa lunghezza d’onda e ruotano con la
stessa velocità rispetto allo statore. Si avrà
quindi un campo rotante risultante , che si
potrà sempre esprimere come:
3
B(  , t )  BM cos( p  t )
2
dove BM è sostenuto sia dalle correnti di
statore che di rotore.
F.e.m. risultanti
La f.e.m. risultante nello statore è data da:
E S   jN S K ws 
La analoga f.e.m. nel rotore è data da:
E R   jsN R K wR   s E R (1)
L’operatore jsω rappresentativo della d/dt
evidenzia che i fasori relativi al rotore
rappresentano grandezze di pulsazione
sω.
Reti equivalenti di statore e rotore
rS
jlS
IR
rR
IS
VS
jLm
Rm
E S   jN S K ws 
ES
jslR
s E R (1)
s E R (1)   jsN R K wR 
Rete equivalente di rotore
IR
IR
rR
jslR
s E R (1)
s E R (1)  (rR  jslR ) I r
E R (1)   jN R K wR 
E R (1)
rR
s
jlR
E R (1)  (rR / s  jlR ) I r
Rete equivalente di rotore
IR
IR
rR
s
E R (1)
jlR
rR
E R (1)
rR
1 s
 rR  rR
s
s
jlR
rR
1 s
s
Circuito equivalente a T
I SI S rS rS
VS
N S K wS
ES
a
N R K wR
ER
I 'R  I R / a
lSjl
I ' R I ' R r'r'R R
S
EjSLm
Lm
jl 'l'RR
r'R
Rm Rm E S
rapp. di trasformaz.
r ' R  rR a
2
l 'R  lR a
2
1 s
s
Simboli circuitali motore asincrono



Bilancio delle potenze
r' R
rS
IS
Pass
Rm
r'R
1 s
s
Pmecc
Bilancio delle potenze
Pot. Ass. 3VS I S cos  S
PJS  3rS I S2
r'R 2
I 'R
Pot. Sinc. PS  3
s
PJR  3r ' R I ' 2R  sPS
Pav  perd .attrito, ventilaz
PJR
s
PS
Pot. Mecc.  PS  PJR  (1  s) PS
1 s 2
 3r ' R
I 'R
s
Put  Pmecc  Pav
Rendimento del motore
Il rendimento è dato da
Put
Put


Pass Put  Pcu  P0
dove
Pcu  Pjs  Pjr
e P0 è la pot.za a vuoto
Pav  perd .attrito, ventilaz
P0  Pfe  Pav
Piccole mot. η=0,75
Grandi mot. η=0,95↔0,97
Coppia elettromeccanica
C. elettromecc.
 Cem 
PS
c
C em 
Pmecc
r
 C em
I 'R 
VS
r'R
 jx' R
s

2f
c  
p
p
r'R 2
dove PS  3 I ' R
s
3 p r'R 2 k r' 2

I 'R 
I 'R
2f s
f s
dove x' R  l 'R
r  (1  s)c
Pmecc  (1  s) PS
3p
k
2
dove
 
I '  I 'R
2
R
2
VS2

(
 Cem
sVS2
kr' R

f r ' 2R  s 2 x' 2R
r'R 2
)  x' 2R
s
Coppia elettromeccanica
C=Cem. Per calcolare
Cmax si pone
r'R
C
 x' R
0 
s
s
2
V
k
r'R
S

C

 s* 
M
f x' R
x' E
Cmax indip. da r' R
Tratto APO stabile
Tratto AQB instabile
s* scorrimento di
rovesciamento
Coppia elettromeccanica al variare
della resistenza rotorica
r' R
s'*
s' '*
s' ' '*
Punto di lavoro sulla caratteristica
coppia scorrimento
CN
P
C em
Cr
P punto di lavoro
intersez. tra caratt.
del motore e della
coppia resistente del
carico meccanico.
Capac. di sovracc.co
è data dal rapp.to tra
la coppia massima CM
e la coppia nominale C N
Punto di lavoro sulla caratteristica
coppia scorrimento
Il punto di lavoro si trova sul tratto stabile
della caratteristica C-s. Tale tratto è quasi
verticale (rigidità della caratterica C-s→
velocità quasi costante al variare del
2
C

f
(
V
) →
carico). em
un calo di
tensione determina un calo della capac. di
sovraccarico e può portare P sul tratto
instabile.
Caratteristica coppia velocità
n ed nc num. di giri al
minuto del motore e del
campo rotante (veloc.
sincronismo).
C em
1, nc
1  s, n
r  (1  s)c
n  (1  s)nc
60 c 60 f
nc 

2
p
Per n> nc funzionam. da
generatore
Avviamento del motore
C em
Cr
L’avviam. corrisponde a
s=1. Inconvenienti:
• coppia bassa
• correnti elevate
(funzionam.nto analogo al
trasformat. in c.c.)
Se Cem < Cr motore non
spunta. Comunque una
bassa prevalenza di Cem
su Cr determina una %
Avviamento del motore
bassa accelerazione e un rallentamento
dell’avviamento. Una persistenza del motore intorno a
s=1 determina un riscaldamento eccessivo del motore e
una persistente caduta di tensione in rete. La corrente
assorbita, per quanto elevata, è però minore di quella del
trasformatore per s=1, perché è limitata dalle reattanze
di dispersione maggiori nel motore rispetto al
trasformatore a causa della maggiore dimensione del
traferro. I provvedimenti adottati sono diversi a seconda
del diverso tipo di avvolgimento rotorico.
Avviamento del motore a rotore
avvolto
C em
C em
r' R
Cr
C em
In tale motore è possibile
variare r’R inserendo un
reostato nell’avvolgim.
rotorico. Così aumenta
Cem e diminuisce IS in
avviam. (s=1). Aumenta
però anche s del
funzionamento ordinario
e quindi Pjr e diminuisce il
rendimento. Dopo
l’avviam. si disinserisce
gradualmente il reostato.
Avviamento del motore a rotore
avvolto
Avviamento del motore a gabbia
semplice
Non è possibile inserire un reostato nell’avvolgimento
rotorico. Se il motore è di piccola potenza è meno
importante il rendimento e si può aumentare r’R. Per
potenze maggiori, se il motore può partire a vuoto, si
può prescindere dal basso valore della coppia
d’avviamento, limitandosi a ridurre la corrente assorbita.
A tale scopo si può ridurre in avviamento la tensione di
alimentazione. Essendo Cem=f(V2) si ha una notevole
riduz. della coppia, per cui a motore avviato si riapplica
la piena tensione
Avviamento del motore a gabbia
semplice
C em
Per ridurre la tensione o si usa un commutatore
ΔY o si alimenta il motore con un variatore
elettronico di corrente. Se il motore non parte a
vuoto si può usare un motore a doppia gabbia.
Motore a doppia gabbia
e
i
gabbia
esterna
gabbia int erna
Induttanze di dispersione
 e ,  i linee medie dei tubi
di flusso di dispersione
concatenati con le barre
gabbie esterne e interne
Re , Ri riluttanze di tali tubi
di flusso (Re  Ri)
l  k / R  le  li
Resistenze
S e , S i sezioni barre
gabbie est. ed int.(S e  S i)
r  k ' / S  re  ri
Motore a doppia gabbia
Impedenze rotoriche
z r  rr  jsl
z r  zr  [rr2  (sl ) 2 ]
2
2
z

[
r

(
s

l
)
]
z re  [r  (sle ) ]
ri
i
i
2
e
2
Per s=1 z re  le , z ri  li  z re  z ri  la
IR si addensa nella gabbia esterna che ha una
caratteristica fortemente resistiva e quindi
determina una buona coppia di avviamento
Per s=sN z re  re , z ri  ri  z re  z ri  la IR
si addensa nella gabbia interna che ha una %
z ri  lie
Motore a doppia gabbia
caratterist. fortemente
induttiva e quindi una
forte pendenza
iniziale della curva
Cem-s ed un buon
rendim. a regime.
La coppia effettiva e
approssimativamente
data dalla somma
delle coppie relative a
ciascuna delle gabbie
Regolazione di velocità
Essendo la velocità di rotazione data da:
2f
 r  (1  s)c  (1  s)
p
per variare la velocità si può agire
• sullo scorrimento s,
• sul numero di coppie polari p,
• sulla frequenza f.
Regolazione di velocità variando lo
scorrimento
rR
s ' s' ' s' ' '
• Si ottiene inserendo una
resistenza variabile nel
rotore
• Possibile solo nel motore
a rotore avvolto
• A partire dalla caratt.
naturale si può solo
rallentare.
• Aumentando s peggiora il
rendim.to
• Perciò le variaz. di veloc.
sono modeste
Regolazione di velocità variando il
numero p delle coppie polari
• La variazione di velocità è discontinua ( ad es.
variando p da 1 a 2, n S passa da 3000 giri a
1500 giri al min.)
• Per variare p si può intervenire solo
sull’avvolgimento statorico, non essendo
possibile nel rotore modificare le connessioni
dell’avvolgim. a macchina in movimento.
• È possibile solo nel motore a gabbia , in cui
l’avvolgimento a gabbia adegua
automaticamente il suo numero di poli a quello
dell’avvolgimento statorico.
Regolazione di velocità variando la
frequenza di alimentazione
c
v2 , f 2
Re te
v1 , f1

La variaz. di f comporta
necessariamente anche
la variaz. della tensione di
alimentaz. del motore VS.
Sono possibili diverse
leggi di regolaz. VS=F(f).
Molto usata è la legge
VS/f=costante, adottata
per ottenere
approssimativamente la
costanza del flusso Φ. %
Regolazione di velocità variando la
frequenza di alimentazione
Infatti, trascurando la caduta di tensione nello statore la
LKT dello stesso è:
V S  jN S K ws 

VS  2fN S K ws 
VS
 f  2N S K ws   K
la costanza di VS/f comporta pertanto la costanza di Φ e
quindi della coppia massima, poiché:
k VS2
k
VS / f 2
C Max 

f x' R 2l 'R
per basse freq. non si può trascurare la caduta di
tensione nello statore
Motore asincrono monofase
Se non è disponibile
l’alimentaz. trifase, per
piccole potenze, da
decine di W fino a pochi
kW, è possibile l’uso del
motore monofase,
costituito da un rotore a
gabbia e da uno statore
monofase. Questo si può
ad es. ottenere
collegando in serie due
fasi di un mot. trifase. %
Motore asincrono monofase
Se tale mot. trifase ha un
avvolgim. trifase
distribuito sulla superficie
interna dello statore, 2/3
di tale superficie saranno
occupati dall’avvolgim.
principale monof. del mot.
monof. L’altro terzo potrà
essere occupato da un
avvolgim. ausiliario utile
per l’avviam. del motore.
Motore asincrono monofase, il
campo magnetico pulsante
L’avvolgim. monofase crea il campo pulsante:
B( , t )  BM cos t cos p
essendo:
1
cos( a) cos(b)  [cos( a  b)  cos( a  b)]
2
il campo pulsante è esprimibile come somma di
due campi Bd e Bi di ampiezza metà e rotanti in
verso opposto con velocità  ωc (ωc= ω/p).
1
B(  , t )  Bd  Bi  BM [cos( p  t )  cos( p  t )]
2
Scorrimenti rispetto al campo
diretto Bd e inverso Bi
Bi
 c
Bd
r
c
c   r
sd 
c
 c   r c   r
si 

 c
c
Il rotore, rotante con
velocità +ωr, presenta lo
scorrim. sd rispetto al
campo diretto Bd rotante
con veloc.  c e rispetto al
campo inverso Bi, rotante
con veloc.  c , lo scorrim.
si. La relaz. tra sd e si è:
s d  si  2
Assumendo come
scorrim. principale s lo
scorrim. sd, si ha:
si  2  s
Il motore asincrono monofase, la
caratteristica elettromeccanica
Sul rotore agiscono la
“coppia diretta” Cd creata
da Bd concorde con  r e
la “coppia inversa” Ci
creata da Bi opposta a  r.
Trascurando le interazioni
tra Bd e Bi:
C  Cd  Ci C d  Cem (s) / 3
dove C em è la coppia di
un mot. trif. con lo stesso
Ns del mot. monof. e:
Cem (si )
Ci  
 Cd (2  s)
3
Avviamento del motore monofase
La coppia d’avviam. (s=1) è nulla, poichè i due
campi diretti ed inversi si equilibrano. Se il
motore è avviato con veloc. ωr prevale il campo
concorde con ωr. Il motore può essere avviato
meccanicamente oppure elettricam. creando un
campo rotante. Non essendo possibile creare un
campo rotante trifase creato da un sistema
simmetrico trifase di correnti, si può ricorrere ad
un campo bifase creato dagli avvolgim.
principale ed ausiliario.
Campo bifase
Il campo è creato dagli avvolgimenti principale ed
ausiliario, i cui assi magnetici sono ortogonali e che
sono attraversati dalle correnti ip ed ia :
i p  I M cos t
ia  I M sin t
Se p=1
Campo principale
B p  BM cos  cos t
Campo ausiliario
Ba  BM sin  sin t
Campo risultante
B  BM cos(  t )
Motore monofase a condensatore
V
Ia
Ip
Motore a poli tagliati
Configuraz. motore trifase
Motore trifase
Motore asincrono monof. (p=1)
Motore asincrono monof. (p=2)