L`errore di quantizzazione.

Il Convertitore Digitale – Analogico ( DAC )
• Il convertitore digitale-analogico è un componente elettronico utilizzato per
convertire dati numerici codificati in forma binaria in segnali elettrici.
• Il convertitore DAC accetta in ingresso un numero binario ad es. un codice
numerico con otto ingressi e fornisce all’uscita una tensione ad esso
proporzionale
• In pratica sarà in grado di produrre una determinata differenza di
potenziale in funzione di un valore numerico che viene caricato all’ingresso;
Es: ad un valore pari ad 00000001 corrisponderà una tensione di uscita di
0,1 Volt,
ad un valore di 00000010 avremo 0,2 Volt e così via.
• Si definisce risoluzione la distanza tra un livello e l’altro ed è indicata da
una costante di proporzionalità detta Quanto di tensione q dove: (con 8 bit
in ingresso)
q=VFS/256
con VFS = tensione massima (Fondo Scala) in uscita
Il Convertitore Digitale – Analogico ( DAC )
• Si inizia dalla tensione massima o di fondo scala o di riferimento che
viene applicata esternamente e viene divisa ripetutamente per 2
mediante blocchi divisori
• Tutti i segnali vengono condotti ad un blocco sommatore e il valore
della tensione in uscita sarà proporzionale al numero binario in
ingresso.
Bit alto=1 -> chiusura del circuito -> passaggio del segnale VFS / 2n
Bit basso=0 -> apertura del circuito -> il segnale viene bloccato
Vediamo uno schema realizzativo per determinare la relazione che lega ingresso e
uscita ed evidenziare le differenze tra caso reale e ideale. Esempio a 8 bit
Chiuso se b7=1
Vfs
Vfs/2
:2
Chiuso se b6=1
Vfs/4
:2
Vfs/8
Chiuso se b5=1
:2
…
Vfs/256
:2
Chiuso se b0=1
S
O
M
M
A
Vout
Significato e importanza del quanto q
• Il quanto q è una costante di proporzionalità che
rappresenta il valore minimo di tensione che può costituirsi
all’uscita del DAC.
• q rappresenta anche l’intervallo di tensione tra due livelli
digitali successivi
• Nella conversione la tensione di uscita varierà non in modo
continuo (caso ideale) ma in modo discreto
• q indica l’accuratezza della conversione, detta anche
risoluzione del DAC:
q piccolo  maggiore risoluzione
Significato e importanza del quanto q
• Esempio: si vuole convertire un range di tensione da 0 a
10,24Volt con 8 bit
si avranno dei gradini di tensione pari a
10,24 / 256 = 40 mV
quindi una risoluzione q = 40 mV
• All'aumentare della risoluzione, però, corrisponde un
maggior numero di elaborazioni per ottenere la tensione
d'uscita; in altre parole, più è elevata la risoluzione del
DAC e più la sua elaborazione ne risulterà rallentata.
• La scelta della risoluzione dovrà obbligatoriamente
tenere conto della velocità del dispositivo impiegato,
rispetto all'utilizzo al quale è destinato.
Digitale  Analogico
Analogico  Digitale
Il Convertitore Analogico - Digitale ( ADC )
• Il convertitore analogico-digitale (Analog to Digital Converter ) è un
componente elettronico in grado di convertire i valori continui di un segnale
d’ingresso analogico v(t) in valori digitali (numeri binari) effettuando un
campionamento del segnale stesso.
• Per effettuare la conversione occorre un certo tempo detto
Tempo di conversione Tconv
• Al convertitore ADC non affluiscono direttamente i valori del segnale ma i valori
del segnale dopo il campionamento o meglio i valori del segnale mantenuto a una
tensione y(t)
• La corrispondenza fra i valori analogici y(t) e le cifre binarie in uscita è definita
come caratteristica del convertitore.
•Quanto (passo) q=VFS / 2R R = numero di uscite digitali o risoluzione del ADC
N.B. Il tempo di conversione deve essere inferiore al tempo di campionamento
in modo che nel tempo di attesa tra l’arrivo di un campione e il successivo, il
convertitore ha il tempo per la conversione del segnale.
Il Convertitore Analogico - Digitale ( ADC )
Risoluzione
La risoluzione di un convertitore indica il numero di valori discreti che può produrre.
È usualmente espressa in bit. Per esempio, un ADC che codifica un ingresso
analogico in 256 livelli discreti ha una risoluzione di 8 bit, essendo 28 = 256.
La risoluzione può anche essere definita elettricamente, ed espressa in volt.
La risoluzione in volt di un ADC è uguale alla minima differenza di potenziale tra due
segnali che vengono codificati con due livelli distinti adiacenti.
Esempio 1:
Range compreso tra 0 e 10 volt
Risoluzione dell'ADC di 12 bit:
212 = 4096 livelli di quantizzazione
La differenza di potenziale tra due livelli adiacenti è:
10 V / 4096=0.00244 V = 2.44 mV
Esempio 2:
Range compreso tra -10 e 10 volt
Risoluzione dell'ADC di 14 bit: 214 = 16384 livelli di quantizzazione
La differenza di potenziale tra due livelli adiacenti è:
20 V / 16384=0.00122 V = 1.22 mV
Il Convertitore Analogico - Digitale ( ADC )
• Accuratezza
• L'accuratezza dipende dall'errore della conversione.
Questo errore è formato da due componenti: un errore di quantizzazione e un
errore di non-linearità.
Questi errori sono misurati con un'unità chiamata LSB (least significant bit = bit
meno significativo) ed indica fino a che punto i bit rappresentano segnale e quanti
siano solo rumore.
• Esempio: In un ADC a 8 bit, un errore di 1 LSB è pari ad un errore di 1 / 256
ossia circa del 0.4%; è un modo per dire che l'ultimo bit è causale.
In un ADC a 16 bit con un errore di 4LSB significa che soli 12 bit rappresentano
segnale e gli ultimi 4 sono eliminabili senza perdita di informazione.
• L'errore di quantizzazione è dovuto alla risoluzione finita dell'ADC ed è una
imperfezione intrinseca di tutti i tipi di ADC. La grandezza dell'errore di
quantizzazione su un campione è compresa tra zero e un LSB.
Tutti gli ADC soffrono di errori di non-linearità causati da imperfezioni fisiche,
facendo deviare la loro l'uscita da una funzione lineare (o da un'altra funzione, in
caso di ADC volutamente non-lineari). Questi errori possono a volte essere
attenuati con una calibrazione.
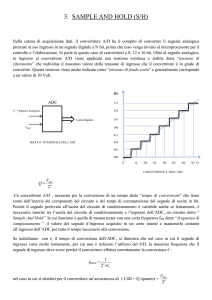
Un problema che riguarda gli ADC è legato al fatto che la conversione del
dato in formato digitale prevede un tempo di conversione finito tC per cui per
un corretto funzionamento del circuito si suppone che il valore di tensione
rimanga costante per il periodo indicato.
• All’atto pratico a monte del circuito quantizzatore si pone un sample & hold
in modo da convertire un valore fisso campionato ad un dato istante.
V
N
VC
S&H
QUANTIZZATORE
M
CODIFICATORE
BINARIO
• Occorre che sia verificato il teorema del campionamento di Shannon per
evitare la perdita di informazioni.
f C  2 fS max
N.B. Tempo di conversione< Tempo di campionamento
In questo caso occorre che il clock digitale sia molto veloce rispetto alle variazioni
della forma d’onda da convertire altrimenti si può verificare una perdita dell’aggancio
e ciò che risulta è che i dati digitali non sono più rappresentativi della forma d’onda
in ingresso.
Indicando con Ts il tempo di conversione e Tc il tempo di
Campionamento occorre avere
Ts  Tc
Interfacciamento tra ADC ed elaboratore
• Un convertitore analogico digitale può essere gestito
via software inviandogli gli opportuni controlli e
prelevando, dalle otto linee dei dati, il dato digitale
convertito.
• E’ necessario, per questo, interfacciare il convertitore
al sistema di elaborazione, realizzando un
collegamento fisico(hardware) tra le linee interne del
sistema di elaborazione e i terminali del convertitore
coinvolti nel processo.
Catena per l’acquisizione dei dati analogici
Trasduttore
Condizionatore
filtro
mux
S/H
A/D
CPU
Conversione analogico - digitale - La qualità della conversione..
Segnale in forma
numerica + errore
di quantizzazione
Vin
ADC
DAC
8 bit
Segnale
8 bit  28=256 livelli Esempio:
analogico dal
• Vin max=3 Volt => Risoluzione 3/256 = 0.01Volt
trasduttore
• Vin max=10Volt => Risoluzione 10/256 = 0.04Volt
Vmax / 2n : intervallo di quantizzazione
Segnale analogico
ricostruito dal DAC
intervallo di
quantizzazione
Dove n è il numero di bit del campionatore
Con risoluzione maggiore di 8 bit avremmo ottenuto un risultato affetto da minor errore!
Sull’asse delle ascisse è riportata la tensione analogica d’ingresso
mentre sull’asse delle ordinate è riportato il codice generato in uscita
Errore: Q(1/2).LSB (least significant bit )
4 bit
ADC
Conversione
A/D a 4 bit
Conversione A/D a 8 bit
Ad esempio al terzo “intervallo di clock” del campionatore, viene estratto un campione
pari a 2,6 Volt, che nel blocco successivo viene associato al codice 00..011. Si noti
l’errore di quantizzazione effettuato!
Schema minimo funzionale dell’ ADC
•
ADC
Vref+
Do
D1
Y(t)
…
DR-1
Vref-
START
EC
OE
Il costo di un convertitore AD è determinato da due parametri: la
massima frequenza di campionamento e il numero di bit per parola
(cioè la risoluzione).
Con la conversione D/A il segnale digitale è convertito in analogico.
Maggiormente
evidente
risulta
l’errore
introdotto
dalla
quantizzazione.
Fine
Un convertitore analogico digitale ADC svolge principalmente due
funzioni:
• Quantizzazione del segnale di ingresso
• Codifica in un segnale digitale il valore quantizzato
N
V
QUANTIZZATORE
M
CODIFICATORE
BINARIO
Il quantizzatore misura V mediante una quantità VQ detta passo di quantizzazione e
in uscita fornisce l’intero più prossimo al rapporto V/ VQ.
Il valore quantizzato VN viene poi convertito da un’apposita logica in
formato digitale a M bit.
Esempio:
Supponiamo un convertitore a 2 bit con una dinamica in ingresso da 0-4V.
• avremo una suddivisione in intervalli
come quella rappresentata in figura.
• il passo di quantizzazione risulta:
VQ 
4
 1V
2
2
• il VMAX rappresentabile risulta
(diversamente da VFS)
VMAX  VFS 
VQ
2
 3,5V
Un altro problema che riguarda gli ADC è legato al fatto che la conversione
del dato in formato digitale prevede un tempo di conversione finito tC per cui
per un corretto funzionamento del circuito si suppone che il valore di tensione
rimanga costante per il periodo indicato.
• All’atto pratico a monte del circuito quantizzatore si pone un sample & hold
in modo da convertire un valore fisso campionato ad un dato istante.
V
N
VC
S&H
QUANTIZZATORE
M
CODIFICATORE
BINARIO
• Occorre che sia verificato il teorema del campionamento di Shannon per
evitare la perdita di informazioni.
f C  2 fS max
In questo caso occorre che il clock digitale sia molto veloce rispetto alle variazioni
della forma d’onda da convertire altrimenti si può verificare una perdita dell’aggancio
e ciò che risulta è che i dati digitali non sono più rappresentativi della forma d’onda
in ingresso.
Il valore del passo di quantizzazione è legato all'ampiezza dell'intervallo,
cioè è funzione del numero di bit d'uscita e della tensione di fondo scala VFS.
VFS
VQ  M
2
Minore è il passo di quantizzazione e minore è l’errore associato al processo
di quantizzazione. Ad una tensione V analogica viene infatti associato un
valore VN. di uscita
V  VN  N  VQ
Schema realizzativo del DAC
÷2
÷2
Questo è uno
schema
realizzativo, utile
per determinare
l’espressione
matematica che
lega l’ingresso e
l’uscita ed
evidenziare le
principali
differenze tra
caso reale e
ideale.
chiuso se b7 = 1
VFS/2
chiuso se b6 = 1
VFC/4
÷2
VFC/8
chiuso se b5 = 1
Vout
SOMMA
VFS
...
VFS/256
÷2
chiuso se b0 = 1
Sampling rate
• Il segnale analogico è tempo-continuo ed è necessario
convertirlo in un flusso di valori discreti
• L'idea chiave è che un segnale di banda limitata che varia
con continuità può essere campionato e poi riprodotto
ESATTAMENTE dai valori tempo discreti con un
algoritmo di interpolazione se la frequenza di
campionamento è almeno pari al doppio della banda del
segnale (Legge di Shannon). L'accuratezza tuttavia è
limitata dall'errore di quantizzazione
• È quindi necessario definire una frequenza alla quale
campionare i valori discreti del segnale analogico. Questa
frequenza è chiamata sampling rate (frequenza di
campionamento, in italiano) del convertitore.
Aliasing
• Tutti gli ADC lavorano campionando il
proprio input ad intervalli discreti di tempo
L'output di conseguenza è un'immagine
incompleta dell'input e non c'è modo di sapere,
guardando soltanto l'output, che valori abbia
assunto l'input tra due istanti di campionamento
adiacenti
Il convertitore A/D (ADC).
• L’ADC trasforma un segnale analogico in un codice
binario Il passaggio da un segnale, che assume con
continuità tutti i valori all’interno di un intervallo, ad una
successione discreta di codici binari avviene tramite
un’operazione denominata quantizzazione.
La quantizzazione.
La quantizzazione è descritta dal graico seguente detto: caratteristica di
trasferimento.
• I valori di tensione in ingresso sono riportati sull’ascissa, mentre
sull’ordinata viene riportato il codice binario associato ad ogni intervallo
di valori di Vi.
• l’ampiezza massima del segnale d’ingresso è
VMax = 8 V. Il numero di
bit scelto è 3 quindi il numero possibile di codici binari esprimibili è
• Q = 23 = 8
• La tensione analogica d’ingresso è stata divisa in 8 parti
uguali, ad ognuna delle quali è stato associato uno degli
8 codici binari possibili.
• A tutti i valori di tensione appartenenti ad un singolo
intervallo degli otto possibili viene associato lo stesso
codice.
Parametri di un ADC
• Il primo è l’ampiezza massima VMax del segnale d’ingresso
che può essere convertito dall’ADC. Il segnale da
elaborare deve dunque passare prima in un circuito per
renderlo utilizzabile dal convertitore (condizionamento) .
• In particolare i campi di valori della Vi accettati dagli ADC
in commercio sono generalmente da 0 V a 5 V oppure
da 0 V a 10 V.
• L’altro parametro è il numero n di bit con cui si effettua la
codifica. Il campo dei valori della Vi viene diviso in
Q
= 2n parti uguali.
• Ad ognuno di questi 2n intervalli viene associata un
insieme di n bit (parola).
• L'ampiezza dell'intervallo è indicata come quanto oppure
passo di quantizzazione.
Parametri di un ADC
• La risoluzione, indicata con R, rappresenta la variazione della
tensione d’ingresso associata ad una variazione del bit meno
significativo del codice binario.
• La risoluzione rappresenta anche il passo di quantizzazione. In
effetti, come viene mostrato dall’esempio precedente, se il codice
binario differisce per il bit meno significativo (LSB), otteniamo
quello associato all’intervallo successivo o precedente. Possiamo
così scrivere:
ViM ViM
R
 n
Q 2
• Spesso i costruttori forniscono come risoluzione il numero di bit
utilizzati nella codifica.
L’errore di quantizzazione.
• L’errore di quantizzazione, indicato
anche come incertezza, definisce il livello
di indeterminazione ed è dovuto al fatto
che ad ogni codice binario non viene
associato un unico valore della tensione
d’ingresso ma l’insieme dei valori
appartenenti al passo di quantizzazione.
L’errore di quantizzazione.
• Ad esempio la figura 9 mostra che alla parola di
codice 010 sono associati tutti i valori della Vi
compresi tra 2 V e 3 V e di conseguenza 010
rappresenta oltre al valore esatto 2 V anche 2.9
V.
• Quando il valore esatto di Vi rappresentato dalla
parola di codifica è l’estremo inferiore
dell’intervallo, l’errore massimo di
quantizzazione (eM)
• è pari l’ampiezza dell’intervallo stesso (ossia alla
risoluzione R) e quindi:
• eM = R
L’errore di quantizzazione.
• Esempio se eM = 1 V.
l’andamento dell’errore in funzione del valore della tensione
è il seguente:
eM 
R
2
L’errore di quantizzazione.
• Si osserva che e = 0 quando in ingresso è
presente il valore esatto della tensione
associato alla parola binaria.
• Se il valore esatto di Vi rappresentato
dalla parola di codice è al centro
dell’intervallo di quantizzazione l’errore
massimo che si può commettere
• viene dimezzato:
R
eM 
2
L’errore di quantizzazione.
• In effetti se si sceglie il passo di quantizzazione in modo
che la parola 010 rappresenti l’intervallo di valori 1.5 V
2.5 V, simmetrico intorno al valore esatto 2 V, l’errore
massimo vale 0.5 V
• l’andamento dell’errore è il seguente:
• Per ridurre l’incertezza occorre diminuire l’ampiezza del
passo di quantizzazione aumentando il numero di bit.
Il tempo di conversione
• Il tempo di conversione è il tempo necessario
all’ADC per trasformare il valore della tensione
d’ingresso in un codice binario.
• Il segnale analogico da convertire deve essere
campionato per prelevare i valori della Vi da
trasformare in codice binario.
• Con il campionamento il segnale analogico
viene trasformato in una successione discreta di
valori di Vi
Esempio:
• Il segnale S(t) può essere rappresentato dalla successione dei suoi cam-pioni S1,
S2, S3, S4, S5 … prelevati ad intervalli regolari Tc. Il valore di Tc non può essere
qualsiasi. Per poter ricostruire il segnale dai suoi campioni
1
f

occorre che la frequenza di campionamento:
c
soddisfi la condizione di Shannon:
fc  2fM
dove fM è la frequenza massima (o banda) del segnale.
Di conseguenza il periodo di campionamento di Tc deve essere:
Tc
Tc 
1
2fM
Il tempo di conversione
• La conversione deve terminare prima che arrivi il nuovo campione
da con-vertire in codice binario.
• Indicando con Ts il tempo di conversione occorre avere
Ts  Tc
Il tempo di conversione
• Il valore del campione è quello assunto da Vi
all’inizio della conversione anche se durante il
tempo Ts il segnale subisce delle variazioni.
• Per non introdurre un ulteriore errore, il codice
binario associato al campione deve rimanere
valido per tutto il tempo di conversione.
• Di conseguenza le variazioni del segnale,
durante Ts, devono essere tali da fare rimanere
Vi all’interno del passo di quantizzazione (o
entro la risoluzione).
Il tempo di conversione
• Per lavorare con frequenze più elevate è
necessario inserire un dispositi-vo detto di
sample/hold (campionamento e mantenimento).
• In effetti se il tempo di conversione è alto a Tc,
c’è il rischio di perdere il nuovo campione
perché la conversione precedente non è
terminata.
• Per evitare ciò il valore viene memorizzato
(hold) fino a quando deve essere convertito.